Dans cet article, vous trouverez la définition du théorème de Weierstrass. De plus, vous pourrez vous entraîner avec plusieurs exercices résolus pas à pas du théorème de Weierstrass pour le comprendre parfaitement.
Énoncé du théorème de Weierstrass
Le théorème de Weierstrass dit que si une fonction est continue sur un intervalle fermé, cette fonction a un maximum absolu et un minimum absolu sur cet intervalle.
➤ Voir : Qu’est-ce qu’une fonction continue ?
Le théorème de Weierstrass établit seulement qu’il y a un maximum et un minimum, mais il n’est pas utile de calculer les valeurs de ces points.
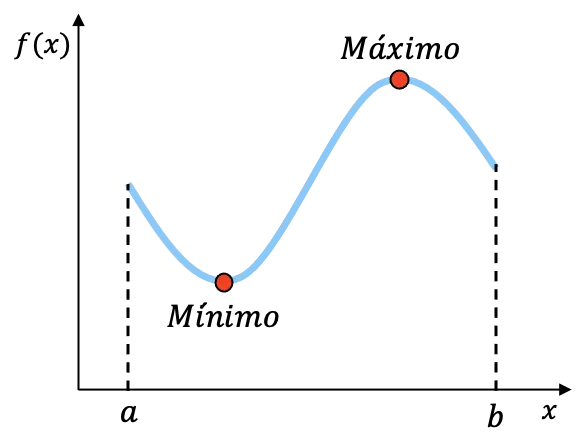
Par exemple, la fonction représentée graphiquement ci-dessus est continue sur l’intervalle [a,b] et a un minimum et un maximum sur cet intervalle. Bien que nous ne puissions pas connaître exactement les coordonnées de ces deux points, nous savons que la fonction a ces deux extrémités dans l’intervalle.
➤ Voir : comment calculer le maximum et le minimum d’une fonction
Puisque la fonction est continue sur tout l’intervalle, cela signifie qu’elle prendra également toutes les valeurs possibles entre le minimum absolu et le maximum absolu sur ce même intervalle.
De plus, comme conséquence du théorème de Weierstrass, on peut déduire que toute fonction continue sur un intervalle fermé est bornée au-dessus et au-dessous de , et les bornes supérieure et inférieure de la fonction sont respectivement le maximum et le minimum absolus.
Mathématiquement, le théorème de Weierstrass peut être exprimé comme suit :
Où
et
sont deux points inclus (le minimum absolu et le maximum absolu respectivement) dans l’intervalle fermé![[a,b]](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcda5ef4ae327e1afef79dc73df91703_l3.png "Rendered by QuickLaTeX.com")
dans lequel la fonction est définie.
La preuve du théorème de Weierstrass est assez compliquée et ne contribue pas beaucoup au concept, nous ne l’expliquerons donc pas dans cet article. L’important est que vous compreniez ce qu’est le théorème de Weierstrass et à quoi il sert.
Problèmes résolus du théorème de Weierstrass
Exercice 1
Déterminez si la fonction suivante est bornée sur l’intervalle proposé :
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e6a705ea1c5d586cf31d683ac7ccc85_l3.png "Rendered by QuickLaTeX.com")
➤ Voir : domaine d’une fonction logarithmique
On peut déterminer si la fonction est bornée sur l’intervalle [5,10] en appliquant le théorème de Weierstrass. Il faut donc savoir si la fonction est continue dans cet intervalle, pour cela, on calcule le domaine de la fonction logarithmique :
La fonction est continue pour toutes les valeurs supérieures à x=4, donc elle est continue sur l’intervalle [5,10].
Par conséquent, la fonction satisfait le théorème de Weierstrass sur l’intervalle [5,10], ce qui signifie qu’elle est bornée en haut et en bas sur cet intervalle.
Exercice 2
Déterminez si la fonction suivante a un maximum et/ou un minimum sur l’intervalle proposé :
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f2e72f629bae2c39821ddbfbf6c93fc_l3.png "Rendered by QuickLaTeX.com")
➤ Voir : domaine d’une fonction rationnelle
Premièrement, nous analysons la continuité de la fonction rationnelle :
Cependant, la fonction présente une discontinuité en x=2, ce qui implique qu’elle n’est pas continue sur l’intervalle [-3,3].
En bref, la fonction ne satisfait pas le théorème de Weierstrass et nous ne pouvons donc pas dire si elle a un minimum ou un maximum dans cet intervalle.
Exercice 3
Déterminez si la fonction suivante a un maximum et/ou un minimum dans l’intervalle proposé et calculez ces points :
![f(x)=x^2+3 \qquad x \in [0,4]](https://mathority.org/wp-content/ql-cache/quicklatex.com-4dd0cf4151f8b5c1b4e69be89b7a71e1_l3.png "Rendered by QuickLaTeX.com")
➤ Voir : caractéristiques des fonctions quadratiques
Le domaine de toute fonction quadratique est tous les nombres réels :
La fonction est donc continue sur l’intervalle [0,4] et vérifie le théorème de Weierstrass. La fonction a donc un minimum absolu et un maximum absolu sur cet intervalle.
De plus, le sommet de cette parabole est exactement en x=0, donc la fonction est strictement croissante sur l’intervalle [0,4] et, par conséquent, le minimum se trouve en x=0 et le maximum en x= 4.
Karl Weierstrass
Une fois que nous aurons vu ce que signifie le théorème de Weierstrass, nous allons brièvement expliquer qui était l’inventeur de ce théorème.
Karl Theodor Wilhelm Weierstrass était un mathématicien allemand très important au XIXe siècle, plus précisément, il est né le 31 octobre 1815 à Ostenfelde et mort le 19 février 1897 à Berlin.
En plus du théorème de Weierstrass, il est également connu pour ses autres contributions aux mathématiques. Parmi eux, il a donné les définitions de continuité, de limite et de dérivée, trois concepts très importants de fonctions.
De même, il a réussi à démontrer certains théorèmes qui n’étaient pas encore vérifiés mathématiquement à cette époque, comme le théorème de Bolzano-Weierstrass, le théorème de la valeur moyenne ou le théorème de Heine-Borel.
Comme curiosité, il y a un cratère lunaire et un astéroïde nommé d’après Weierstrass en son honneur.