Fonction constante

Dans cet article, nous expliquons ce qu’est une fonction constante et quelle est sa représentation graphique. De plus, vous pourrez voir plusieurs exemples de fonctions constantes et toutes les caractéristiques de ce type de fonction. Et, enfin, vous pourrez vous entraîner avec des exercices résolus de fonctions constantes.

Qu’est-ce qu’une fonction constante ?

Une fonction constante est cette fonction qui prend toujours la même image pour toute valeur de la variable indépendante (x) , c’est-à-dire qu’une fonction constante est de la forme f(x)=k , où k est un nombre réel quelconque.

$f(x)=k$

La représentation graphique d’une fonction constante est une ligne horizontale.

Par exemple, toutes les fonctions suivantes sont des constantes :

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

Représentation graphique d’une fonction constante

Une fois que nous avons vu le concept de fonction constante, nous allons voir comment représenter une fonction constante dans un graphe.

Représenter graphiquement une fonction constante est assez simple, il suffit de tracer une ligne horizontale dans la valeur de la fonction (k).

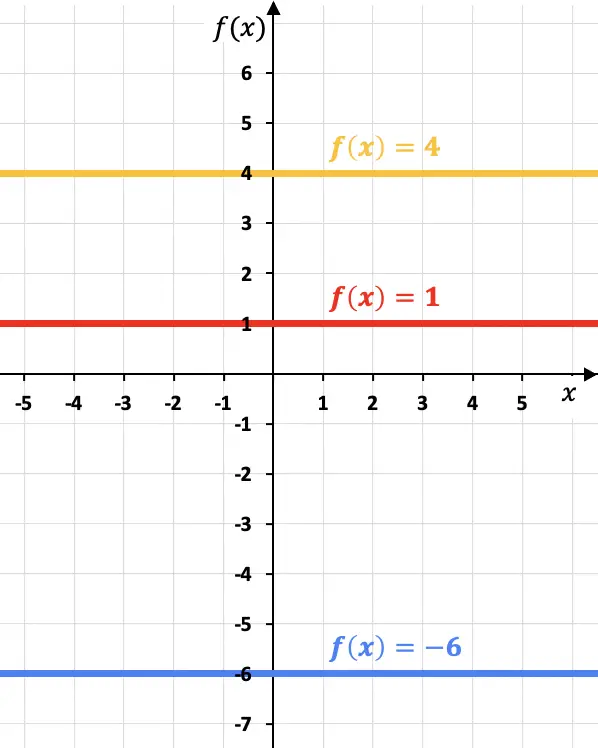
Regardez les exemples suivants dans lesquels nous avons représenté trois fonctions constantes différentes sur un graphique :

Notez que chaque fonction constante est parallèle à l’axe des abscisses (axe X).

D’autre part, vous devez garder à l’esprit qu’une ligne verticale n’est pas une fonction constante. En fait, une ligne verticale n’est même pas une fonction, puisque par définition une fonction ne peut avoir qu’une seule image pour chaque valeur de x.

Caractéristiques de la fonction constante

Ensuite, nous allons analyser les propriétés de la fonction constante. Soit une fonction constante de n’importe quelle valeur :

$f(x)=k$

Le domaine de la fonction constante est tous les nombres réels :

$\text{Dom } f = \mathbb{R}$

Le chemin ou la plage de la fonction constante est uniquement la valeur de la constante :

$\text{Im } f= k$

C’est une fonction continue et paire, car la fonction prend toujours la même valeur :

$\displaystyle f(x)=f(-x)$

La fonction constante n’est ni croissante ni décroissante, c’est un type de fonction qui a toujours une pente nulle :

$m=0$

Il coupe toujours l’axe OY au point (0,k).

$(0,k)$

Toute fonction constante est un polynôme de degré zéro.

Ouais 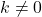$k\neq 0$ la fonction constante n’a pas de racine, à la place, si 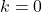$k=0$ tous les nombres réels sont les racines de la fonction constante.

La limite de la fonction constante lorsque x tend vers plus l’infini ou moins l’infini est égale à la valeur de la constante :

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

La dérivée de la fonction constante est toujours nulle :

$f(x)=k \ \longrightarrow \ f'(x)=0$

En fait, la définition de la fonction constante peut aussi se faire à partir de la notion de dérivée : une fonction est constante si sa dérivée s’annule sur tout son domaine.

L’intégrale de la fonction constante est la fonction linéaire (ou affine) :

$\displaystyle \int k \ dx= x + C$

➤ Voir : Qu’est-ce qu’une fonction linéaire ?

Fonction constante sur un intervalle

Nous avons vu comment est une fonction constante, cependant, une fonction ne peut être constante que dans un intervalle de son domaine.

Afin de comprendre ce concept, vous devez savoir quelles fonctions sont définies en morceaux, donc avant de continuer, nous vous recommandons de jeter un œil à l’explication suivante :

➤ Voir : Qu’est-ce qu’une fonction par morceaux ?

Une fois que vous savez quels sont ces types de fonctions, regardez la fonction définie dans les pièces représentées ci-dessous :

Comme vous pouvez le voir sur le graphique, la fonction n’est pas constante dans tous les nombres de son domaine. Mais elle est constante dans l’intervalle [-2,4), donc c’est une fonction constante uniquement dans un intervalle.

Problèmes résolus de la fonction constante

Exercice 1

Identifiez lesquelles des fonctions suivantes sont des constantes :

$f(x)=4\qquad g(x)=x+3\qquad h(x)=0\qquad z(x)=5x$

voir solution

La première fonction,

$f(x)=4$ , est une fonction constante puisqu’elle vaut toujours 4 quelle que soit la valeur que prend la variable x.

La deuxième fonction,

$g(x)=x+3$ , n’est pas une fonction constante car la valeur de la fonction varie en fonction de la valeur de x. C’est une fonction affine.

La troisième fonction,

$h(x)=0$ , est toujours égal à 0 pour toute valeur de x, il s’agit donc bien d’une fonction constante.

La quatrième fonction,

$z(x)=5x$ , n’est pas une fonction constante car elle varie en fonction de la valeur de x. C’est une fonction linéaire.

Exercice 2

Trouvez la fonction constante qui passe par le point (0,6).

voir solution

Algébriquement, la formule de la fonction constante a toujours la même forme :

$f(x)=k$

Et graphiquement la fonction constante est toujours une ligne horizontale, donc, les coordonnées d’une fonction constante sont toujours égales et de valeur

$k.$

Puisque le point par lequel passe la fonction a pour coordonnée y=6, la fonction constante que nous recherchons dans ce problème doit être :

$f(x)=6$

Exercice 3

Représentez les fonctions constantes suivantes sur le même graphique :

$f(x)=4\qquad f(x)=1\qquad f(x)=-6$

voir solution

Pour représenter chaque fonction constante, il suffit de tracer une ligne droite horizontale à la hauteur de chaque constante :

Qu’est-ce qu’une fonction constante ?

Représentation graphique d’une fonction constante

Caractéristiques de la fonction constante

Fonction constante sur un intervalle

Problèmes résolus de la fonction constante

Exercice 1

Exercice 2

Exercice 3

Leave a Comment Cancel Reply