Fonction linéaire et fonction affine -

Dans cet article, vous trouverez l’explication de la fonction affine et de la fonction linéaire, ainsi que les différences qui existent entre ces deux types de fonctions. De plus, vous verrez des exemples sur la façon de représenter graphiquement une fonction affine et une fonction linéaire et sur la manière de calculer leurs expressions à partir de deux points. Enfin, vous pourrez vous entraîner avec plusieurs exercices résolus étape par étape.

Qu’est-ce qu’une fonction affine et une fonction linéaire ?

Les définitions de la fonction affine et de la fonction linéaire sont les suivantes :

Une fonction affine est une fonction polynomiale du premier degré, c’est-à-dire une fonction qui, représentée sur le graphique, est une ligne droite. Les fonctions associées sont les suivantes :

$f(x)=mx+n$

Où

$m$ est la pente de la droite et $n$ C’est l’ordonnée à l’origine, c’est-à-dire là où la fonction coupe l’axe vertical.

En mathématiques, les fonctions affines sont également appelées transformations linéaires dans le contexte de l’algèbre linéaire.

Une fonction linéaire est une fonction affine qui n’a pas de terme indépendant. Par conséquent, la formule des fonctions linéaires est la suivante :

$f(x)=mx$

Où

$m$ est la pente de la droite.

Le domaine et l’étendue (ou l’étendue) de la fonction linéaire et de la fonction affine sont tous des nombres réels :

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Quelle est la différence entre une fonction linéaire et une fonction affine ?

Maintenant que vous avez vu les concepts de fonction linéaire et de fonction affine, vous aurez remarqué qu’elles sont très similaires les unes aux autres. Cependant, la différence suivante entre eux est très importante :

La seule différence entre la fonction linéaire et la fonction affine est que la fonction linéaire n’a pas de terme indépendant alors que la fonction affine a toujours le coefficient de l’ordonnée à l’origine (n) différent de zéro (0).

Fonction linéaire

$f(x)=mx$

fonction affine

$f(x)=mx+n$

Cela implique qu’une fonction linéaire passe toujours par l’origine des coordonnées , le point (0,0). En revanche, une fonction affine ne passera jamais par ce point car elle a une ordonnée à l’origine autre que 0.

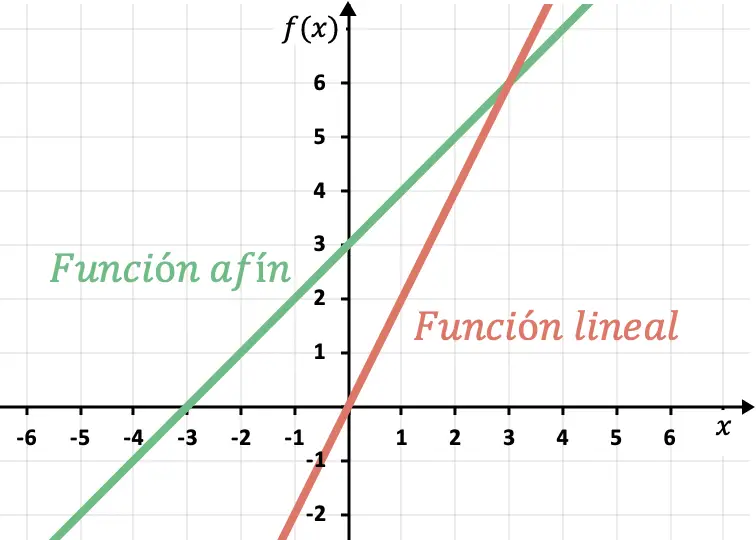
Quelle est la différence entre une fonction linéaire et une fonction affine ?

Pente et ordonnée à l’origine d’une fonction linéaire ou affine

Dans cette section, nous allons analyser un exemple de fonction affine ou linéaire pour comprendre la signification des termes

$m$ et $n$ , ou en d’autres termes, la pente et l’ordonnée à l’origine.

Déterminez l’expression de la fonction représentée sur le graphique et classez-la comme fonction linéaire ou affine.

Ces types de fonctions suivent l’expression suivante :

$f(x)=mx+n$

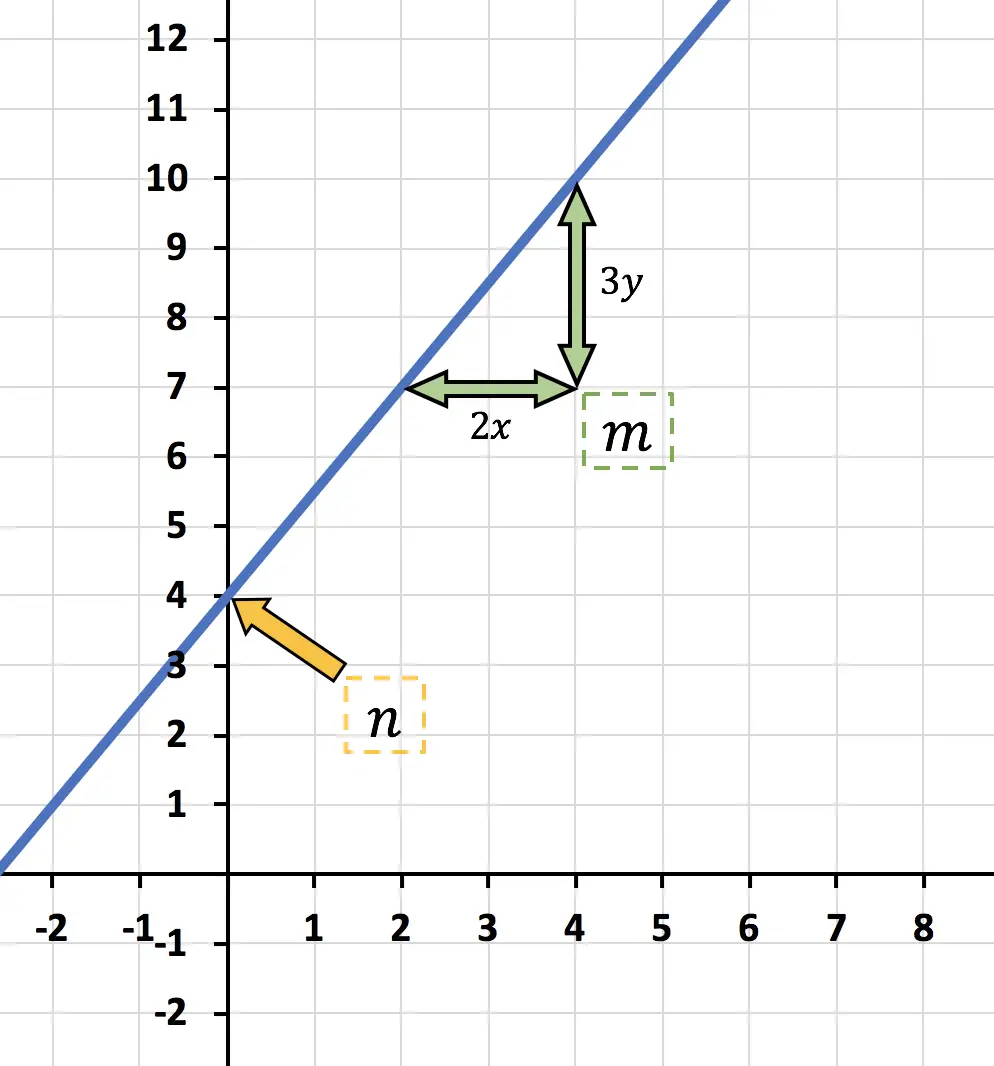
signifiant pente et ordonnée à l'origine fonction linéaire ou affine m et n

$n$ C’est l’ordonnée à l’origine, c’est-à-dire là où la fonction coupe l’axe vertical Y. Donc dans ce cas :

$n=4$

D’un autre côté,

$m$ est la pente de la droite. Y peut être calculé en divisant la différence de y entre deux points par la différence de x entre ces deux mêmes points :

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$ indique “combien de y augmente pour chaque x” , donc dans ce cas, la fonction “3y augmente pour chaque 2x” .

En conclusion, l’expression de la fonction affine représentée dans le graphique est :

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

De plus, comme l’ordonnée à l’origine est différente de zéro, c’est une fonction affine .

Ci-dessous, nous vous montrons d’autres exemples de fonctions linéaires et affines pour compléter votre compréhension :

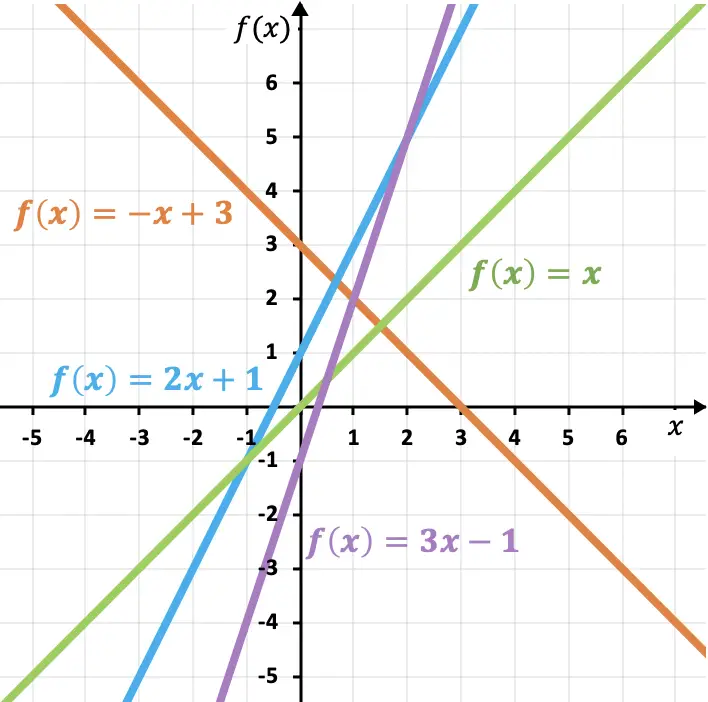
Comme vous pouvez le voir dans ces exemples, plus la pente est grande, plus la ligne est raide et, par conséquent, plus la fonction grandit. De même, le coefficient de pente détermine la croissance ou la diminution d’une fonction :

Si la pente est positive, la fonction est croissante , c’est-à-dire qu’elle croît à mesure que x augmente.
Si la pente est négative, la fonction est décroissante , c’est-à-dire qu’elle diminue à mesure que x augmente.

De plus, vous pouvez également savoir si deux droites sont parallèles ou perpendiculaires grâce à leurs pentes :

Lorsque deux droites ont la même pente, elles sont parallèles , c’est-à-dire qu’elles ne se coupent en aucun point ou sont complètement identiques.

$m_1 = m_2$

D’autre part, deux droites sont perpendiculaires , c’est-à-dire qu’elles se coupent selon un angle vertical (90º), si leurs pentes répondent à la relation suivante :

$m_1 = -\cfrac{1}{m_2}$

Exemple de représentation d’une fonction affine ou linéaire

Voyons comment représenter graphiquement une fonction du premier degré à l’aide d’un exemple.

Représentez la fonction affine suivante sur un graphique :

$f(x)=2x-1$

La première chose que nous devons faire est de créer un tableau de valeurs. Pour ce faire, nous accordons les valeurs que nous souhaitons

$x$ pour obtenir des valeurs de $f(x)$ :

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

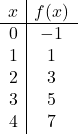
Bien qu’un tableau de valeurs avec deux points soit suffisant, nous pouvons faire plus de points pour nous assurer qu’il est correct.

Une fois que nous avons créé le tableau des valeurs, nous représentons les points sur le graphique :

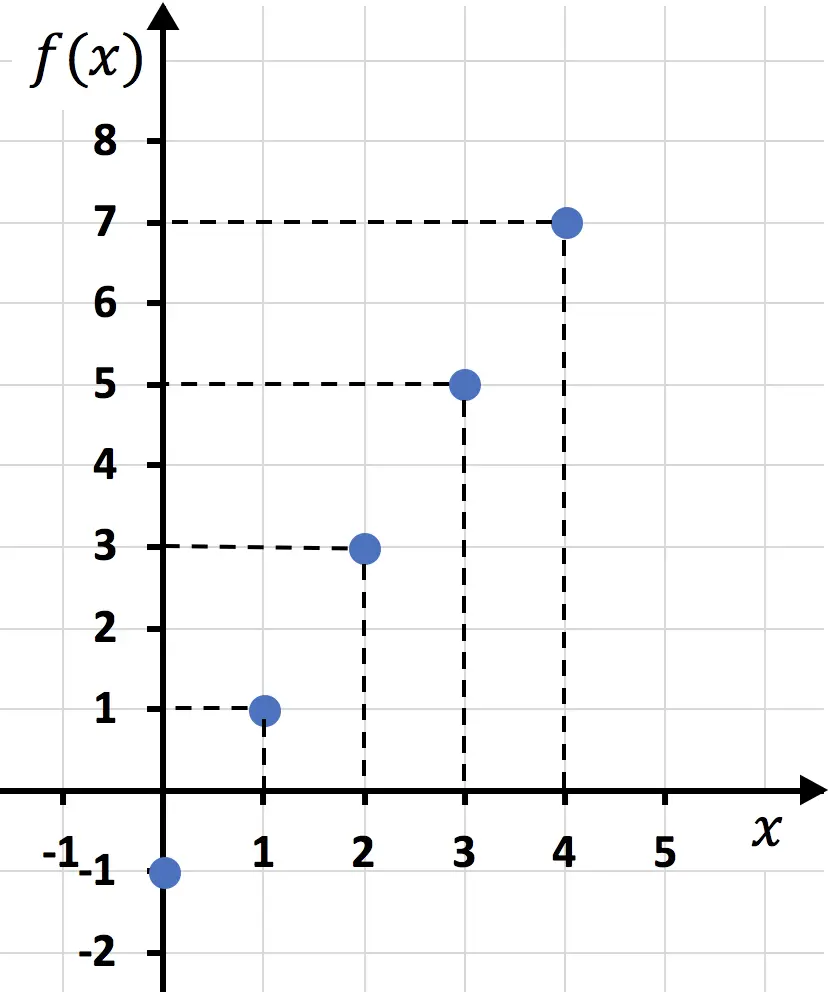
comment représenter une ligne ou une fonction linéaire ou et affine

Et enfin, nous joignons les points et traçons une ligne :

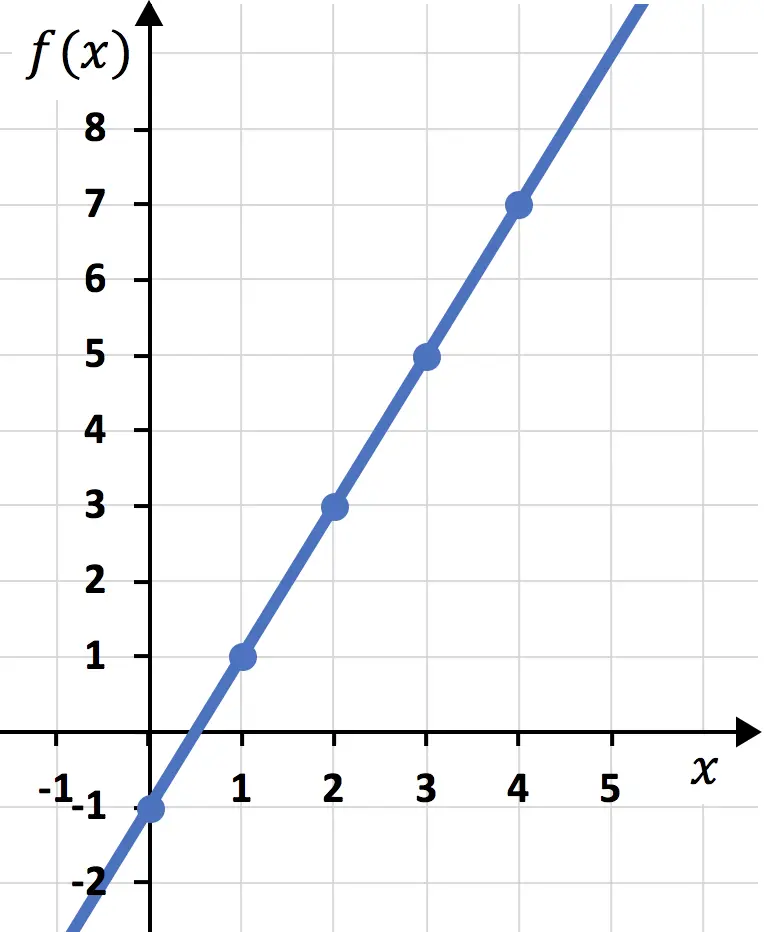
représentation graphique d'une fonction linéaire ou affine

Et de cette façon, nous avons déjà représenté la fonction sur un graphique. Comme vous pouvez le constater, ce n’est pas compliqué, il faut simplement d’abord faire un tableau de valeurs puis tracer les points sur un graphique.

Comment calculer une fonction linéaire ou affine à partir de deux points

Voyons maintenant comment trouver une fonction linéaire ou affine à partir de deux points à l’aide d’un exemple :

Calculer la fonction linéaire qui remplit 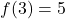$f(3)=5$ et passer par le point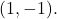 $(1,-1).$

Tout d’abord,

$f(3)=5$ Cela signifie que la fonction passe par le point $(3,5)$ .

Par conséquent, puisque nous avons deux points par lesquels passe la fonction, nous pouvons calculer la pente

$m$ de fonction :

Compte tenu de deux points,

$P_1=(x_1,y_1)$ et $P_2=(x_2,y_2)$ , pente $m$ de la fonction est calculé :

$m=\cfrac{y_2-y_1}{x_2-x_1}$

Dans notre cas la fonction passe par les points

$(3,5)$ et $(1,-1)$ . Donc la pente $m$ de la fonction est :

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

La fonction sera donc de la forme :

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Une fois que nous savons

$m$ nous pouvons résoudre le mystère $n$ . Pour ce faire, nous substituons dans l’équation les coordonnées d’un point appartenant à la fonction. Par exemple le point (3,5) :

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

On résout l’équation résultante :

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

La fonction linéaire est donc :

$\bm{f(x)=3x-4}$

Exercices résolus sur les fonctions linéaires et affines

Exercice 1

Déterminez la pente et l’origine de la fonction affine suivante :

$f(x)=-5x-2$

Voir la solution

Une fonction linéaire est de la forme

$f(x)=mx+n .$

La pente de la fonction est donc le nombre qui accompagne x , qui dans ce cas est -5 :

$\bm{m=-5}$

Et l’ordonnée à l’origine est le terme indépendant, qui dans ce cas est -2 :

$\bm{n=-2}$

Exercice 2

Représentez la fonction affine suivante sur un graphique :

$f(x)=x+1$

Voir la solution

Nous donnons d’abord des valeurs à

$x$ pour créer la table de valeurs :

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

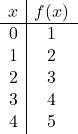
Et puis on représente les points du tableau de valeurs sur le graphique et on trace la ligne :

Exercice 3

Tracez la fonction affine suivante sur le graphique :

$f(x)=-2x+6$

Voir la solution

Nous donnons d’abord des valeurs à

$x$ pour créer la table de valeurs :

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

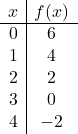
Et enfin nous représentons les points de la table de valeurs sur le graphique et traçons la ligne :

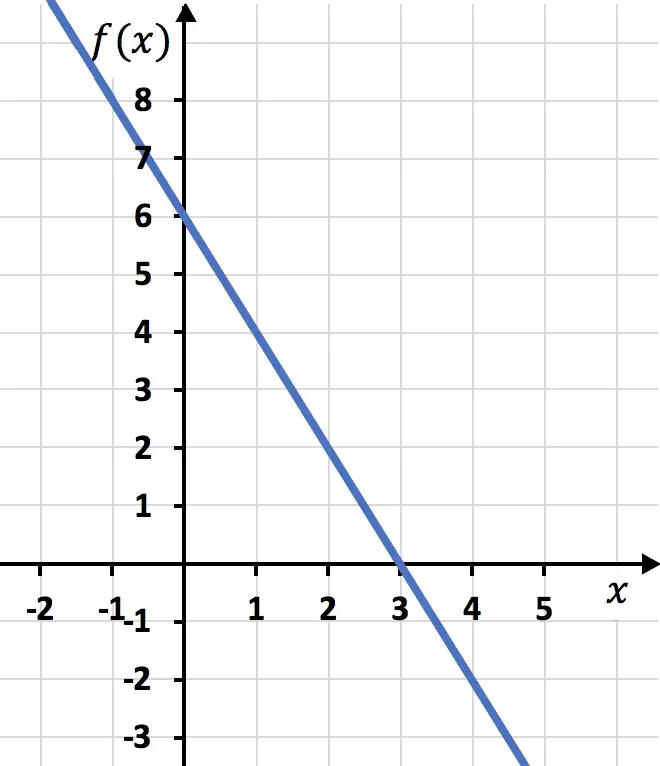
exercice résolu étape par étape de fonction linéaire et affine

Exercice 4

Trouver l’expression de la fonction affine qui passe par les points (2,3) et (0,1).

Voir la solution

La fonction passe par les points (2,3) et (0,1), donc la pente de la fonction est :

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

Et la fonction sera de la forme :

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Une fois que nous connaissons m, nous pouvons calculer n . Pour ce faire, nous devons substituer les coordonnées d’un point appartenant à la fonction dans l’équation. Par exemple le point (2,3) :

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$ $3=2+n$

Il faut maintenant résoudre l’équation résultante :

$3-2=n$

$1 = n$

La fonction correspond donc à l’expression suivante :

$\bm{f(x)=x+1}$

Exercice 5

Représentez graphiquement la fonction affine suivante :

$f(x)=2x-1$

Voir la solution

Nous donnons d’abord des valeurs à

$x$ pour créer la table de valeurs :

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

Et puis on représente les points du tableau de valeurs sur le graphique et on trace la ligne :

Exercices résolus pour représenter graphiquement une fonction linéaire ou affine

Exercice 6

Calculez la fonction linéaire qui satisfait les deux conditions suivantes :

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Voir la solution

Puisse-t-il s’accomplir

$f(3)=-2$ Cela signifie que la fonction passe par le point (3,-2). Et, de la même manière, $f(-1)=6$ Cela signifie que la fonction passe par le point (-1,6).

Donc la fonction passe par les points (3,-2) et (-1,6), donc sa pente est :

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

La fonction sera donc de la forme :

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

Et une fois que nous connaissons m, nous pouvons calculer n . Pour ce faire, on substitue les coordonnées d’un point qui appartient à la fonction dans l’équation. Par exemple le point (3,-2) :

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

Et on résout l’équation résultante :

$-2=-6+n$

$-2+6=n$

$4 = n$

La fonction est donc :

$\bm{f(x)=-2x+4}$

Exercice 7

Trouver la fonction affine qu’il remplit

$f(1) =6$ et passe par le point (3,5).

Voir la solution

Puisse-t-il s’accomplir

$f(1)=6$ Cela signifie que la fonction passe par le point (1,6).

La fonction passe donc par les points (1,6) et (3,5) et donc sa pente est :

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

La fonction sera donc de la forme :

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

Une fois que nous connaissons le terme m nous pouvons calculer le coefficient n . Pour ce faire, on substitue les coordonnées d’un point qui appartient à la fonction dans l’équation. Par exemple le point (1,6) :

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

On résout l’équation résultante :

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

N’oubliez pas que pour additionner des fractions, vous devez d’abord les réduire à un dénominateur commun puis additionner les numérateurs :

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

La fonction est donc :

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Exercice 8

Résolvez le problème suivant lié aux fonctions linéaires et affines :

Un magasin vend 40 unités d’un produit lorsque le prix est de 15 €/unité, et 65 unités lorsque le prix est de 10 €/unité.

Calculez la fonction de demande du produit, en supposant qu’il s’agit d’une fonction affine.
Combien d’unités seront vendues si le prix est fixé à 12€/unité ?

Voir la solution

Puisqu’il s’agit d’une fonction affine, la fonction sera du type

$f(x)=mx+n .$

Où

$x$ sera le prix unitaire du produit et $f(x)$ seront les unités vendues.

Le communiqué nous apprend que lorsque le prix est de 15 €/unité, 40 unités sont vendues. Par conséquent, comme

$x$ est le prix et $f(x)$ unités vendues, l’égalité suivante doit être respectée :

$f(15)=40$

Et lorsque le prix est de 10 €/unité, 65 unités sont vendues. Donc, en reprenant le même raisonnement :

$f(10)=65$

Puisse-t-il s’accomplir

$f(15)=40$ Cela signifie que la fonction passe par le point (15,40). ET $f(10)=65$ Cela signifie que la fonction passe par le point (10.65).

La pente de la fonction est donc :

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

La fonction sera donc de la forme :

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

Une fois que nous connaissons m, nous pouvons calculer n . Pour ce faire, on substitue les coordonnées d’un point qui appartient à la fonction dans l’équation. Par exemple le point (15h40) :

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$