Sur cette page vous trouverez tout sur les fonctions par morceaux : ce qu’elles sont, comment calculer leur image et leur domaine, comment les représenter sur un graphique, leur continuité, etc. De plus, vous verrez des exemples et vous pourrez vous entraîner avec des exercices résolus étape par étape de fonctions définies par morceaux.
Qu’est-ce qu’une fonction définie par morceaux ?
La définition d’une fonction définie par morceaux est la suivante :
En mathématiques, une fonction par morceaux est une fonction dont l’expression change en fonction de la valeur de la variable indépendante x.
Par exemple, la fonction suivante est définie en morceaux :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x+2 & \text{si} & x<1 \\[2ex] -2x+8 & \text{si} & x \geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-bce7bb676a634b5868c4299ed02693b6_l3.png)
Comme vous pouvez le voir, la fonction comporte deux sections différentes : si
![]() est inférieur à 1, la fonction sera
est inférieur à 1, la fonction sera![]() D’un autre côté, oui
D’un autre côté, oui![]() est supérieur ou égal à 1 la fonction sera valide
est supérieur ou égal à 1 la fonction sera valide![]()
Bien que ci-dessous nous verrons comment elles sont représentées, ci-dessous vous avez le graphique de cette fonction définie en morceaux :

Les fonctions définies en morceaux sont également appelées fonctions définies par parties ou morceaux, fonctions sectionnées, fonctions segmentées, fonctions multiparties, fonctions par intervalles,… entre autres.
Image d’une fonction définie par morceaux
Pour calculer l’image d’une fonction définie par parties il faut prendre l’expression de l’intervalle auquel appartient la variable.
Écrit ainsi, cela peut paraître très compliqué, mais avec un exemple vous verrez que c’est simple :
*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x+2 & \text{si} & x \leq 0 \\[2ex] 5 & \text{si} & 0 Cette fonction définie par morceaux signifie que si
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Please use \mathaccent for accents in math mode.
leading text: ...[2ex] 5 & \text{si} & 0 Cette fonction dé
\begin{array} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Emergency stop.
x![]() x+2
x+2![]() x=0
x=0![]() x=4
x=4![]() x=4
x=4![]() 2x^2-4.
2x^2-4.![]() f(-3)
f(-3)![]() x\le0
x\le0![]() f(-3)=-3+2=-1
f(-3)=-3+2=-1![]() f(2)
f(2)![]() 0 , parce que
0 , parce que![]() est dans cette plage :
est dans cette plage :
![]()
Et si nous voulons trouver
![]() nous devons le faire avec la dernière expression, puisque
nous devons le faire avec la dernière expression, puisque![]() appartient à cet intervalle :
appartient à cet intervalle :
![]()
Domaine d’une fonction définie par morceaux
Le domaine d’une fonction définie en sections est l’union des différents sous-domaines associés à chacune de ses branches.
Par exemple, pour déterminer le domaine de la fonction suivante définie par intervalles il faut calculer le domaine de chaque sous-fonction :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3x+1 & \text{si} & x\leq 2 \\[2ex] \cfrac{3}{x-5} & \text{si} & x>2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c1dcf2ec8fc15a629fa0b0b988fe8ef_l3.png)
La première section est une fonction polynomiale, donc son domaine est constitué de nombres réels (jusqu’à x=2).
![]()
![]()
La deuxième branche correspond à une fonction rationnelle, il faut donc trouver quel nombre annule le dénominateur puisque ce nombre sera le seul qui ne fera pas partie du domaine :
![]()
![]()
![]()
![]()
Ainsi, le domaine de la fonction par morceaux entière est l’union des deux sous-domaines :
![]()
![]()
Ou équivalent:
![]()
Comment représenter graphiquement une fonction par morceaux
Représenter une fonction par morceaux sur un graphique est simple, il suffit de représenter chaque intervalle séparément. Voyons comment représenter graphiquement une fonction par morceaux à l’aide d’un exemple :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \leq x<4 \\[2ex] 5 & \text{si} & x\geq 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8300142cc6b091ac5cad5378da5bde_l3.png)
Tout d’abord, il faut représenter la fonction de la première section, qui est une fonction affine . On fait donc un tableau de valeurs et, évidemment, pour cela on ne peut prendre que des valeurs de
![]() qui sont dans le premier intervalle :
qui sont dans le premier intervalle :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}-x+4} & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \le x<4 \\[2ex] 5 & \text{si} & x\ge 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cbef4257fa5fc2174760d825d8e126d_l3.png)
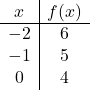
Maintenant, nous représentons les points sur le graphique et traçons la ligne :
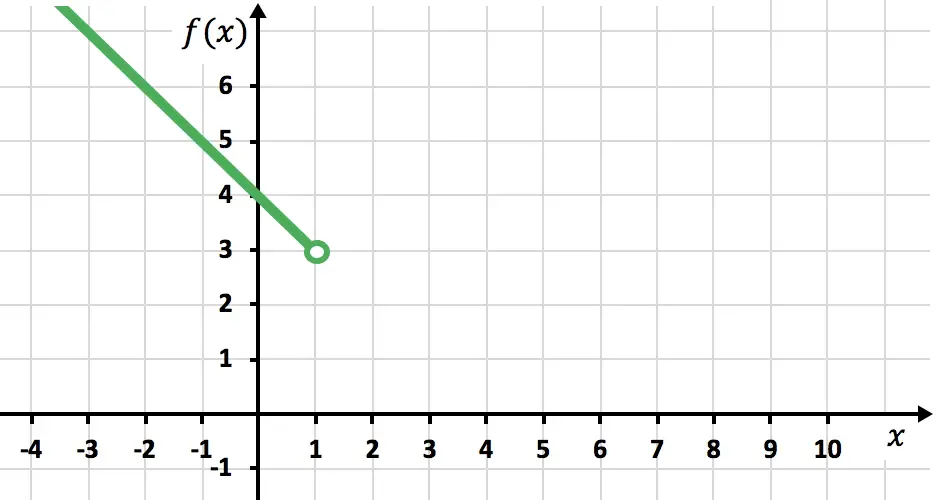
Dans cette section, le 1 n’est pas inclus, puisque le symbole
![]() de
de![]() signifie strictement inférieur à un. Il faut donc mettre un point ouvert dans
signifie strictement inférieur à un. Il faut donc mettre un point ouvert dans![]() pour indiquer qu’il n’est pas inclus.
pour indiquer qu’il n’est pas inclus.
Une fois que nous aurons représenté la première section, nous représenterons la deuxième section, qui va de
![]() (inclus) jusqu’à
(inclus) jusqu’à![]() (non inclus):
(non inclus):
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] \color{blue}\boxed{\color{black}x^2-4x+4} & \text{si} & 1 \leq x<4 \\[2ex] 5 & \text{si} & x\geq 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-262568a14e75d115e7b7466149e79db0_l3.png)
Il s’agit d’une fonction quadratique , on calcule donc d’abord le sommet de la parabole (en utilisant sa formule) puis on construit un tableau de valeurs autour du sommet :
![]()

Nous représentons les points obtenus sur la grille et dessinons la parabole :
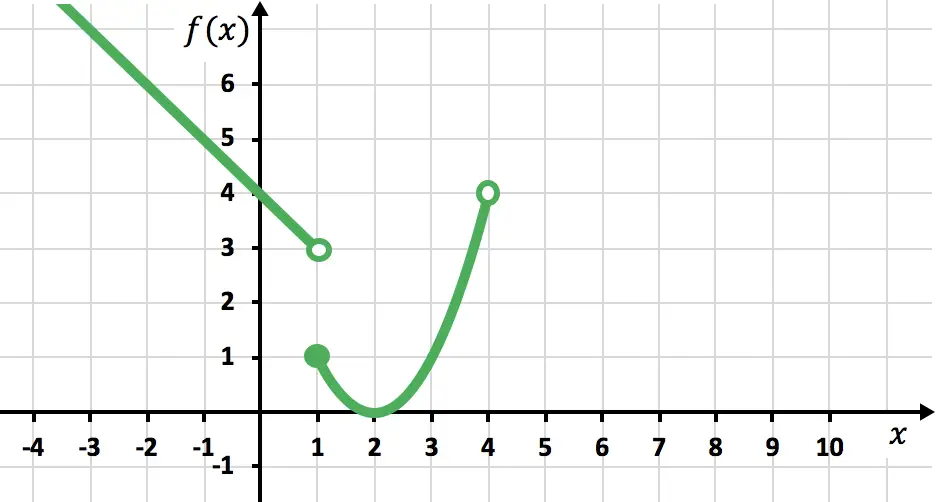
Notez que nous avons représenté la parabole avec un point fermé au début et un point ouvert à la fin. C’est parce que l’intervalle
![]() est d’abord défini par le signe
est d’abord défini par le signe![]() ce qui signifie que le 1 est inclus (car il a aussi le signe égal) et, par conséquent, il faut mettre un point fermé. Au lieu de cela, le signe
ce qui signifie que le 1 est inclus (car il a aussi le signe égal) et, par conséquent, il faut mettre un point fermé. Au lieu de cela, le signe![]() indique que 4 n’est pas inclus et c’est pourquoi un point ouvert doit être placé.
indique que 4 n’est pas inclus et c’est pourquoi un point ouvert doit être placé.
Et enfin nous représentons la dernière section :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \leq x<4 \\[2ex] \color{blue}\boxed{\color{black}5} & \text{si} & x\geq 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-2840124635e677a0c2269375d287631d_l3.png)
Dans cet intervalle, la fonction est constante et a toujours une valeur de 5. Par conséquent, nous traçons une ligne dans
![]() a partir de
a partir de![]() :
:
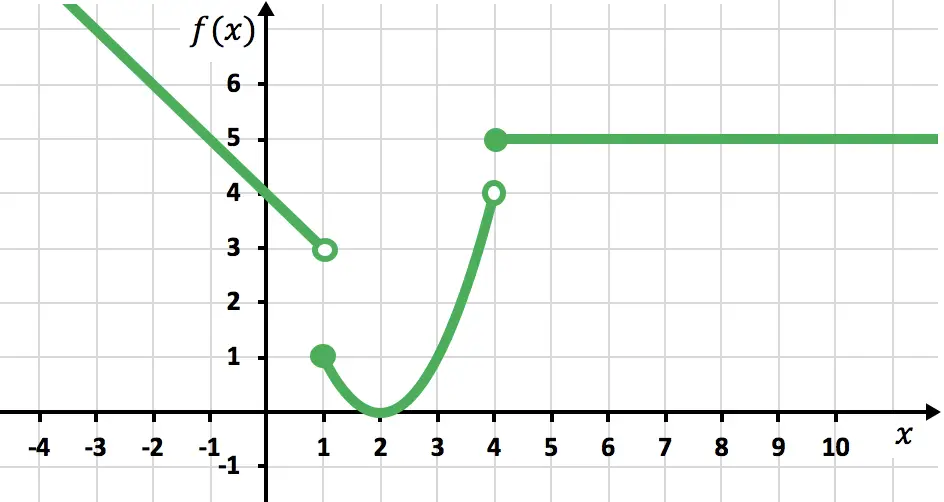
Contrairement à avant, dans cette section, il est inclus
![]() , parce que l’expression
, parce que l’expression![]() a le signe
a le signe![]() . Il faut donc le représenter par un point fermé pour indiquer que ce point est également inclus.
. Il faut donc le représenter par un point fermé pour indiquer que ce point est également inclus.
Et nous avons ainsi terminé la représentation graphique de la fonction définie en morceaux. Comme vous pouvez le constater, ce n’est pas très compliqué, il suffit de représenter chaque section séparément sur le même graphique.
Continuité d’une fonction par morceaux
Selon la notion de continuité, une fonction est continue en un point si les limites latérales existent en ce point et, en outre, sont égales à son image.
![]()
Ainsi, pour qu’une fonction définie en morceaux soit continue, la condition précédente doit être remplie en tous les points de chaque section et, en plus, aux points où la section change.
A titre d’exemple, nous allons analyser la continuité de la fonction suivante définie par intervalles :

La fonction est continue dans
![]() puisque la condition de continuité est remplie :
puisque la condition de continuité est remplie :
![]()
En fait, puisque la fonction est continue en ce point, les extrémités des deux intervalles ont été jointes.
Cependant, la fonction est discontinue dans
![]() car la condition de continuité n’est pas vérifiée :
car la condition de continuité n’est pas vérifiée :
![]()
En bref, la fonction définie par les morceaux est continue dans tous les nombres réels sauf dans
![]() où il y a une discontinuité.
où il y a une discontinuité.
Vous pouvez vous entraîner à faire plus d’exercices de ce type en cliquant sur le lien suivant :
➤ Voir : exercices résolus sur la continuité d’une fonction
Exercices résolus sur des fonctions définies par morceaux
Exercice 1
A partir de la fonction suivante définie par morceaux :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 1 & \text{si} & x<-3 \\[2ex] x+4 & \text{si} & -3 \leq x \leq 5 \\[2ex] 3x-6 & \text{si} & x>5 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3b7b7601d72637f68ea731ac6840d49_l3.png)
Calculer:
La fonction est toujours égale à 1 si
![]() est inférieur à -3. Pourtant:
est inférieur à -3. Pourtant:
![]()
En échange,
![]() C’est dans l’intervalle entre -3 et 5. Il faut donc faire le calcul avec la fonction de la deuxième section :
C’est dans l’intervalle entre -3 et 5. Il faut donc faire le calcul avec la fonction de la deuxième section :
![]()
Finalement,
![]() est supérieur à 5. Il faut donc faire le calcul avec la fonction de troisième section :
est supérieur à 5. Il faut donc faire le calcul avec la fonction de troisième section :
![]()
Exercice 2
A partir de la fonction suivante définie par morceaux :
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-5x-2 & \text{si} & x \leq -1 \\[2ex] 3x-7 & \text{si} & -1<x 2="" 4="" \leq="" \\[2ex]="" &="" \text{si}="" x="">4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a6e116ad73ccc70098b126b65d310cbd_l3.png)
Calculez les images suivantes :
En premier lieu,
![]() est inférieur à -1. Il faut donc faire le calcul avec la fonction de la première section :
est inférieur à -1. Il faut donc faire le calcul avec la fonction de la première section :
![]()
En échange,
![]() C’est dans l’intervalle entre -1 et 4. Il faut donc faire le calcul avec la fonction de deuxième section :
C’est dans l’intervalle entre -1 et 4. Il faut donc faire le calcul avec la fonction de deuxième section :
![]()
Finalement,
![]() sépare simplement le deuxième du troisième intervalle. Mais puisque le deuxième intervalle est
sépare simplement le deuxième du troisième intervalle. Mais puisque le deuxième intervalle est![]() f(4)=3\cdot 4-7 =12-7= \mathbf{5}
f(4)=3\cdot 4-7 =12-7= \mathbf{5} \displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right. 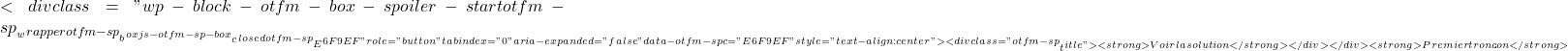 \displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}4} & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right. f(x)
\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}4} & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right. f(x)![]() x
x![]() f(x)= 4
f(x)= 4![]() x=-1 :
x=-1 : x=-1
x=-1![]() \displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] \color{blue}\boxed{\color{black}x+1} & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] \color{blue}\boxed{\color{black}x+1} & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right. 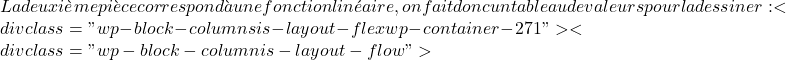 x=0 \longrightarrow f(0)=0+1=1x=1 \longrightarrow f(1)=1+1=2x=2 \longrightarrow f(2)=2+1=3
x=0 \longrightarrow f(0)=0+1=1x=1 \longrightarrow f(1)=1+1=2x=2 \longrightarrow f(2)=2+1=3![]() \begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}  \displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & x>4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & x>4 \end{array} \right. ![]() x
x![]() f(x)= 3
f(x)= 3 ![]() x=4 :
x=4 : x=4
x=4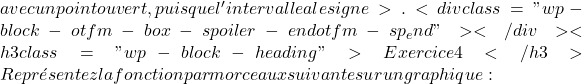 \displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right. 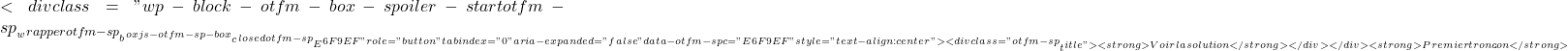 \displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black} x^2+2x+2 } & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black} x^2+2x+2 } & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right. ![]() x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot 1} = -1
x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot 1} = -1 ![]() f(x)
f(x) 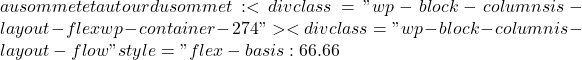 x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2(-1)+2 = 1 x= 0 \ \longrightarrow \ f(0)=0^2+2\cdot 0+2 =2 x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2(-2)+2 = 2 x= -3 \ \longrightarrow \ f(-3)=(-3)^2+2(-3)+2 = 5 x= 1 \ \longrightarrow \ f(1)=1^2+2\cdot 1+2 = 5
x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2(-1)+2 = 1 x= 0 \ \longrightarrow \ f(0)=0^2+2\cdot 0+2 =2 x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2(-2)+2 = 2 x= -3 \ \longrightarrow \ f(-3)=(-3)^2+2(-3)+2 = 5 x= 1 \ \longrightarrow \ f(1)=1^2+2\cdot 1+2 = 5 ![]() \begin{array}{c|c} x & f(x) \\ \hline -1 & 1 \\ 0 & 2 \\ -2 & 2 \\ 1 & 5 \\ -3 & 5 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline -1 & 1 \\ 0 & 2 \\ -2 & 2 \\ 1 & 5 \\ -3 & 5 \end{array} ![]() x\le1 :
x\le1 :  x=1
x=1![]() \displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] \color{blue}\boxed{\color{black}-x+8 }}}& \text{si} & x>1 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] \color{blue}\boxed{\color{black}-x+8 }}}& \text{si} & x>1 \end{array} \right. 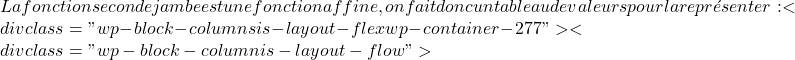 x= 1 \ \longrightarrow \ f(1)=-1+8=7x= 2 \ \longrightarrow \ f(2)=-2+8=6x= 3 \ \longrightarrow \ f(3)=-3+8=5
x= 1 \ \longrightarrow \ f(1)=-1+8=7x= 2 \ \longrightarrow \ f(2)=-2+8=6x= 3 \ \longrightarrow \ f(3)=-3+8=5![]() \begin{array}{c|c} x & f(x) \\ \hline 1 & 7 \\ 2 & 6 \\ 3 & 5 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 1 & 7 \\ 2 & 6 \\ 3 & 5 \end{array}![]() x>-1 :
x>-1 :  x=1
x=1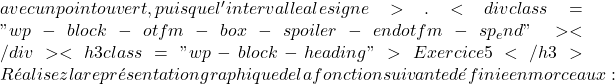 \displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right. 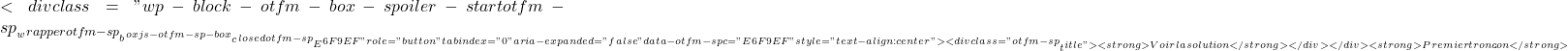 \displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}-x^2-4x+1}& \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}-x^2-4x+1}& \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right. ![]() x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot (-1)} = \cfrac{+4}{-2} = -2
x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot (-1)} = \cfrac{+4}{-2} = -2 ![]() f(x)
f(x) 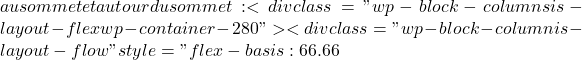 x= -2 \ \longrightarrow \ f(-2)=-(-2)^2-4(-2)+1 =5 x= -3 \ \longrightarrow \ f(-3)=-(-3)^2-4(-3)+1 =4 x= -4 \ \longrightarrow \ f(-4)=-(-4)^2-4(-4)+1 =1
x= -2 \ \longrightarrow \ f(-2)=-(-2)^2-4(-2)+1 =5 x= -3 \ \longrightarrow \ f(-3)=-(-3)^2-4(-3)+1 =4 x= -4 \ \longrightarrow \ f(-4)=-(-4)^2-4(-4)+1 =1 ![]() \begin{array}{c|c} x & f(x) \\ \hline -2 & 5 \\ -3 & 4 \\ -4 & 1 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline -2 & 5 \\ -3 & 4 \\ -4 & 1 \end{array} ![]() x<-2 :
x<-2 : x=-2
x=-2![]() \displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right. ![]() x
x![]() f(x)= 3
f(x)= 3 ![]() -2 \le x < 4 :
-2 \le x < 4 : x=-2
x=-2![]() x=-4
x=-4![]() \displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] \color{blue}\boxed{\color{black} 2x-10} & \text{si} & x \geq 4 \end{array} \right.
\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] \color{blue}\boxed{\color{black} 2x-10} & \text{si} & x \geq 4 \end{array} \right. 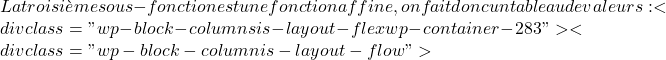 x=4 \longrightarrow f(4)=2\cdot 4-10=-2x=5 \longrightarrow f(5)=2\cdot 5-10=0x=6 \longrightarrow f(6)=2\cdot 6-10=2
x=4 \longrightarrow f(4)=2\cdot 4-10=-2x=5 \longrightarrow f(5)=2\cdot 5-10=0x=6 \longrightarrow f(6)=2\cdot 6-10=2 ![]() \begin{array}{c|c} x & f(x) \\ \hline 4 & -2 \\ 5 & 0 \\ 6 & 2 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 4 & -2 \\ 5 & 0 \\ 6 & 2 \end{array} ![]() x\ge 4 :
x\ge 4 :  x=4
x=4 \displaystyle f(x)= \left\{ \begin{array}{lcl} 2 & \text{si} & x\leq 0 \\[2ex] 5 & \text{si} & 0
\displaystyle f(x)= \left\{ \begin{array}{lcl} 2 & \text{si} & x\leq 0 \\[2ex] 5 & \text{si} & 0  f(x)=mx+n
f(x)=mx+n ![]() m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{-1-1}{1-0} = \cfrac{-2}{1} = -2
m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{-1-1}{1-0} = \cfrac{-2}{1} = -2 ![]() f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n
f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n 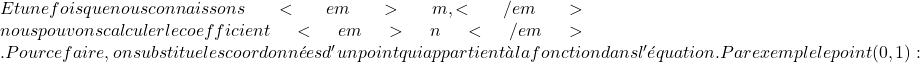 f(x)=-2x+n \ \xrightarrow{x \ = \ 0 \ ; \ f(x) \ = \ 1} \ 1=-2\cdot 0+n
f(x)=-2x+n \ \xrightarrow{x \ = \ 0 \ ; \ f(x) \ = \ 1} \ 1=-2\cdot 0+n ![]() 1=0+n 1=n
1=0+n 1=n ![]() \bm{f(x)=-2x+1}
\bm{f(x)=-2x+1}![]() x
x ![]() x<2
x<2![]() x=2
x=2![]() f(x)=mx+n
f(x)=mx+n ![]() m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{3-2}{4-3} = \cfrac{1}{1} = 1
m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{3-2}{4-3} = \cfrac{1}{1} = 1 ![]() f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n
f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n 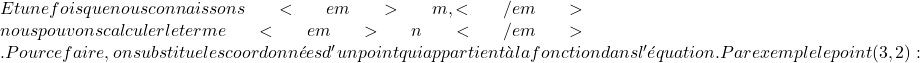 f(x)=x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 2} \ 2=3+n
f(x)=x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 2} \ 2=3+n ![]() 2-3=+n -1=n
2-3=+n -1=n ![]() \bm{f(x)=x-1}
\bm{f(x)=x-1}![]() x\ge 2
x\ge 2![]() x=2
x=2![]() \displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x<2 \\[2ex] x-1 & \text{si} & x\ge 2 \end{array} \right. $
\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x<2 \\[2ex] x-1 & \text{si} & x\ge 2 \end{array} \right. $