Fonction quadratique ou parabole

Cette page explique ce qu’est une fonction quadratique ainsi que toutes ses caractéristiques : courbure, sommet, points d’intersection avec les axes, etc. Vous découvrirez également comment représenter une fonction quadratique sur un graphique. Et enfin, vous pouvez vous entraîner avec des exemples, des exercices étape par étape et des problèmes sur les fonctions quadratiques.

Qu’est-ce qu’une fonction quadratique ?

La définition d’une fonction quadratique est la suivante :

En mathématiques, une fonction quadratique (ou parabolique) est une fonction polynomiale de degré 2, c’est-à-dire une fonction dans laquelle le terme du degré le plus élevé est du deuxième degré. Par conséquent, la formule d’une fonction quadratique est la suivante :

f(x)=ax^2+bx+c

Où:

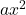  • ax^2 est le terme quadratique.
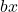  • bx est le terme linéaire.
  • c est le terme indépendant.

Le domaine d’une fonction quadratique est toujours constitué de nombres réels.

\text{Dom } f=\mathbff{R}

Concavité et convexité d’une fonction quadratique

Analyser la courbure d’une fonction quadratique ou parabolique est très simple, car elle ne dépend que du coefficient du deuxième degré.

  • Si le coefficienta est positif, la fonction quadratique est convexe (en forme\bm{\cup} ). Le sommet est donc un minimum.
  • Si le coefficienta est négatif, la fonction quadratique est concave (en forme de\bm{\cap} ). Le sommet est donc un maximum.
fonction quadratique ou parabole convexe
fonction quadratique ou parabole concave

Remarque : La communauté mathématique n’est toujours pas entièrement d’accord et, par conséquent, certains professeurs disent le contraire : ils appellent une fonction concave celle qui a la forme d’un

\bm{\cup} , et une fonction convexe qui a la forme de\bm{\cap} . Dans tous les cas, l’important est de savoir quelle forme a la fonction, quel que soit son nom.


Sommet d’une fonction quadratique

Pour représenter graphiquement une fonction quadratique, il est nécessaire de connaître les coordonnées du sommet de la parabole.

Pour trouver le sommet d’une fonction quadratique, nous devons calculer la coordonnée X du point en utilisant la formule suivante :

\displaystyle x=\frac{-b}{2a}

Ensuite, nous pouvons trouver l’autre coordonnée du sommet en calculant l’image de la fonction en ce point :

\displaystyle f\left(\frac{-b}{2a}\right)

Ainsi les coordonnées du sommet d’une fonction quadratique (ou parabole) sont :

\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)

Points de coupe avec les axes d’une fonction quadratique

Une parabole coupe toujours l’axe des ordonnées (axe Y), et cela se produit lorsque

x=0. Par conséquent, pour calculer le point de coupure d’une fonction quadratique avec l’axe Y, il faut résoudref(0).

Par exemple, le point d’intersection avec l’axe OY de la fonction quadratique suivante est :

f(x)=x^2-2x+1

f(0)=0^2-2\cdot 0+1 = 1

\bm{(0,1)}

D’autre part, le point de coupure d’une fonction quadratique avec l’axe des abscisses (axe X) se produit lorsque

f(x)=0. Donc pour calculer le point d’intersection avec l’axe X il faut résoudre l’équationf(x)=0.

A titre d’exemple, vous avez ci-dessous le calcul du point de coupure avec l’axe OX de la même fonction quadratique :

f(x)=x^2-2x+1

0=x^2-2x+1

On résout l’équation quadratique avec la formule générale :

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1

Le point d’intersection de la fonction quadratique avec l’axe X est donc :

\bm{(1,0)}

Dans ce cas, nous avons obtenu une seule solution de l’équation quadratique, mais nous aurions pu obtenir deux solutions. Dans ce cas, cela signifie que la fonction quadratique coupe l’axe X en deux points différents.

Exemple de représentation d’une fonction quadratique ou parabolique


Voyons comment représenter une fonction quadratique sur un graphique à l’aide d’un exemple.

  • Représentez graphiquement la fonction suivante :

f(x)=x^2-4x+5

La première chose à faire est de calculer le sommet de la parabole. Pour ce faire, nous utilisons la formule que nous avons vue ci-dessus :

x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2

Une fois que nous savons où sera le sommet, nous devons construire une table de valeurs :   On calcule la valeur de la fonction au sommet et aux points qui l’entourent :

f(x)=x^2-4x+5

  • x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1
  • x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2
  • x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2
  • x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5
  • x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5

\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}

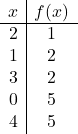
Vous pouvez également calculer les points de coupure de la fonction quadratique avec les axes cartésiens pour mieux dessiner la parabole, mais ce n’est pas strictement nécessaire.

Nous représentons maintenant les points obtenus sur un graphique :

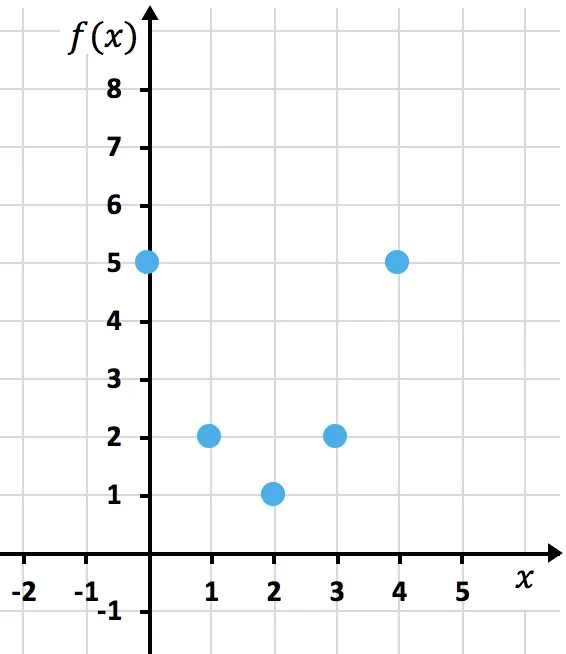
exemple de la façon de représenter une fonction quadratique ou parabolique

Et enfin, on rejoint les points formant la parabole. Puis on allonge les branches de la parabole pour indiquer qu’elle continue vers le haut :

représentation d'une fonction quadratique ou parabolique

Exercices résolus sur les fonctions quadratiques

Exercice 1

Trouvez le sommet de la fonction quadratique suivante :

f(x)=2x^2+8x+4

Nous calculons d’abord la coordonnée X du sommet en utilisant la formule :

x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2

Et maintenant nous calculons l’autre coordonnée en évaluant la fonction au point :

\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}

Le sommet de la fonction quadratique est donc :

\bm{(-2,-4)}

Exercice 2


Trouvez les points de coupure de la fonction suivante avec les axes :

f(x)=x^2-4x+3

Pour calculer le point de coupure avec l’axe Y, nous devons calculer

f(0):

f(0)=0^2-4\cdot 0+3 = 3

La fonction passe donc par l’axe Y au point :

\bm{(0,3)}

Et pour trouver les points de coupure avec l’axe X, nous devons résoudre

f(x)=0:

f(x)=x^2-4x+3

0=x^2-4x+3

On calcule les racines de l’équation du deuxième degré avec la formule :

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}

La fonction coupe donc l’axe X en deux points :

\bm{(1,0) \qquad (3,0)}

Exercice 3

Représentez graphiquement la fonction quadratique suivante :

f(x)=-x^2+4x+1

Il s’agit d’une fonction quadratique. Par conséquent, pour la représenter il faut d’abord calculer l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2

Maintenant, nous créons la table de valeurs. Pour ce faire, nous calculons la valeur de

f(x) au sommet et autour du sommet :

x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5

x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4

x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4

x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1

x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1

\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}

Et enfin, nous représentons les points sur le graphique et dessinons la parabole :

exemple de fonction quadratique

Exercice 4

Faites la représentation graphique de la fonction quadratique suivante :

f(x)=-2x^2-8x-1

Il s’agit d’une fonction du second ordre. Par conséquent, pour la représenter il faut d’abord trouver l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2

Maintenant, nous construisons le tableau des valeurs. Pour ce faire, nous calculons la valeur de

f(x) au sommet et autour du sommet :

x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7

x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5

x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5

x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1

x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1

\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}

Enfin, nous représentons les points sur le graphique et dessinons la parabole :

exercice résolu étape par étape de la fonction quadratique

Exercice 5

Représentez la fonction quadratique incomplète suivante sur un graphique :

f(x)=x^2+2

C’est une fonction polynomiale de degré deux. Par conséquent, pour la représenter il faut d’abord calculer l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0

Dans ce cas, la fonction est incomplète, puisqu’elle n’a pas de terme du premier degré. Pour cela

b=0 .

Maintenant, nous faisons le tableau des valeurs. Pour ce faire, nous calculons la valeur de

f(x) au sommet et autour du sommet :

x= 0 \ \longrightarrow \ f(0)=0^2+2=2

x= 1 \ \longrightarrow \ f(1)=1^2+2=3

x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3

x= 2 \ \longrightarrow \ f(2)=2^2+2=6

x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6

\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}

Enfin, nous traçons les points sur le graphique et dessinons la parabole :

exercices résolus pour représenter une fonction quadratique incomplète

Exercice 6

Résolvez le problème suivant lié aux fonctions quadratiques :

Le coût de production d’un produit est défini par la fonction suivante :

f(x)=x^2-12x+76

Où

x sont les unités produites (en milliers) etf(x) est le coût de production des unités (en milliers d’euros).

  • Représente la fonction de coût de production sur un graphique.
  • Détermine combien de milliers d’unités doivent être produites pour minimiser les coûts.

Il s’agit d’une fonction quadratique. Par conséquent, pour la représenter il faut d’abord trouver l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6

Maintenant, nous faisons le tableau des valeurs. Pour ce faire, nous calculons la valeur de

f(x) au sommet et autour du sommet :

x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40

x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41

x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41

x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44

x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44

\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}

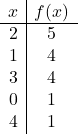
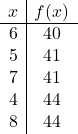
Maintenant, nous représentons les points sur le graphique et dessinons la parabole :

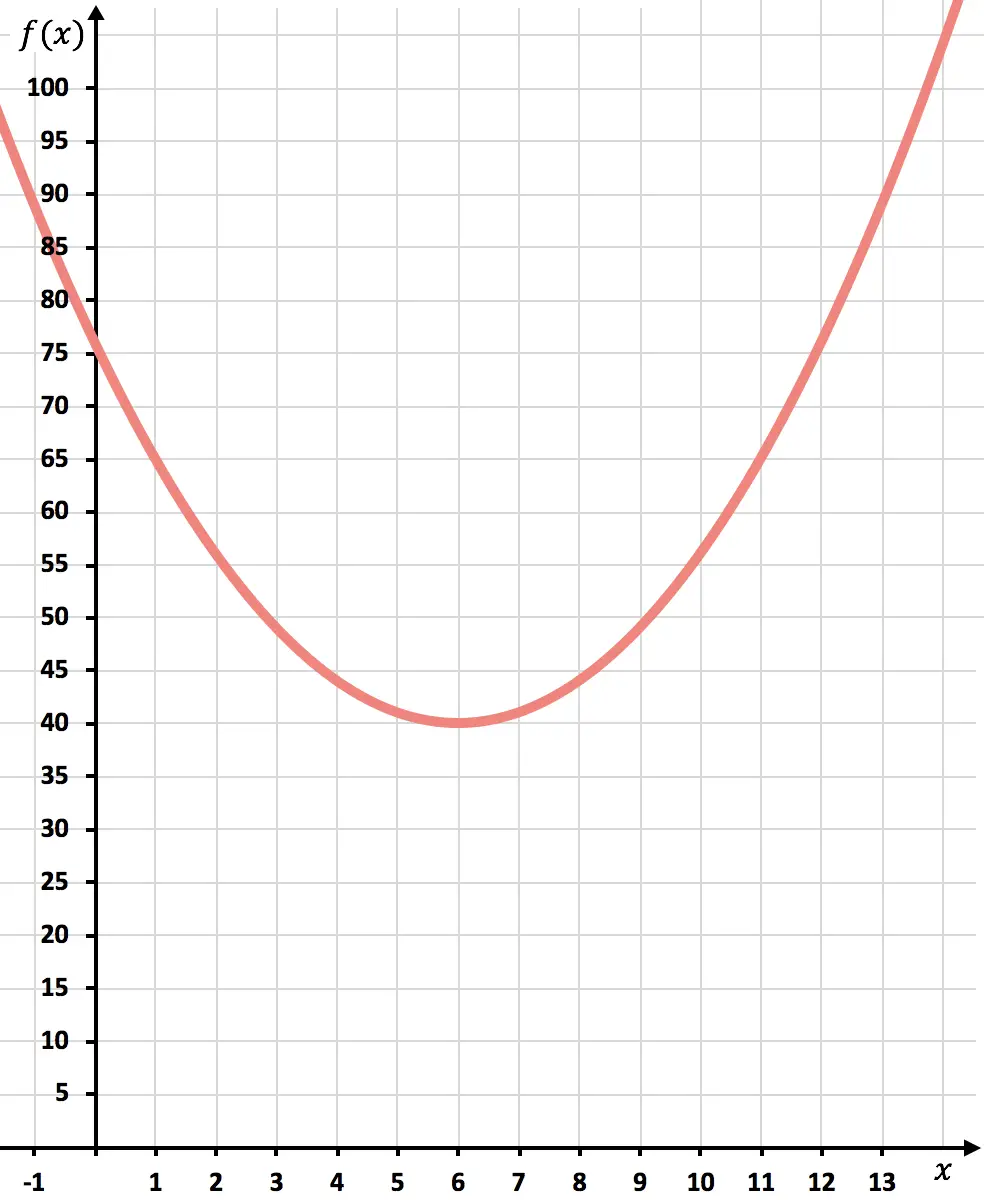
problème de fonction quadratique ou parabolique

Une fois la fonction représentée, nous verrons à quel point les coûts sont minimisés.

Comme le montre le graphique, les coûts minimaux seront atteints au sommet de la parabole. Parce que c’est là que la fonction prend la plus petite valeur.

En conclusion, les coûts seront minimisés en produisant 6 000 unités.

Exercice 7

Résolvez le problème de fonction quadratique suivant :

Un athlète effectue un lancer de javelot dont la trajectoire peut être représentée par la fonction suivante :

h(x) = -0,025x^2+2x+2

Où

x sont les mètres parcourus par le javelot eth sa hauteur (également en mètres).

Quelle est la hauteur maximale que peut atteindre le javelot ?

C’est une fonction quadratique, donc la trajectoire du javelot sera une parabole.

De plus, comme le coefficient du terme quadratique est négatif (-0,025), la parabole aura une forme de U inversé et ses branches iront vers le bas. Ainsi le javelot atteindra la hauteur maximale au sommet, puisque ce sera le point le plus haut de la parabole.

On calcule donc l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40

Et puis nous calculons la hauteur à laquelle se trouvera le javelot à ce point en évaluant la fonction dans

x=40:

h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42

La hauteur maximale que peut atteindre le javelot est donc de 42 mètres.

Exercice 8

Résolvez le problème suivant concernant les fonctions quadratiques :

Les coûts de production (en euros) d’une entreprise sont définis par la fonction suivante :

C(q)=40000+20q+q^2

Où

q sont les unités produites.

Et le prix de vente de chaque unité est de 520 €.

  • Quel bénéfice l’entreprise réalisera-t-elle si elle vend 150 unités ?
  • Combien d’unités doivent être vendues pour un profit maximum ?

L’entreprise gagne 520 € pour chaque unité vendue. Par conséquent, la fonction qui définit le revenu est :

I(q)=520\cdot q = 520q

Où

q sont les unités vendues.

Mais ils nous interrogent sur le profit, c’est-à-dire le revenu moins les coûts. Nous soustrayons donc les revenus moins les coûts pour obtenir la fonction qui décrit le bénéfice de l’entreprise :

B(q)=I(q)-C(q)

B(q)=520q - (40000+20q+q^2)

B(q)=520q - 40000-20q-q^2

B(q)=-q^2 + 500q - 40000

Une fois que l’on connaît la fonction qui décrit le profit de l’entreprise, il suffit de substituer 150 dans l’expression de la fonction pour calculer le profit que l’entreprise obtiendra en vendant 150 unités :

\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}

Ainsi, en vendant 150 unités, l’entreprise réalisera un bénéfice de 12 500 €.

La déclaration nous demande également de calculer combien d’unités le profit maximum est atteint.

La fonction qui décrit le profit est une fonction quadratique, elle aura donc la forme d’une parabole. Et comme le coefficient du terme du deuxième degré est négatif (-1), la parabole aura une forme de U inversé et ses branches iront vers le bas. Par conséquent, les gains maximaux seront réalisés au sommet, puisqu’il s’agit du point culminant de la parabole.

On calcule donc l’abscisse du sommet de la parabole avec la formule :

x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250

L’entreprise réalisera donc le maximum de profit en vendant 250 unités.

En revanche, même si le communiqué ne le demande pas, on peut déterminer le profit qui sera réalisé en vendant ces 250 unités :

B(250) =-(250)^2 + 500\cdot250- 40000= 22500 €


Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top