▷ Comment savoir si une fonction est continue (exercices résolus)

Dans cet article, nous expliquons ce que sont les fonctions continues et comment déterminer si une fonction est continue en un point ou non. De plus, vous trouverez les propriétés des fonctions continues et l’analyse de la continuité des fonctions les plus courantes. Enfin, vous pouvez vous entraîner avec des exercices résolus sur la fonction continue pour bien comprendre le concept.

Qu’est-ce qu’une fonction continue ?

La continuité d’une fonction peut être étudiée graphiquement. Une fonction continue est une fonction qui peut être représentée sur un graphique sans retirer le crayon du papier.

Fonction continue

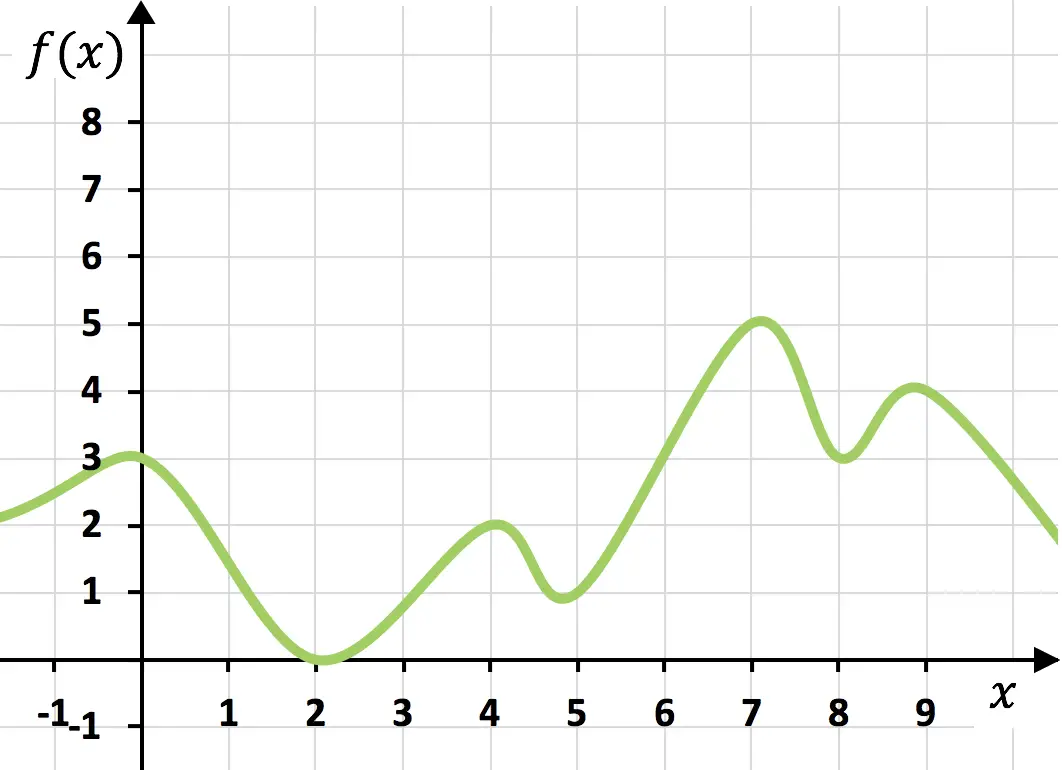
La fonction ci-dessus est continue car elle peut être dessinée d’un seul coup sans lever la main du papier.

En revanche, lorsque la condition de continuité précédente n’est pas remplie dans une fonction, on dit qu’il s’agit d’une fonction discontinue .

Fonction discontinue

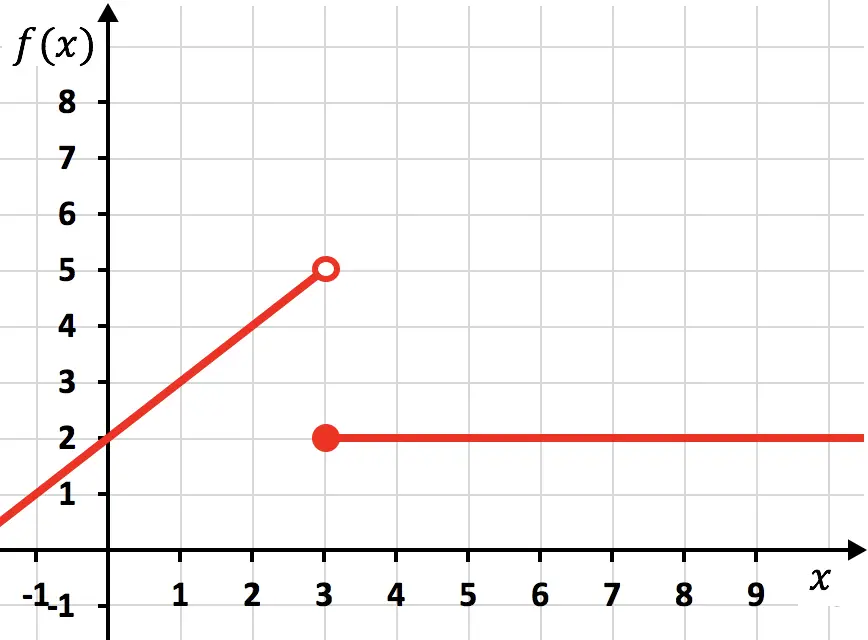
La fonction précédente est discontinue car pour la représenter il faut faire deux traits avec le crayon. Dans ce cas, la fonction cesse d’être continue à x=3, on dit donc que x=3 est un point de discontinuité .

De plus, il existe trois types de discontinuités : la discontinuité évitable, la discontinuité inévitable à saut fini et la discontinuité inévitable à saut infini. Dans le lien suivant, vous pouvez voir à quoi ressemble chaque type de discontinuité et ce qui est différent de chacun d’eux :

➤ Voir : types de discontinuités

Continuité d’une fonction en un point

Une fois que nous aurons vu à quoi ressemble le graphique d’une fonction continue, nous allons voir comment savoir si une fonction est continue ou non analytiquement.

Mathématiquement, une fonction est continue en un point si les trois conditions suivantes sont remplies :

La fonction existe en ce point, c’est-à-dire que l’image du point existe.

$\exists \ f(a)$

Il y a la limite de la fonction à ce stade. Par conséquent, les limites latérales gauche et droite de la fonction en ce point sont égales.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

L’image du point coïncide avec la limite de la fonction en ce point.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Ainsi, si les trois conditions de continuité sont remplies en tous points d’une fonction, la fonction est continue.

A titre d’exemple, nous allons analyser la continuité de la fonction par morceaux suivante :

continuité d'une fonction définie par morceaux

Même si vous changez de section, au point

$x=-2$ La fonction est continue, puisque les limites latérales de la fonction en ce point sont égales et coïncident en outre avec la valeur de la fonction en ce point.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

En revanche, la fonction n’est pas continue au point

$x=4$ car les deux limites latérales sont différentes et, par conséquent, la limite de la fonction n’existe pas à ce point :

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

En bref, la fonction définie par les morceaux est continue dans tous les nombres réels sauf dans

$x=4,$ où il y a une discontinuité.

On peut également vérifier que la fonction est discontinue dans

$x=4$ car pour le représenter graphiquement, il est nécessaire de retirer le crayon du papier à ce stade.

Continuité des fonctions élémentaires

Certains types de fonctions sont continues de par leurs caractéristiques :

Les fonctions constantes sont continues dans tous les nombres réels.

$f(x)=k$

Les fonctions polynomiales sont continues pour tous les nombres réels.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Les fonctions rationnelles (ou fractionnaires) sont continues dans tous les nombres réels sauf dans les valeurs qui annulent le dénominateur de la fraction, en ces points la fonction présente une discontinuité.

$f(x)=\cfrac{p(x)}{q(x)}$

Les fonctions exponentielles sont continues sur l’ensemble des nombres réels :

$f(x)=a^x$

Les fonctions logarithmiques sont continues en tous les points qui rendent leur argument positif.

$f(x)=\log_a (x)$

La continuité des fonctions irrationnelles , ou fonctions avec racines, dépend de l’indice du radical (n). Si l’index est pair, ce sont des fonctions continues en tous points qui rendent l’argument racine égal ou supérieur à zéro. Mais si l’indice est impair, ce sont des fonctions continues sur tous les nombres réels.

$f(x)=\sqrt[n]{x}$

La continuité des fonctions trigonométriques dépend du type de fonction. La fonction sinus et la fonction cosinus sont continues sur l’ensemble des nombres réels, mais la fonction tangente est discontinue aux points 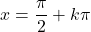$\displaystyle x=\frac{\pi}{2}+k\pi$ (où k est un entier).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Propriétés des fonctions continues

Sean

$f(x)$ et $g(x)$ deux fonctions continues au point $x=a,$ ensuite:

La somme de deux fonctions continues en un point est une autre fonction continue en ce point.

$f(x)+g(x)$

Le produit de deux fonctions continues en un point est égal à une autre fonction continue en ce point.

$f(x)\cdot g(x)$

La division de deux fonctions continues en un point entraîne une autre fonction continue en ce point, tant que ce point n’annule pas la fonction de division.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

La composition de deux fonctions continues en un point donne naissance à une fonction continue en ce même point.

$f(x)\circ g(x)$

➤ Voir : qu’est-ce qu’une fonction composite ?

Exercices résolus sur la continuité d’une fonction

Exercice 1

Trouvez les discontinuités de la fonction représentée dans le graphique suivant. Déterminez également de quel type de discontinuité il s’agit.

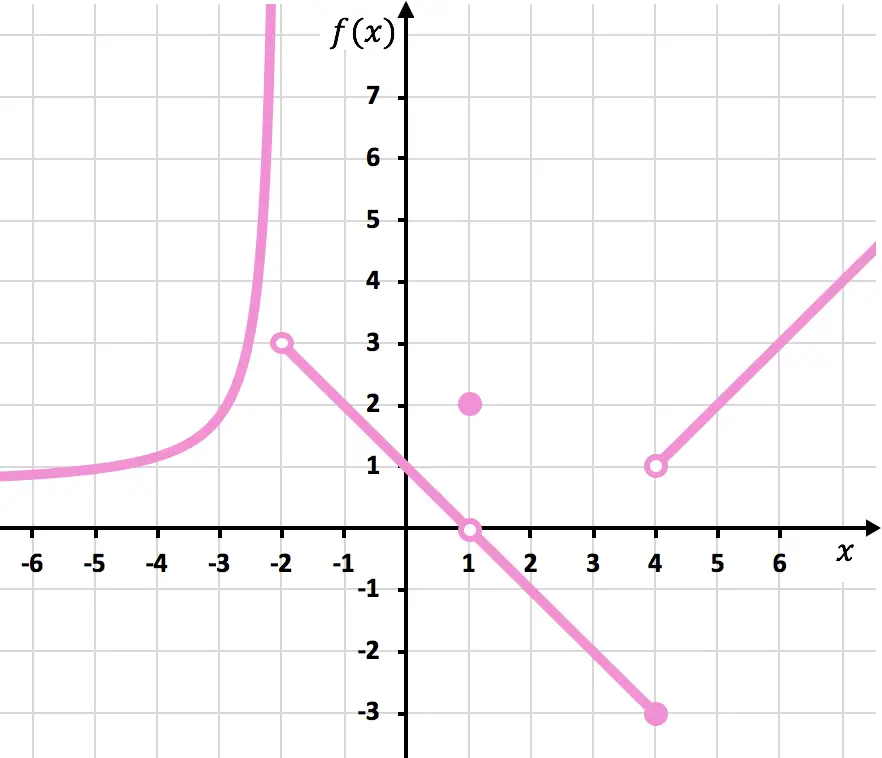
exercice résolu les discontinuités des fonctions

Remarque : pour réaliser cet exercice nous vous recommandons de voir dans un premier temps quels sont les différents types de discontinuités et comment elles sont identifiées. Vous pouvez voir l’explication dans le lien du principe des types de discontinuités .

Voir la solution

Pour dessiner la fonction il faut lever le crayon en x=-2, en x=1 et en x=4. La fonction est donc discontinue en ces trois points.

À x=-2, la limite latérale à gauche est +∞ et la limite latérale à droite est 3. Ainsi, puisque l’une des limites latérales est infinie, la fonction a une inévitable discontinuité de saut infini à x=- 2 .

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

La limite de la fonction en x=1 est 0 et, par contre, la valeur de la fonction en x=1 est égale à 2. La fonction présente donc une discontinuité évitable en x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

À x = 4, la limite latérale à gauche est -3 et la limite latérale à droite est 1. Par conséquent, puisque les deux limites latérales sont différentes et qu’aucune d’elles ne donne l’infini, la fonction a inévitablement une discontinuité de saut fini en x =4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Exercice 2

Déterminez les points auxquels la fonction représentée dans le graphique suivant est discontinue.

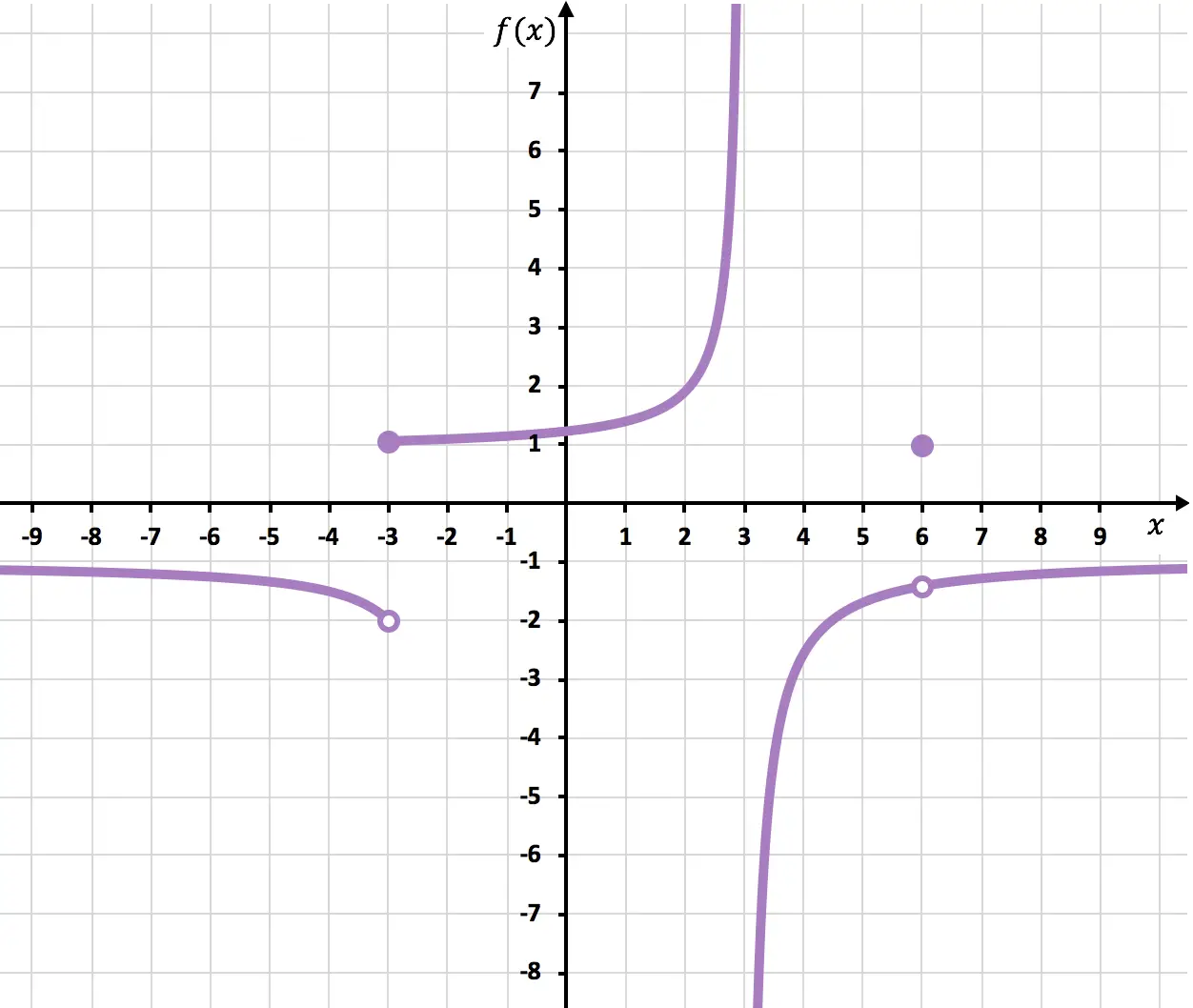
exercice résolu sur les types de discontinuités d'une fonction

Voir la solution

Au point x=6 la fonction est interrompue car il y a un point ouvert. La limite lorsque x s’approche de 6 est -1,4 mais f(6)=1. La fonction a donc une discontinuité évitable en x=6 car la valeur de la limite ne coïncide pas avec la valeur de la fonction :

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

A x=-3 les limites latérales ne coïncident pas et aucune ne donne l’infini. La fonction a donc une inévitable discontinuité de saut fini à x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

Et enfin, la fonction a une inévitable discontinuité de saut infinie en x = 3, puisqu’au moins une limite latérale à ce point aboutit à l’infini.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Exercice 3

Analyser la continuité de la fonction rationnelle suivante :

$\displaystyle f(x)= \frac{2}{x-5}$

Voir la solution

Les fonctions rationnelles sont continues dans tout leur domaine, c’est-à-dire dans tous les nombres réels à l’exception des valeurs qui annulent le dénominateur. Par conséquent, nous fixons le dénominateur de la fonction rationnelle égal à zéro pour voir quels points n’appartiennent pas au domaine :

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

La fonction sera donc continue en tous points sauf x=5.

Exercice 4

Analysez la continuité de la fonction par morceaux suivante :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Voir la solution

La fonction est continue aussi bien dans la première section,

$5x-2$ , comme dans la deuxième section, $x^2+2$ , puisqu’il s’agit de fonctions polynomiales.

Ainsi, le seul point auquel la fonction pourrait être discontinue est le point de rupture de la fonction par morceaux. Calculons donc les limites latérales à ce stade :

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

Les deux limites latérales coïncident donc, la limite de la fonction lorsque x tend vers 1 est égale à 3 :

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

De plus, l’image de x=1 est également 3 :

$f(1)=1^2+2=\bm{3}$

Ainsi, puisque la limite de la fonction en x=1 est égale à l’image dudit point, la fonction est continue au point x=1. Et par conséquent, il est continu dans tous les nombres réels.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Exercice 5

Étudiez la continuité de la fonction irrationnelle suivante :

$f(x)=\sqrt{2x+6}$

Voir la solution

C’est une fonction radicale d’indice pair, donc la fonction sera continue tant que l’argument du radical est supérieur à 0 (car la racine carrée d’un nombre négatif n’existe pas) :

$2x+6\ge 0$

On résout l’inégalité :

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

La solution est constituée de tous les nombres supérieurs ou égaux à -3. La fonction est donc continue sur l’intervalle de son domaine :

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Exercice 6

Analysez la continuité de la fonction logarithmique suivante :

$f(x)=\log_3 (-3x+6)$

Voir la solution

Il s’agit d’une fonction logarithmique, et il n’existe ni le logarithme d’un nombre négatif ni le logarithme de 0. Par conséquent, la fonction existera tant que l’argument du logarithme est positif (supérieur à zéro) :

$-3x+6>0$

On résout l’inégalité :

$-3x>-6$

$x<\cfrac{-6}{-3}$

N’oubliez pas que lorsque vous divisez un nombre négatif par l’autre côté d’une inégalité, vous devez inverser le signe de l’inégalité.

$x<2$

La solution est constituée de tous les nombres inférieurs à 2. Le domaine de définition de la fonction est donc :

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

La fonction est donc continue en tout point de son domaine.

Exercice 7

Calculez la continuité de la fonction suivante :

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Voir la solution

Au dénominateur de la fraction, nous avons un radical avec un indice pair, donc la fonction existera chaque fois que le contenu de la racine est égal ou supérieur à zéro :

$-2x-8\geq 0$

Mais aussi, la racine est au dénominateur de la fraction, et le dénominateur d’une fraction ne peut jamais être 0. Donc la fonction n’existera que si le contenu de la racine est strictement supérieur à 0 :

$-2x-8> 0$

Maintenant, nous résolvons l’inégalité :

$-2x>8$

$x<\cfrac{8}{-2}$

N’oubliez pas que lorsque nous changeons les côtés d’un nombre négatif en multipliant ou en divisant une inégalité, nous devons également faire pivoter le signe de l’inégalité.

$x<-4$

Le résultat est tous les nombres inférieurs à -4. Ainsi le domaine de la fonction, et donc sa continuité, sont définis par l’intervalle suivant :

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Exercice 8

Calculer la valeur de k pour que la fonction soit continue tout au long

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.$

Voir la solution

Pour que la fonction soit continue, il faut que les deux limites latérales au point de rupture donnent le même résultat. On calcule donc d’abord la limite latérale au point de rupture de la pièce qui n’a pas k :

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Par conséquent, pour que la fonction par morceaux soit continue, l’autre limite latérale doit également être égale à 7.

On essaie de calculer l’autre limite latérale :

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Ainsi, pour que la fonction soit continue, il faut que les deux limites latérales d’un point quelconque donnent le même résultat. Nous fixons donc l’expression obtenue à partir de la limite égale à 7 (le résultat de l’autre limite latérale).

$2k -1= 7$