▷ Composition de fonctions (ou fonction composite)

Dans cet article, nous expliquons ce qu’est la fonction composite (ou composition de fonctions). De plus, vous pourrez voir plusieurs exemples de fonctions composites et comment le domaine de ce type de fonctions est calculé. Enfin, vous trouverez les propriétés de la composition des fonctions et plusieurs exercices pas à pas pour vous entraîner.

Qu’est-ce que la composition des fonctions ?

La composition de fonctions consiste à évaluer successivement la même valeur de la variable indépendante (x) dans deux ou plusieurs fonctions . Par exemple, la composition des fonctions (gof)(x) donne la fonction composite g[f(x)].

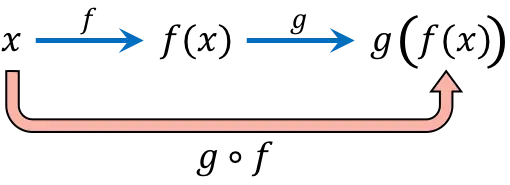
L’expression de la fonction composite

$g\circ f$ on lit « f composé avec g » ou « f suivi de g ».

Notez que l’ordre est important dans la composition des fonctions, la fonction qui se trouve à droite du symbole de composition est appliquée en premier

$(f)$ puis la fonction à gauche du symbole de composition $(g).$

Exemple de composition de fonctions

Étant donné la définition d’une fonction composite, voyons un exemple de la façon de calculer la composition de deux fonctions.

Étant donné les deux fonctions différentes suivantes :

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Calculer la fonction composée

$\left(g \circ f\right)(x)$ et l’évaluer dans $x=3.$

La composition des fonctions

$\left(g \circ f\right)(x)$ Cela signifie que nous devons réaliser la fonction composite suivante :

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Pour le résoudre, nous remplaçons

$f(x)$ par son expression algébrique :

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

Et maintenant nous prenons la fonction de

$g(x)=\cfrac{x+4}{2}$ et on met l’expression $3x+1$ où il y en a un $x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

De cette manière nous avons déjà calculé la fonction f composée de g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Enfin, pour évaluer la fonction composite dans

$x=3$ Il suffit de calculer l’image de la fonction dans ladite valeur :

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Domaine de fonctions composites

Normalement, lorsque nous effectuons des opérations sur des fonctions, le domaine de la fonction résultante est l’intersection des domaines des fonctions d’origine. Cependant, cette propriété n’est pas satisfaite par la composition des fonctions.

Le domaine de la composition des fonctions

$(g\circ f)(x)$ est équivalent à l’ensemble de toutes les valeurs de x dans le domaine de la fonction $f$ tel que $f(x)$ appartient au domaine de la fonction $g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Par conséquent, pour calculer le domaine de définition d’une fonction composite, vous devez d’abord trouver le domaine de chaque fonction séparément, puis le domaine de la fonction résultant de l’opération. Ainsi, le domaine de composition des fonctions sera constitué de toutes les valeurs qui satisfont à la condition mathématique précédente.

👉 N’oubliez pas que si vous rencontrez un problème que vous ne savez pas comment résoudre, vous pouvez nous le demander dans les commentaires ci-dessous !

Propriétés de la composition des fonctions

Les fonctions composites ont les caractéristiques suivantes :

La composition des fonctions a la propriété associative, par conséquent, l’équation suivante est toujours vraie :

$f\circ (g\circ h)=(f\circ g)\circ h$

En général, la composition des fonctions n’est pas commutative, donc l’ordre de l’opération détermine le résultat :

$f\circ g\neq g\circ f$

L’élément neutre de la composition des fonctions correspond à la fonction identité 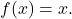$f(x)=x.$ Ainsi, toute fonction composée avec la fonction d’identité aboutit à la fonction elle-même :

$f\circ id = id \circ f = f$

$id = x$

Calculer l’inverse de la composition de deux fonctions équivaut à trouver d’abord l’inverse de chaque fonction puis à déterminer la fonction composée :

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

La fonction inverse agit également comme un élément symétrique de la fonction composée, puisque la composition d’une fonction avec son inverse équivaut à la fonction identité :

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

La dérivée de la composition de deux fonctions est calculée à l’aide de la règle de la chaîne :

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Voir : quelle est la règle de la chaîne ?

Exercices résolus sur la composition des fonctions

Exercice 1

Étant donné les deux fonctions suivantes :

$f(x)=x-2 \qquad g(x)= 5x + 4$

Calculer les compositions des fonctions f composées avec g et g composées avec f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Voir la solution

La composition des fonctions

$\left(g \circ f\right)(x)$ signifie calculer la fonction composée suivante :

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Donc, pour le résoudre, nous remplaçons

$f(x)$ pour son expression : $f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$ Cela signifie que dans l’expression de $g(x) =5x+4$ il faut remplacer la variable $x$ pour $x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Pourtant:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Par contre, pour trouver la fonction g composée de f il faut faire la même procédure mais avec l’ordre inversé :

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Cet exercice démontre également la propriété selon laquelle les fonctions composites ne sont pas commutatives, puisque le résultat dépend de l’ordre dans lequel les fonctions sont appliquées.

Exercice 2

Étant donné les deux fonctions suivantes :

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Calcule la composition des fonctions f composées avec g .

$(g\circ f)(x)$

Voir la solution

La fonction f composée de g signifie résoudre la fonction composée suivante :

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

On remplace donc la fonction f(x) par son expression :

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

Et maintenant nous devons remplacer

$x$ pour $x^2-3$ dans l’expression de la fonction g(x) :

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

En bref, le résultat de la composition des fonctions est :

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Exercice 3

Étant donné les deux fonctions quadratiques suivantes :

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Déterminez le résultat de la composition de fonctions suivante :

$(g\circ f)(2)$

Voir la solution

$\left(g \circ f\right)(2)$ consiste à trouver la fonction composite suivante :

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Donc, pour résoudre la fonction composite, nous calculons d’abord

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Par conséquent, comme

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Donc pour trouver la valeur de la fonction composée il suffit de calculer

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

En résumé, le résultat du problème de composition des fonctions est :

$\bm{\left(g \circ f\right)(2) =8}$

Exercice 4

Étant donné les deux fonctions suivantes :

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Trouvez le résultat de g composé avec f en x=2 :

$(f\circ g)(2)$

Voir la solution

Dans ce cas, il faut calculer la fonction composée suivante :

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Alors d’abord nous trouvons

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

Et donc, comme

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Donc pour résoudre la fonction composite, nous devons calculer

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$

En conclusion, le résultat de l’exercice des fonctions composées est :

$\bm{\left(f \circ g\right)(2)=1}$

Exercice 5

Étant donné les trois fonctions suivantes :

$f(x) = x+1 \qquad g(x)= 3x - 5\qquad h(x) = \sqrt{x} - 3$

Calculez la composition suivante des 3 fonctions :

$(h \circ g \circ f )(x)$

Voir la solution

L’expression

$\left(h \circ g \circ f\right)(x)$ Cela signifie qu’il faut calculer la fonction composée suivante :

$\left(h \circ g \circ f\right)(x) = h \bigg( g\Big(f(x)\Big) \bigg)$

Alors d’abord, nous déterminons

$g\Big( f(x)\Big):$

$\begin{aligned}g\Big( f(x)\Big)&=g\Big(x+1 \Big)\\[2ex]&= 3(x+1)-5\\[2ex]&= 3x+3-5\\[2ex]&= 3x-2\end{aligned}$

Et maintenant nous calculons

$h \bigg( g\Big(f(x)\Big) \bigg)$ . Pour ce faire, on remplace l’expression trouvée à partir de $g\Big(f(x)\Big)$ où un apparaît $x$ dans la fonction $h(x):$