Vous découvrirez ici ce qu’est la règle de chaîne et comment dériver des fonctions à l’aide de la règle de chaîne. De plus, vous pourrez voir plusieurs exemples de dérivées résolues avec la règle de la chaîne et vous pourrez même vous entraîner avec des exercices résolus étape par étape sur les dérivées appliquant la règle de la chaîne.
Quelle est la règle de la chaîne ?
La règle de chaîne est une formule utilisée pour dériver des fonctions composites. La règle de la chaîne stipule que la dérivée d’une fonction composite f(g(x)) est égale à la dérivée f'(g(x)) multipliée par la dérivée g'(x) .
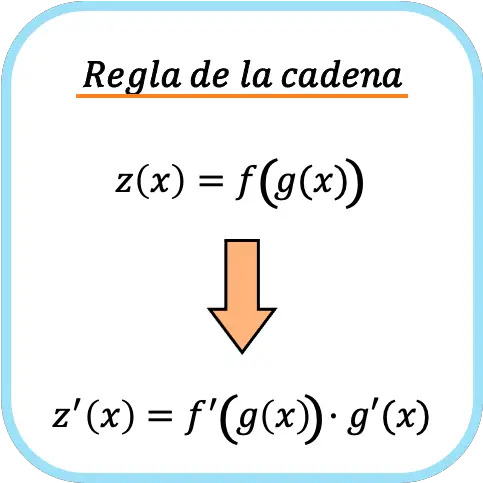
➤ Voir : fonction composite
De manière informelle, on dit souvent que la règle de la chaîne consiste à différencier la fonction puis à la multiplier par ce qu’elle contient .
La formule de la règle de chaîne nous permet de différencier beaucoup plus facilement les fonctions composées, car si nous devions différencier une composition de fonctions en utilisant la limite de la définition de la dérivée, nous devrions faire beaucoup de calculs.
Par contre, il faut tenir compte du fait que cette règle ne sert qu’à trouver la dérivée de fonctions composées, et non d’aucun type de fonction ou d’opérations avec des fonctions. Par exemple, une erreur très courante consiste à se tromper et à appliquer la règle de la chaîne dans des produits fonctionnels comme les suivants :
![]() ❌
❌
La règle de chaîne ne peut être utilisée que lorsque nous avons une fonction à l’intérieur d’une autre .
![]() ✅
✅
Exemples de dérivés avec la règle de la chaîne
Compte tenu de la définition de la règle de chaîne, nous allons dériver plusieurs fonctions avec la règle de chaîne comme exemple. N’oubliez pas que si dans un exemple vous ne comprenez pas comment la fonction est dérivée avec la règle de chaîne, vous pouvez nous le demander dans les commentaires !
Exemple 1
Dans cet exemple, nous utiliserons la règle de la chaîne pour dériver le logarithme népérien de x au carré :
![]()
La dérivée du logarithme népérien est égale à 1 fois son argument, donc la dérivée
![]() être:
être:
![]()
![]()
En revanche, la dérivée de x élevée à la puissance deux est 2x :
![]()
Enfin, nous calculons la dérivée de la fonction entière en appliquant la règle de la chaîne. La dérivée de la fonction composite sera le produit des deux dérivées que l’on vient de trouver :
![]()
![]()
Exemple 2
Dans ce deuxième exemple, nous dériverons une fonction potentielle basée sur un polynôme :
![]()
Pour dériver une puissance, nous devons placer l’exposant d’origine devant et soustraire une unité à l’exposant, donc la dérivée de la fonction potentielle sans appliquer la règle de la chaîne serait :
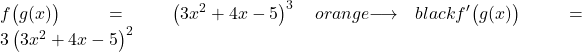
Maintenant, nous déduisons ce qui est entre parenthèses :
![]()
Et enfin, on utilise la règle de la chaîne pour résoudre la dérivée de la fonction entière, qui sera la multiplication des deux dérivées calculées précédemment :
![]()
![]()
Exemple 3
Dans ce cas, nous résoudrons la dérivée du sinus de x au cube plus 7x :
![]()
En effet, il s’agit d’une composition de fonctions car on a la fonction x 3 +7x à l’intérieur de la fonction sinus, on peut donc utiliser la règle de la chaîne pour trouver la dérivée de la fonction composite.
D’une part, la dérivée du sinus est le cosinus, donc la dérivée de la fonction extérieure sera le cosinus avec le même argument que le sinus :
![]()
Et d’autre part, la dérivée de x 3 +7x est 3x 2 +7.
![]()
Par conséquent, la dérivée de la fonction composite est le produit des deux dérivées :
![]()
![]()
Exercices résolus sur les dérivés avec la règle de la chaîne
Exercice 1
Dérivez la fonction composite suivante à l’aide de la règle de chaîne :
![]()
La fonction extérieure est une fonction potentielle, donc pour calculer sa dérivée il faut appliquer la formule suivante :
![]()
![]()
Et puis nous calculons la dérivée de la fonction à l’intérieur. C’est une soustraction de puissances, donc pour calculer sa dérivée il faut appliquer la formule suivante à chacun de ses termes :
![]()
![]()
![]()
En bref, la dérivée de la fonction composite est le produit des deux dérivées trouvées :
![]()
![]()
Exercice 2
Résolvez la dérivée de la fonction composite suivante à l’aide de la règle de chaîne :
![]()
Tout d’abord, on trouve la dérivée de la fonction extérieure :
![Rendered by QuickLaTeX.com \begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e5d21c7196c7ebaeaf6ca11762ca251_l3.png)
Et maintenant nous résolvons la dérivée de la fonction intérieure :
![]()
La dérivée de la fonction entière est donc :
![]()
![]()
Exercice 3
Calculez la dérivée de la composition de fonctions suivante avec la règle de la chaîne :
![]()
C’est une fonction exponentielle, donc pour calculer sa dérivée il faut appliquer la formule suivante :
![]()
![]()
Nous dérivons également la fonction à partir de l’exposant de la fonction :
![]()
Et nous utilisons la règle de la chaîne pour trouver la dérivée de la fonction composée entière :
![]()
![]()
Exercice 4
Trouvez la dérivée de la fonction composite suivante à l’aide de la règle de chaîne :
![]()
Il s’agit d’une composition de fonctions, car nous avons une fonction sinusoïdale et une fonction linéaire dans l’argument d’une fonction irrationnelle. Nous calculons donc d’abord la dérivée de la racine :
![]()
![Rendered by QuickLaTeX.com f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e909efbe50930f94cce0b2485b060046_l3.png)
Et maintenant nous dérivons l’argument du radical. C’est une somme de fonctions, donc la dérivée sera la somme des dérivées de chaque terme :
![]()
Ainsi la dérivée de la fonction entière est égale à la multiplication des deux dérivées calculées :
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fad132b49a5faab86a3955efd5422973_l3.png)
Exercice 5
Dérivez la composition de fonctions suivante à l’aide de la règle de chaîne :
![]()
Pour appliquer la règle de la chaîne, il faut trouver la dérivée de la puissance et du polynôme puis les multiplier. Ainsi, nous dérivons la puissance en utilisant la formule correspondante :
![]()
![]()
Deuxièmement, nous dérivons la fonction polynomiale de l’exposant :
![]()
Et la règle de la chaîne nous dit que la dérivée de la fonction entière est le produit des dérivées que nous venons de trouver :
![]()
![]()
Exercice 6
![]()
Évidemment, la fonction de ce problème est composite, puisque dans l’argument du logarithme népérien nous avons un produit de deux types de fonctions différents. Nous dérivons donc d’abord le logarithme :
![]()
![]()
Deuxièmement, nous dérivons la fonction de l’argument logarithme. Il s’agit d’une multiplication de deux fonctions, il faut donc utiliser la formule suivante pour faire la dérivation :
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-643ddf7ec82cbcc3bc685ceadf59da98_l3.png)
Ainsi, la dérivée de la fonction entière, selon la règle de la chaîne, sera le produit des deux dérivées :
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6912d0951fb85a61df21cbed282000f2_l3.png)
Exercice 7
Résolvez la dérivée de la fonction suivante en utilisant la règle de la chaîne :
![]()
C’est une composition de fonctions, nous allons donc différencier le logarithme et son argument séparément puis multiplier les dérivées.
Donc, d’abord, nous différencions le logarithme en base 9 :
![]()
![]()
Et maintenant, nous calculons la dérivée de l’argument du logarithme. Notez que le nombre e a une fonction dans son argument, c’est-à-dire qu’il s’agit d’une fonction composite, nous devons donc également appliquer la règle de la chaîne pour dériver cette fonction :
![]()
![]()
Ainsi, la dérivée de l’argument entier du logarithme sera :
![]()
Et enfin, la dérivée de la fonction entière sera le produit de f'(g(x)) et g'(x) :
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a702df902c9f1eff66e14836a262c0a_l3.png)
Exercice 8
Dérivez la fonction composite suivante à l’aide de la règle de chaîne :
![]()
Dans cet exercice, nous avons une composition de plusieurs fonctions, nous devrons donc appliquer la règle de la chaîne plusieurs fois. Nous dérivons d’abord la fonction trigonométrique du sinus, dont la dérivée est le cosinus :
![]()
Et maintenant, nous calculons la dérivée de l’argument sinus en utilisant la règle de la chaîne :
![]()
![Rendered by QuickLaTeX.com \begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e1c2492990456e277e493c898cb3924_l3.png)
Enfin, on obtient la dérivée de la composition entière des fonctions en appliquant à nouveau la règle de la chaîne :
![]()
![]()
Preuve de règle de chaîne
Enfin, nous allons prouver la formule de la règle de chaîne. Pour ce faire, nous partirons de la définition mathématique d’une dérivée :
![]()
Soit z une fonction composée de deux fonctions :
![]()
Alors la dérivée de la fonction z appliquant la définition serait :
![]()
Comme vous le savez déjà, on peut multiplier et diviser une fraction par le même terme, car cela ne modifie pas le résultat. Nous pouvons donc passer à l’étape suivante :
![]()
On réorganise les dénominateurs des fractions :
![]()
En appliquant les propriétés des limites, nous pouvons séparer la limite ci-dessus en deux. Puisque la limite d’un produit est égale au produit des limites :
![]()
Et cette expression équivaut à la suivante :
![]()
La formule de la règle de chaîne est donc prouvée, puisque nous y sommes parvenus à partir de la définition de la dérivée.