▷ Quels sont tous les types de discontinuités ?

Vous découvrirez ici quels types de discontinuités existent. De plus, vous pourrez voir des exemples de tous types de discontinuités et vous pourrez vous entraîner avec des exercices résolus sur les types de discontinuités de fonctions.

Quels sont tous les types de discontinuités ?

Il existe trois types de discontinuités, à savoir :

Discontinuité évitable : Les limites latérales d’une fonction en un point ne coïncident pas avec la valeur de la fonction.
Discontinuité de saut fini inévitable : Les limites latérales d’une fonction en un point sont différentes.
Discontinuité de saut infini inévitable : une des limites latérales de la fonction donne l’infini ou n’existe pas.

Pour finir de comprendre les concepts, nous allons expliquer plus en détail chaque type de discontinuité et nous allons voir des exemples de fonctions avec les trois types de discontinuités.

Discontinuité évitable

La discontinuité évitable est un type de discontinuité qui a une fonction en un point si la limite existe en ce point mais qu’elle ne coïncide pas avec la valeur de la fonction ou que l’image de la fonction n’existe pas.

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a) \qquad | \qquad \displaystyle \exists\lim_{x \to a} f(x) \text{ y } \ \cancel{\exists} \ f(a)$

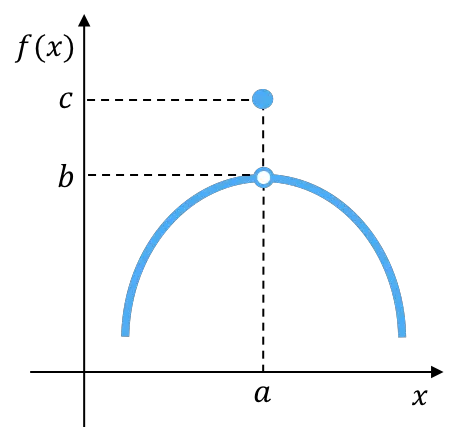
Les limites latérales de cette fonction sont égales les unes aux autres, mais elles sont différentes de la valeur de la fonction en ce point. La fonction présente donc une discontinuité évitable.

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad f(a)=c$

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a)$

discontinuité évitable d'une fonction sans image

La fonction de l’exemple précédent a une discontinuité évitable car les limites latérales en x=a ont la même valeur, mais l’image de la fonction en ce point n’existe pas.

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad \cancel{\exists} \ f(a)$

➤ Voir : limites latérales d’une fonction

Discontinuité inévitable du saut fini

L’ inévitable discontinuité de saut fini est un type de discontinuité qui présente une fonction en un point lorsque les limites latérales de la fonction en ce point ne sont pas égales.

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

Par exemple, les limites latérales de la fonction suivante définie par morceaux au point de changement de définition sont différentes, par conséquent la fonction présente une inévitable discontinuité de saut fini à ce point.

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=c$

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

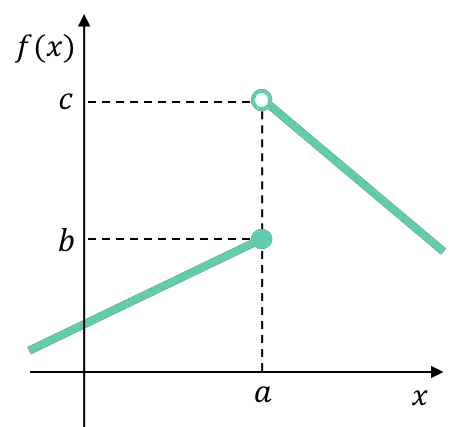
Ce type de discontinuité apparaît généralement dans les fonctions définies par morceaux (ou par morceaux).

➤ Voir : continuité d’une fonction par morceaux

Saut infini Discontinuité inévitable

La discontinuité inévitable du saut infini est un type de discontinuité qui a une fonction à heures si l’une des limites latérales à ce point est infinie ou n’existe pas.

$\displaystyle \lim_{x \to a^-} f(x) = \pm \infty \qquad \lim_{x \to a^+} f(x)= \pm \infty$

La limite gauche de la fonction suivante donne un nombre réel, mais la limite droite donne l’infini. La fonction présente donc une inévitable discontinuité de saut infini.

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=+\infty$

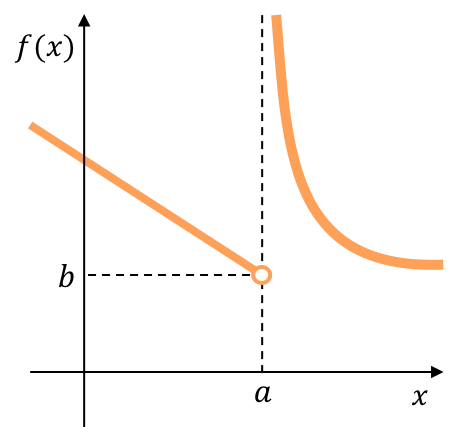
Ci-dessous, vous pouvez voir une fonction graphique dont les deux limites latérales donnent l’infini et donc la fonction a une inévitable discontinuité de saut infinie.

$\displaystyle \lim_{x \to a^-} f(x)=-\infty \qquad \lim_{x \to a^+} f(x)=+\infty$

Ce type de discontinuité se produit généralement dans les fonctions rationnelles (ou fractionnaires) .

Exercices résolus sur les types de discontinuités

Exercice 1

Déterminez le type de discontinuité de la fonction par morceaux suivante au point x=3 :

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.$

Voir la solution

Le domaine du premier élément de la fonction,

$-2x+1$ , comme celui du deuxième morceau, $4x-5$ , sont tous des nombres réels car ce sont des fonctions polynomiales.

Ainsi, le seul point auquel la fonction pourrait être discontinue est le point d’arrêt de la fonction par morceaux. Nous allons donc calculer les limites latérales à ce stade :

$\displaystyle \lim_{x \to 3^-} f(x)=\lim_{x \to 3} (-2x+1) = -2\cdot 3+1=-5$

$\displaystyle \lim_{x \to 3^+} f(x)=\lim_{x \to 3}(4x-5)=4\cdot 3-5=7$

$\displaystyle \lim_{x \to 3^-} f(x) \neq \lim_{x \to 3^+} f(x)$

Les deux limites latérales en x=3 donnent des résultats différents. Par conséquent, le point x=3 est une discontinuité de saut fini inévitable.

Exercice 2

Trouvez quel type de discontinuité la fonction rationnelle suivante présente en des points qui n’appartiennent pas à son domaine :

$f(x)= \cfrac{x^2-4}{x+2}$

Voir la solution

Logiquement, pour résoudre cet exercice, il faut d’abord trouver le domaine de la fonction. Ainsi, puisqu’il s’agit d’une fonction rationnelle, nous fixons le dénominateur égal à 0 et résolvons l’équation résultante :

$x+2=0$

$x=-2$

$\text{Dom } f = \mathbb{R} - \{-2\}$

La fonction sera donc continue en tous points sauf x=-2, voyons donc quel type de discontinuité est le point x=-2. Pour ce faire, on calcule la limite de la fonction au point :

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2} = \cfrac{ (-2)^2-4}{-2+2}= \cfrac{0}{0}$

Mais on obtient une indétermination nulle entre zéro, on factorise donc les polynômes du numérateur et du dénominateur et on simplifie :

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2}=\lim_{x \to -2} \cfrac{ (x-2)\cancel{(x+2)}}{\cancel{x+2}} =\lim_{x \to -2} (x-2)$

Maintenant, nous résolvons la limite :

$\displaystyle \lim_{x \to -2} (x-2) =-2-2=-4$

Par conséquent, la limite de la fonction au point x=-2 existe bien et donne -4. Vérifions maintenant s’il existe

$f(-2):$

$f(-2)=\cfrac{(-2)^2-4}{-2+2}= \cfrac{4-4}{0} = \cfrac{0}{0} \quad \bm{\longrightarrow} \quad \cancel{\exists} \ f(2)$

Dans le calcul de l’image d’une fonction, l’indétermination 0/0 ne peut être simplifiée et n’a pas de solution. Alors

$f(-2)$ n’existe pas.

En conclusion, la limite de la fonction en x=-2 existe, mais

$f(-2)$ Non. Par conséquent, x=-2 est une discontinuité évitable.

Exercice 3

Analyser la continuité de la fonction rationnelle suivante :

$\displaystyle f(x)= \frac{2}{x-5}$

Voir la solution

Pour voir si c’est une fonction continue, il faut d’abord calculer son domaine. Nous fixons donc le dénominateur de la fonction rationnelle égal à zéro pour voir quels points n’appartiennent pas au domaine :

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

La fonction sera donc continue en tous points sauf x=5. Voyons donc quel type de discontinuité x=5 est en calculant la limite à ce point :

$\displaystyle \lim_{x \to 5} \frac{2}{x-5} = \frac{2}{5-5} = \frac{2}{0} = \infty$

On se retrouve avec l’indétermination d’un nombre divisé par 0. On calcule donc les limites latérales de la fonction en x=5 :

$\displaystyle \lim_{x \to 5^{-}} \frac{2}{x-5}=\frac{2}{4,999-5}=\frac{2}{-0}= \bm{-\infty}$

$\displaystyle \lim_{x \to 5^{+}} \frac{2}{x-5}=\frac{2}{5,001-5}=\frac{2}{+0}=\bm{+\infty}$

La limite gauche de la fonction à x=5 donne moins l’infini et la limite droite donne plus l’infini. Par conséquent, la fonction a une discontinuité de saut infinie inévitable en x = 5, puisqu’au moins une limite latérale à ce point tend vers l’infini.

Exercice 4

Déterminez toutes les discontinuités de la fonction par morceaux représentée dans le graphique suivant :

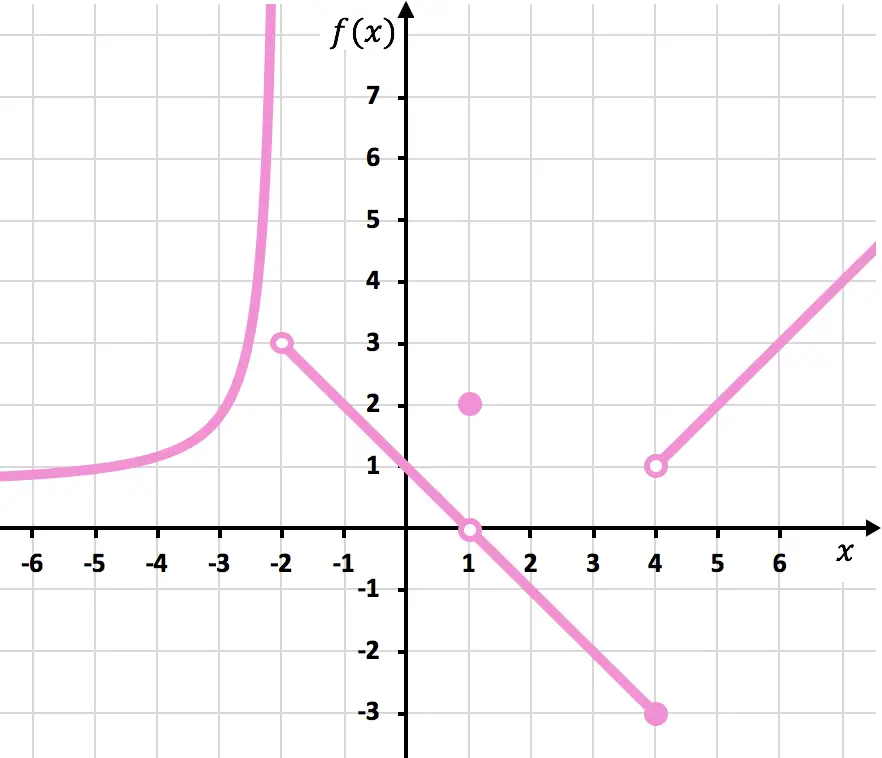
exercice résolu les discontinuités des fonctions

Voir la solution

Pour dessiner la fonction il faut lever le crayon en x=-2, en x=1 et en x=4. La fonction est donc discontinue en ces trois points.

À x=-2, la limite latérale à gauche est +∞ et la limite latérale à droite est 3. Ainsi, puisque l’une des limites latérales est infinie, la fonction a une inévitable discontinuité de saut infini à x=- 2 .

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

La limite de la fonction en x=1 est 0 et, par contre, la valeur de la fonction en x=1 est égale à 2. La fonction présente donc une discontinuité évitable en x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(1) = 2$

À x = 4, la limite latérale à gauche est -3 et la limite latérale à droite est 1. Par conséquent, puisque les deux limites latérales sont différentes et qu’aucune d’elles ne donne l’infini, la fonction a inévitablement une discontinuité de saut fini en x =4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Exercice 5

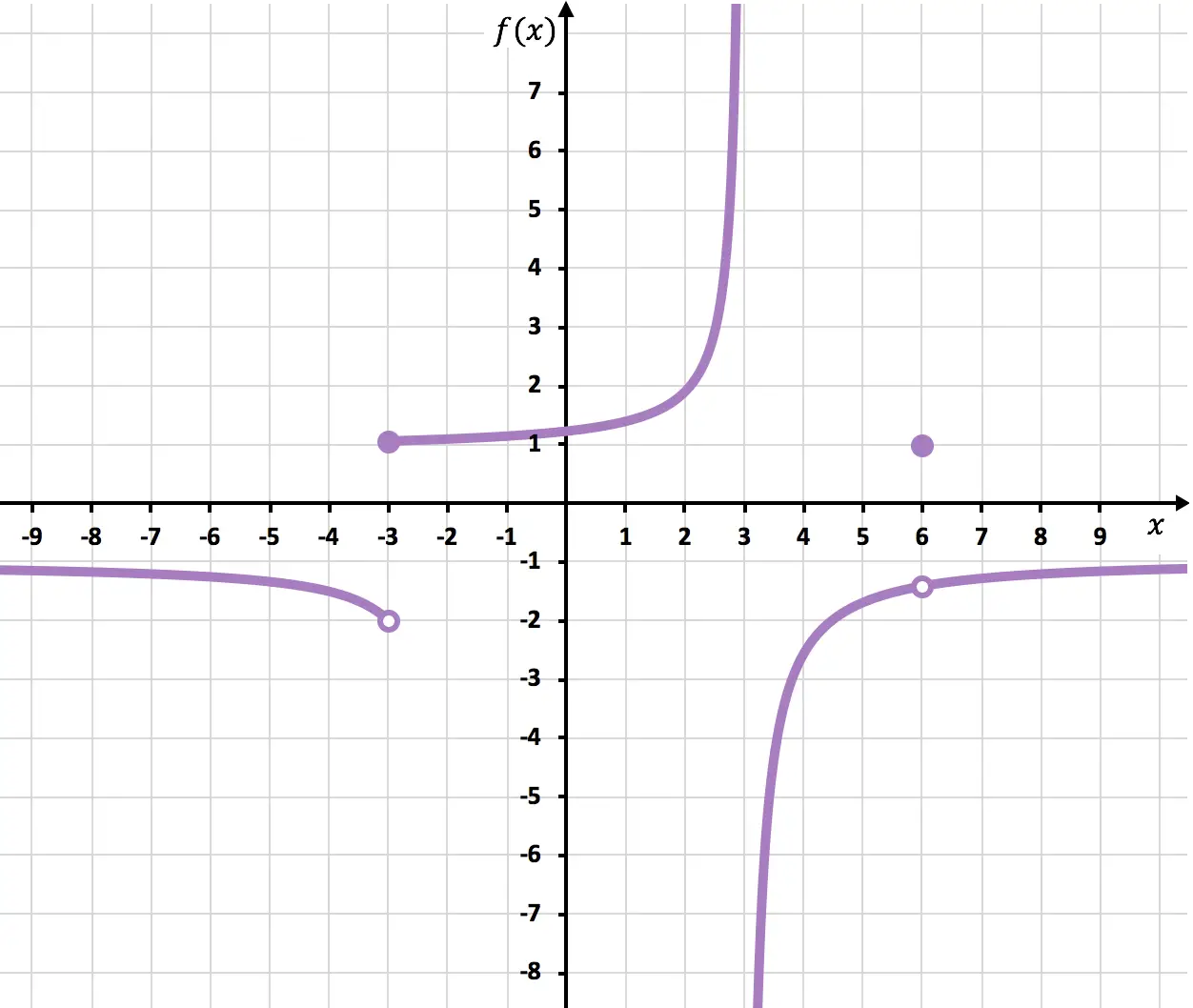
Retrouvez toutes les asymptotes et discontinuités de la fonction représentée dans le graphique suivant :

exercice résolu sur les types de discontinuités d'une fonction

Voir la solution

Asymptotes

La fonction est très proche de la ligne verticale x=3 mais ne la touche jamais. De plus, la limite latérale à gauche en x=3 est +∞ et la limite latérale à droite est -∞. Par conséquent, x=3 est une asymptote verticale.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Et la même chose se produit avec la ligne horizontale y=-1, la fonction se rapproche très près de y=-1 mais ne la traverse jamais. De plus, la limite de la fonction lorsque x tend vers +∞ et -∞ est -1. Par conséquent, y=-1 est une asymptote horizontale.

$\displaystyle \lim_{x \to +\infty} f(x)=-1 \qquad \lim_{x \to -\infty} f(x)=-1$

Discontinuités

A x=6 la fonction est interrompue car il y a un point ouvert. La limite lorsque x s’approche de 6 est -1,4 mais f(6)=1. La fonction a donc une discontinuité évitable en x=6 car la valeur de la limite ne coïncide pas avec la valeur de la fonction :

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

A x=-3 les limites latérales ne coïncident pas et aucune ne donne l’infini. La fonction a donc une inévitable discontinuité de saut fini à x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

Et enfin, la fonction a une inévitable discontinuité de saut infinie en x = 3, puisqu’au moins une limite latérale à ce point aboutit à l’infini.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Types de discontinuités