Limites latérales

Dans cet article, nous expliquons ce qu’est la limite latérale d’une fonction (avec des exemples). Nous vous apprenons également à calculer les limites latérales gauche et droite d’une fonction, à la fois graphiquement et numériquement. De plus, vous pourrez vous entraîner avec des exercices résolus pas à pas de limites latérales.

Quelles sont les limites latérales ?

Les limites latérales d’une fonction en un point étudient le comportement de la fonction autour de ce point. Il y a la limite latérale gauche et la limite latérale droite, qui analysent la valeur de la fonction respectivement à gauche et à droite du point considéré.

Limites latérales à gauche et à droite

Comme nous l’avons vu dans la définition des limites latérales, il en existe deux types : les limites latérales à gauche et les limites latérales à droite.

La limite gauche de la fonction est exprimée par un signe moins au point où la limite est analysée et, d’autre part, la limite droite est indiquée par le signe plus.

Regardez l’exemple suivant pour mieux comprendre la signification des limites latérales :

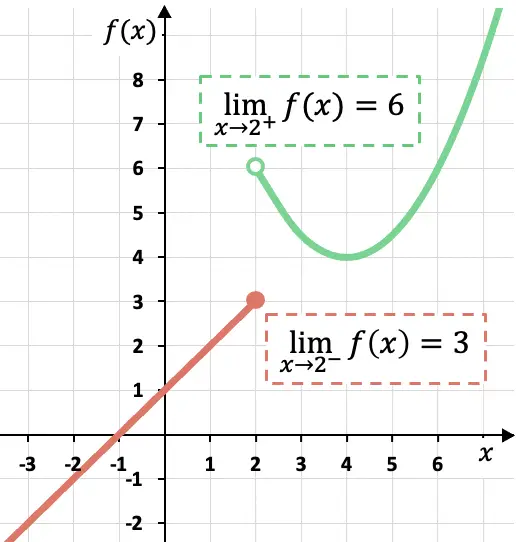
Comme vous pouvez le voir dans la représentation graphique de cette fonction par morceaux, les limites latérales dépendent du côté sur lequel elles sont calculées.

Dans ce cas, la fonction s’approche de 3 lorsque x s’approche de 2 depuis la gauche, puisque la fonction prend des valeurs plus proches de 3 lorsque x s’approche de x=2 depuis sa gauche.

Par contre, la limite latérale de la fonction en x=2 par la droite vaut 6. Car si on approche le point x=2 par sa droite, la fonction prend des valeurs de plus en plus proches de f(x)= 6.

Par contre, il faut savoir que les limites latérales ont les mêmes propriétés que les limites ordinaires. Dans le lien suivant, vous pouvez voir quelles sont les propriétés des limites :

➤ Voir : propriétés des limites

limites latérales égales

Nous venons de voir un exemple où les limites latérales d’une fonction sont différentes, mais… que se passe-t-il si les limites latérales sont les mêmes ?

Si les deux limites latérales d’une fonction en un point existent et sont égales , la limite de la fonction existe en ce point et le résultat de la limite est la valeur des limites latérales.

Autrement dit, pour que la limite d’une fonction existe en un point, la condition suivante doit être remplie :

Par conséquent, si les limites latérales d’une fonction en un point sont différentes, la limite de la fonction en ce point n’existe pas.

Aussi, que la limite d’une fonction en un point existe est une condition essentielle pour qu’elle soit une fonction continue en un point .

Résolvons un exemple pour finir de comprendre le concept de limites latérales :

Les limites latérales au point x=-2 de la fonction représentée graphiquement coïncident, puisque la valeur de la fonction tend vers 3 que l’on s’approche de x=-2 par la gauche ou par la droite. Par conséquent, la limite de la fonction en x=-2 est égale à 3.

Par contre, au point x=4 les limites latérales sont différentes, puisque de la gauche la fonction se rapproche de f(x)=3 mais de la droite la fonction se rapproche de f(x)=2. La limite de la fonction en ce point n’existe donc pas.

Calcul des limites latérales

Compte tenu de la définition des limites latérales, nous allons voir comment elles sont calculées numériquement en résolvant l’exemple suivant :

Si nous calculons la limite comme d’habitude, nous obtenons l’indétermination d’un nombre réel divisé par 0 :

Cependant, lors du calcul des limites latérales, nous n’obtenons aucune indétermination.

Pour calculer la limite latérale de la fonction depuis la gauche en x=2, il faut prendre un nombre plus petit que x=2 mais très proche de celui-ci, par exemple x=1,999.

Dans ce cas, le dénominateur sera un nombre négatif avec une très petite valeur mais même pas zéro, et est généralement représenté par un zéro et un signe moins devant :

Par conséquent, le résultat de la limite latérale est moins l’infini, car tout nombre divisé par 0 donne l’infini, et le positif divisé par le négatif donne le négatif :

On peut vérifier que la fonction tend vers moins l’infini en calculant des images de la fonction avec des valeurs plus proches de x=2 à partir de la gauche.

De même, pour trouver la limite de la fonction au point x=2 à droite, on peut appliquer le même raisonnement : on prend une valeur supérieure à 2 mais très proche, comme 2001.

De la même manière, on peut vérifier que la fonction tend vers plus l’infini en calculant des images de la fonction avec des valeurs de plus en plus proches de x=2 à partir de la droite.

Dans le graphique suivant, vous pouvez voir représentée la fonction analysée. Comme vous pouvez le voir, la limite latérale de la fonction au point x=2 à gauche est moins l’infini, et la limite latérale de la fonction au point x=2 à droite est plus l’infini.

Problèmes de limites latérales résolus

Exercice 1

Trouvez les limites latérales de la fonction définie par morceaux suivante aux points où la définition change (x=-2 et x=4).

Les limites latérales ne coïncident pas au point x=-2, à gauche la fonction tend vers f(x)=5 et, par contre, à droite la fonction est constante et vaut 3.

Les limites latérales sont également différentes lorsque x s’approche de 4. La fonction par morceaux s’approche de 3 à partir de la gauche, mais s’approche de -2 à partir de la droite.

Exercice 2

Déterminez si la limite existe lorsque x s’approche de 3 de la fonction par morceaux suivante, et si oui, quelle est sa valeur.

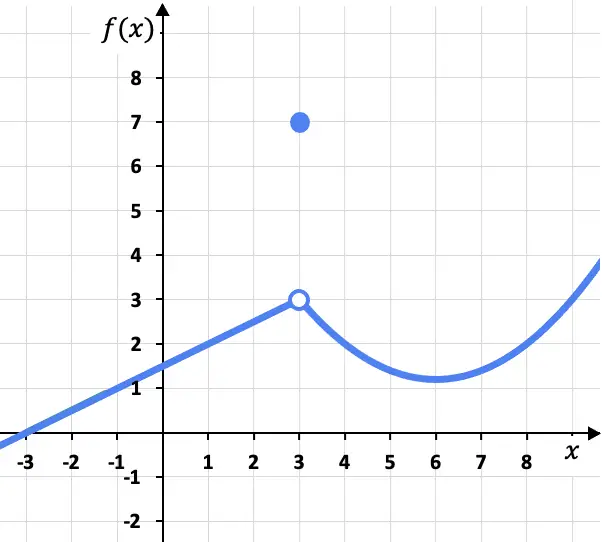
Dans ce problème, les limites latérales au point x=3 par la gauche et par la droite sont identiques, puisque la fonction tend vers la même valeur (f(x)=3) que l’on l’approche par sa gauche ou par sa droite côté:

Par conséquent, selon la définition mathématique de la limite, la limite de la fonction lorsque x tend vers 3 est égale à 3, car les deux limites latérales en ce même point coïncident à cette valeur :

Bien que la limite de la fonction en x=3 soit 3, il faut tenir compte du fait que la fonction en ce point ne vaut pas 3, mais que f(3)=7. Comme nous le verrons plus loin, cela signifie que la fonction n’est pas continue en x=3, mais présente plutôt une discontinuité évitable.

Exercice 3

Calculer les limites latérales de la fonction rationnelle suivante au point x=4.

Pour calculer la limite lorsque x tend vers 4 depuis la gauche, on prend une valeur inférieure à 4 mais très proche de celle-ci, par exemple 3 999 :

Ainsi, la limite latérale lorsque x s’approche de 4 à partir de la gauche est plus l’infini.

Et pour résoudre la limite lorsque x tend vers 4 par la droite, on évalue la fonction à une valeur supérieure à 4 mais très proche de celle-ci, par exemple 4 001 :

Ainsi, la limite latérale lorsque x s’approche de 4 à partir de la droite est moins l’infini.

Exercice 4

Trouver la limite, si elle existe, de la fonction par morceaux suivante définie au point x=2 :

Dans ce cas, l’énoncé du problème nous demande de trouver la limite où la fonction par morceaux change d’expression, nous devons donc trouver la limite du côté gauche en utilisant la première expression et la limite du côté droit en utilisant la deuxième expression.

La limite de la fonction en x=2 à gauche coïncide avec la limite de la fonction à droite, donc la limite de la fonction existe et est égale à 1 :