▷ Asymptote oblique d'une fonction (exercices résolus)

Dans cet article, nous expliquons ce que sont les asymptotes obliques d’une fonction. Vous découvrirez quand une fonction a une asymptote oblique et comment elle est calculée. Et, en plus, vous pourrez voir des exemples d’asymptotes obliques et vous entraîner avec des exercices résolus étape par étape.

Qu’est-ce qu’une asymptote oblique ?

L’asymptote oblique d’une fonction est une ligne inclinée dont son graphe se rapproche indéfiniment sans jamais la traverser. Par conséquent, toutes les asymptotes obliques sont des droites d’équation y=mx+n .

La pente et l’origine d’une asymptote oblique sont calculées à l’aide des formules suivantes :

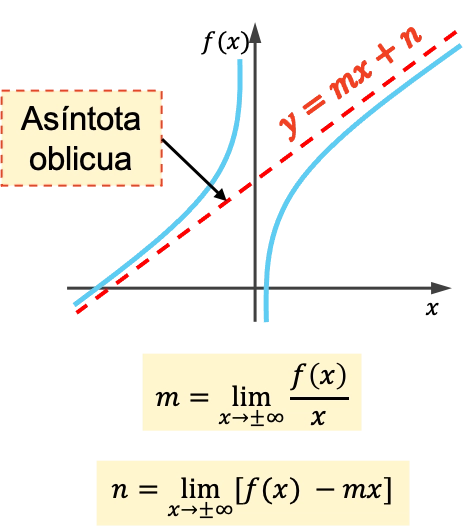
Comment calculer l’asymptote oblique d’une fonction

Pour calculer l’asymptote oblique d’une fonction, les étapes suivantes doivent être effectuées :

Calculez la limite à l’infini de la fonction divisée par x.
Si la limite ci-dessus donne un nombre réel différent de zéro, cela signifie que la fonction a une asymptote oblique. Et de plus, la pente de ladite asymptote oblique sera la valeur obtenue à la limite.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

Dans ce cas, il ne reste plus qu’à calculer l’ordonnée à l’origine de l’asymptote oblique en résolvant la limite suivante :

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Remarque : les limites doivent être calculées à plus et moins l’infini, mais elles donnent normalement le même résultat et c’est pourquoi on simplifie en mettant ±∞. Mais si les limites à plus et moins l’infini étaient différentes, il faudrait calculer séparément l’asymptote oblique à gauche et l’asymptote oblique à droite.

Exemple d’asymptote oblique

Ensuite, nous allons prendre l’asymptote oblique de la fonction rationnelle suivante afin que vous puissiez voir un exemple de la façon dont cela est fait :

$f(x)=\cfrac{x^2+1}{x}$

Les asymptotes obliques sont du type

$y=mx+n.$ Nous calculons donc d’abord la pente de la droite $m$ avec sa formule correspondante :

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

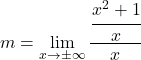
Pour résoudre cette limite il faut appliquer les propriétés des fractions :

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

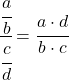
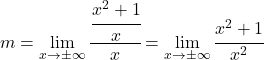
Et maintenant nous calculons la limite :

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

Dans ce cas, le résultat de l’indétermination de l’infini entre l’infini est la division des coefficients des x du plus haut degré, puisque le numérateur et le dénominateur sont du même ordre.

La limite ci-dessus donne un nombre réel non nul, donc la fonction a une asymptote oblique. Nous allons maintenant calculer l’ordonnée à l’origine

$n$ de l’asymptote en utilisant sa formule correspondante :

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

On essaie de calculer la limite :

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Mais nous obtenons l’indétermination infini moins l’infini. Il faut donc réduire les termes à un dénominateur commun. Pour ce faire, on multiplie et divise le x par le dénominateur de la fraction :

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Maintenant que les deux termes ont le même dénominateur, on peut les regrouper :

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

On opère sur le numérateur :

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

Et enfin, nous résolvons la limite :

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Donc n =0. Par conséquent, l’asymptote oblique est une fonction linéaire :

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

La fonction étudiée est représentée dans le graphique ci-dessous. Comme vous pouvez le voir, la fonction se rapproche très près de la droite y=x mais ne la touche jamais car c’est une asymptote oblique :

Exercices résolus sur les asymptotes obliques

Exercice 1

Trouvez l’asymptote oblique de la fonction rationnelle suivante :

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Voir la solution

Les asymptotes obliques sont de la forme

$y=mx+n$ , il faut donc calculer les paramètres m et n . On calcule d’abord m en appliquant sa formule :

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

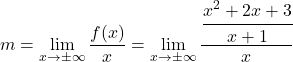
On simplifie la fraction en appliquant les propriétés des fractions :

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

Et on résout la limite :

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Donc m =1. Calculons maintenant l’ordonnée à l’origine de l’asymptote oblique en appliquant sa formule :

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

On essaie de calculer la limite :

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Mais nous obtenons la forme indéterminée infini moins l’infini. Il faut donc réduire les termes à un dénominateur commun puis les regrouper :

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

Et enfin, nous résolvons la limite :

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

En bref, l’asymptote oblique de la fonction est :

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Exercice 2

Trouvez toutes les asymptotes obliques de la fonction rationnelle suivante :

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Voir la solution

Tout d’abord, nous utilisons la formule de la pente de l’asymptote oblique :

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

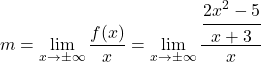
On simplifie la fraction en appliquant les propriétés des fractions :

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

Et on détermine la limite :

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

La limite donne un nombre réel différent de zéro, c’est donc une fonction rationnelle avec une asymptote oblique dont la pente est 2.

Calculons maintenant l’ordonnée à l’origine en appliquant la formule correspondante :

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

On essaie de calculer la limite :

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Mais on obtient la différence d’indétermination des infinis. Par conséquent, nous réduisons les termes à un dénominateur commun et opérons ensuite :

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

Et enfin, nous résolvons la limite :

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

En résumé, l’asymptote oblique de la fonction fractionnaire est :

$y = mx+n$

$\bm{y=2x-6}$

Qu’est-ce qu’une asymptote oblique ?

Comment calculer l’asymptote oblique d’une fonction

Exemple d’asymptote oblique

Exercices résolus sur les asymptotes obliques

Exercice 1

Exercice 2

Leave a Comment Cancel Reply