Sur cette page vous découvrirez ce que sont les fonctions logarithmiques et également comment les représenter sur un graphique. De plus, vous verrez toutes ses caractéristiques, comment calculer son domaine et plusieurs exemples pour mieux le comprendre. Enfin, vous pourrez vous entraîner avec des exercices et des problèmes résolus étape par étape sur les fonctions logarithmiques.
Qu’est-ce qu’une fonction logarithmique ?
La définition d’une fonction logarithmique est la suivante :
En mathématiques, les fonctions logarithmiques sont les fonctions dont la variable indépendante x fait partie de l’argument d’un logarithme. Autrement dit, ils sont les suivants :
![]()
Où
![]() C’est nécessairement un nombre réel positif et différent de 1.
C’est nécessairement un nombre réel positif et différent de 1.
Par exemple, la fonction suivante est logarithmique :
![]()
Avant d’aborder les caractéristiques des fonctions logarithmiques, passons brièvement en revue la notion de logarithme :
- Le logarithme de base
 de
de est l’élément auquel le nombre doit être élevé
est l’élément auquel le nombre doit être élevé pour que le résultat soit le nombre
pour que le résultat soit le nombre 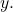
![]()
Rappelons également que le logarithme népérien (ou logarithme népérien) est équivalent au logarithme dont la base est le nombre exponentiel e :
![]()
En revanche, la base est généralement omise lorsqu’elle est 10. Ces types de logarithmes sont appelés logarithmes décimaux ou algorithmes courants :
![]()
Domaine d’une fonction logarithmique
Un logarithme n’admet que des nombres positifs, donc le domaine d’une fonction logarithmique sera tous les nombres qui satisfont à cette condition.
A titre d’exemple, nous allons calculer le domaine de la fonction logarithmique suivante :
![]()
L’argument d’un logarithme doit être supérieur à 0, car il n’existe ni logarithmes de nombres négatifs ni logarithme de 0. Il faut donc regarder quand l’argument de la fonction est supérieur à zéro :
![]()
Maintenant, nous résolvons l’inégalité :
![]()
![]()
![]()
Donc l’argument du logarithme sera supérieur à zéro si
![]() est supérieur à 2. Ainsi, le domaine de la fonction est constitué de tous les nombres supérieurs à 2 (non inclus) :
est supérieur à 2. Ainsi, le domaine de la fonction est constitué de tous les nombres supérieurs à 2 (non inclus) :
![]()
Caractéristiques des fonctions logarithmiques
- Comme nous l’avons vu, le domaine d’une fonction logarithmique est constitué de tous les x qui rendent l’argument du logarithme positif.
- La plage ou la plage d’une fonction logarithmique sont tous des nombres réels.
![]()
- Chaque fonction logarithmique est une fonction continue et injective.
- La croissance ou la diminution d’une fonction logarithmique dépend de la base du logarithme : si la base est supérieure à 1
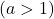 Cependant, la fonction est croissante si la base est comprise dans l’intervalle entre zéro et un.
Cependant, la fonction est croissante si la base est comprise dans l’intervalle entre zéro et un. \bm{\cap}
\bm{\cap} \bm{\cup}
\bm{\cup} f(x)=\log_2 (x-1)
f(x)=\log_2 (x-1)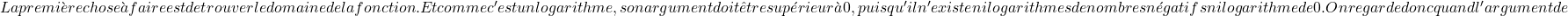 \log_2 (x-1)
\log_2 (x-1)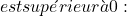 x-1>0x>1
x-1>0x>1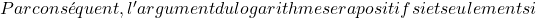 x
x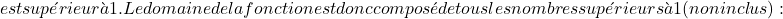 \text{Dom } f = (1,+\infty)
\text{Dom } f = (1,+\infty) x= 1,5 \ \longrightarrow \ f(1,5)=\log_2 (1,5-1)=-1
x= 1,5 \ \longrightarrow \ f(1,5)=\log_2 (1,5-1)=-1 x= 2 \ \longrightarrow \ f(2)=\log_2 (2-1)= 0
x= 2 \ \longrightarrow \ f(2)=\log_2 (2-1)= 0 x= 3 \ \longrightarrow \ f(3)=\log_2 (3-1) = 1
x= 3 \ \longrightarrow \ f(3)=\log_2 (3-1) = 1 x= 5 \ \longrightarrow \ f(5)=\log_2 (5-1) = 2
x= 5 \ \longrightarrow \ f(5)=\log_2 (5-1) = 2 x= 9 \ \longrightarrow \ f(9)=\log_2 (9-1) = 3
x= 9 \ \longrightarrow \ f(9)=\log_2 (9-1) = 3 \begin{array}{c|c} x & f(x) \\ \hline 1,5 & -1 \\ 2 & 0 \\ 3 & 1 \\ 5 & 2 \\ 9 & 3 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 1,5 & -1 \\ 2 & 0 \\ 3 & 1 \\ 5 & 2 \\ 9 & 3 \end{array}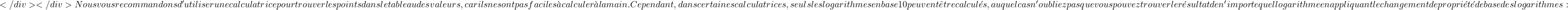 \log_2 0,5 = \cfrac{ \log 0,5 }{ \log 2} = -1
\log_2 0,5 = \cfrac{ \log 0,5 }{ \log 2} = -1 f(x)= \log_8 4x
f(x)= \log_8 4x  4x>0 x>\cfrac{0}{4} x>0 \mathbf{Dom } \ \bm{f = (0,+\infty)}
4x>0 x>\cfrac{0}{4} x>0 \mathbf{Dom } \ \bm{f = (0,+\infty)}  f(x)= \log (4-x)
f(x)= \log (4-x) 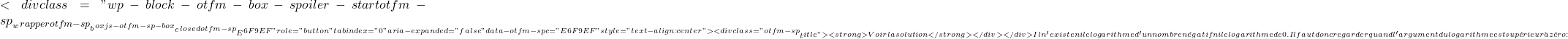 4-x>0-x>-4x<\cfrac{-4}{-1} = 4
4-x>0-x>-4x<\cfrac{-4}{-1} = 4 x<4 \mathbf{Dom } \ \bm{f = (-\infty,4)}
x<4 \mathbf{Dom } \ \bm{f = (-\infty,4)}  f(x)= \log_2 x
f(x)= \log_2 x 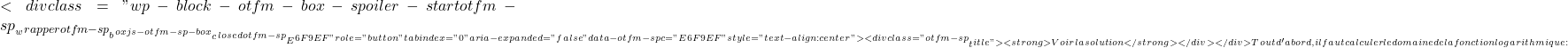 x>0 \text{Dom } f = (0,+\infty)
x>0 \text{Dom } f = (0,+\infty) 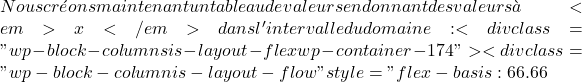 x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 0,5= -1 x= 1 \ \longrightarrow \ f(1)= \log_2 1= 0 x= 2 \ \longrightarrow \ f(2)= \log_2 2= 1 x= 4 \ \longrightarrow \ f(4)= \log_2 4= 2 x= 8 \ \longrightarrow \ f(8)= \log_2 8= 3
x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 0,5= -1 x= 1 \ \longrightarrow \ f(1)= \log_2 1= 0 x= 2 \ \longrightarrow \ f(2)= \log_2 2= 1 x= 4 \ \longrightarrow \ f(4)= \log_2 4= 2 x= 8 \ \longrightarrow \ f(8)= \log_2 8= 3  \begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 1 & 0 \\ 2 & 1 \\ 4 & 2 \\ 8 & 3 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 1 & 0 \\ 2 & 1 \\ 4 & 2 \\ 8 & 3 \end{array} 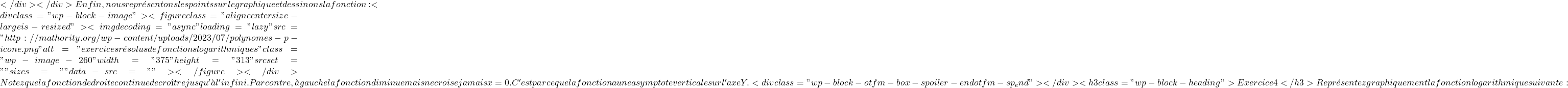 f(x)= \log_2 (x+2)
f(x)= \log_2 (x+2)  x+2>0 x>-2 \text{Dom } f = (-2,+\infty)
x+2>0 x>-2 \text{Dom } f = (-2,+\infty)  x= -1,5 \ \longrightarrow \ f(-1,5)= \log_2 (-1,5+2)= -1 x= -1 \ \longrightarrow \ f(-1)= \log_2 (-1+2)=0 x= 0 \ \longrightarrow \ f(0)=\log_2 (0+2)=1 x= 2 \ \longrightarrow \ f(2)=\log_2 (2+2)=2 x= 6 \ \longrightarrow \ f(6)=\log_2 (6+2)=3
x= -1,5 \ \longrightarrow \ f(-1,5)= \log_2 (-1,5+2)= -1 x= -1 \ \longrightarrow \ f(-1)= \log_2 (-1+2)=0 x= 0 \ \longrightarrow \ f(0)=\log_2 (0+2)=1 x= 2 \ \longrightarrow \ f(2)=\log_2 (2+2)=2 x= 6 \ \longrightarrow \ f(6)=\log_2 (6+2)=3  \begin{array}{c|c} x & f(x) \\ \hline -1,5 & -1 \\ -1 & 0 \\ 0 & 1 \\ 2 & 2 \\ 6 & 3 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline -1,5 & -1 \\ -1 & 0 \\ 0 & 1 \\ 2 & 2 \\ 6 & 3 \end{array}  f(x)=\log_3 x
f(x)=\log_3 x x>0 \text{Dom } f = (0,+\infty)
x>0 \text{Dom } f = (0,+\infty)  x= 1 \ \longrightarrow \ f (1)= \log_3 1= 0 x= 3 \ \longrightarrow \ f(3)= \log_3 3= 1 x= 9 \ \longrightarrow \ f(9)= \log_3 9= 2 \displaystyle x= \cfrac{1}{3} \ \longrightarrow \ f\left( \frac{1}{3} \right)= \log_3 \frac{1}{3}= -1 \displaystyle x= \cfrac{1}{9} \ \longrightarrow \ f\left( \frac{1}{9} \right)= \log_3 \frac{1}{9}= -2
x= 1 \ \longrightarrow \ f (1)= \log_3 1= 0 x= 3 \ \longrightarrow \ f(3)= \log_3 3= 1 x= 9 \ \longrightarrow \ f(9)= \log_3 9= 2 \displaystyle x= \cfrac{1}{3} \ \longrightarrow \ f\left( \frac{1}{3} \right)= \log_3 \frac{1}{3}= -1 \displaystyle x= \cfrac{1}{9} \ \longrightarrow \ f\left( \frac{1}{9} \right)= \log_3 \frac{1}{9}= -2  \begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 3 & 1 \\ 9 & 2 \\ \frac{1}{3} & -1 \\[1.1ex] \frac{1}{9} & -2 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 3 & 1 \\ 9 & 2 \\ \frac{1}{3} & -1 \\[1.1ex] \frac{1}{9} & -2 \end{array}  f(x)= \log_2 (1-x)
f(x)= \log_2 (1-x)  1-x>0-x>-1x<\cfrac{-1}{-1} = 1
1-x>0-x>-1x<\cfrac{-1}{-1} = 1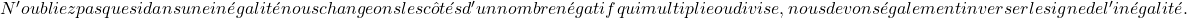 x<1 \text{Dom } f = (-\infty,1)
x<1 \text{Dom } f = (-\infty,1)  x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 (1-0,5)=-1 x= 0 \ \longrightarrow \ f(0)= \log_2 (1-0)= 0 x= -1 \ \longrightarrow \ f(-1)=\log_2 (1-(-1))=1 x= -3 \ \longrightarrow \ f(-3)=\log_2 (1-(-3))=2 x= -7 \ \longrightarrow \ f(-7)=\log_2 (1-(-7))=3
x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 (1-0,5)=-1 x= 0 \ \longrightarrow \ f(0)= \log_2 (1-0)= 0 x= -1 \ \longrightarrow \ f(-1)=\log_2 (1-(-1))=1 x= -3 \ \longrightarrow \ f(-3)=\log_2 (1-(-3))=2 x= -7 \ \longrightarrow \ f(-7)=\log_2 (1-(-7))=3  \begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 0 & 0 \\ -1 & 1 \\ -3 & 2 \\ -7 & 3 \end{array}
\begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 0 & 0 \\ -1 & 1 \\ -3 & 2 \\ -7 & 3 \end{array}  \log(A\cdot B) = \log A + \log B
\log(A\cdot B) = \log A + \log B 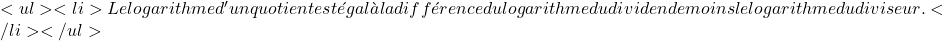 \displaystyle \log \left(\frac{A}{B} \right) = \log A – \log B
\displaystyle \log \left(\frac{A}{B} \right) = \log A – \log B 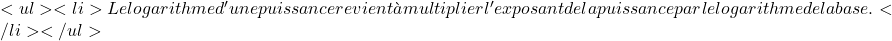 \displaystyle \log A^n = n\cdot \log A
\displaystyle \log A^n = n\cdot \log A 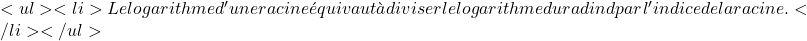 \displaystyle \log \sqrt[n]{A} =\cfrac{\log A}{n} $
\displaystyle \log \sqrt[n]{A} =\cfrac{\log A}{n} $