Sur cette page vous verrez ce qu’est une matrice normale ainsi que des exemples de matrices normales. De plus, vous trouverez les propriétés de ce type de matrices et des exercices résolus pas à pas.
Qu’est-ce qu’une matrice normale ?
La définition de tableau normale est la suivante :
Une matrice normale est une matrice complexe qui multipliée par sa matrice transposée conjuguée est égale au produit de la transposée conjuguée par elle-même.
![]()
Où
![]() est la matrice transposée conjuguée de
est la matrice transposée conjuguée de![]() .
.
Cependant, s’il s’agit de matrices à nombres réels , la condition précédente revient à dire qu’une matrice commute avec sa transposée, c’est-à-dire :
![]()
Car, évidemment, la matrice transposée conjuguée d’une matrice réelle est simplement la matrice transposée (ou transposée).
Exemples de matrices normales
Exemple avec des nombres complexes
La matrice carrée complexe suivante de dimension 2×2 est normale :
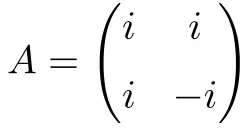
La démonstration de sa normalité est jointe ci-dessous :
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44b98cec879a8332c462d2393fbfbba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fddc406493ac1c81c86edf1ad6e58d0b_l3.png)
Exemple avec des nombres réels
La matrice carrée suivante avec des nombres réels d’ordre 2 est également normale :
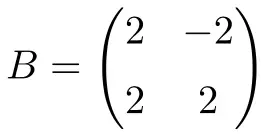
Dans ce cas, puisqu’elle n’a que des nombres réels, pour prouver qu’elle est normale il suffit de vérifier que la matrice est commutable avec sa transposée :
![Rendered by QuickLaTeX.com \displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a320a8e300315c6a48bb8095266408ca_l3.png)
![Rendered by QuickLaTeX.com \displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6ad5bd62deeb5bcbf561a2ee6b29741_l3.png)
Propriétés des matrices normales
Les matrices normales ont les caractéristiques suivantes :
- Toutes les matrices normales sont des matrices diagonalisables.
- Chaque matrice unitaire est aussi une matrice normale.
- De même, une matrice hermitienne est une matrice normale.
- De même, une matrice antihermitienne est une matrice normale.
- Si A est une matrice normale, les valeurs propres (ou valeurs propres) de la matrice transposée conjuguée A* sont les valeurs propres conjuguées de A.
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91ee46b5f8dda0d51ecb57474f5b816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-48c80a017a9afd8b4cf3923757f4e945_l3.png)
- Dans les matrices normales, les vecteurs propres (ou vecteurs propres) associés aux différentes valeurs propres sont orthogonaux.
- Si une matrice est composée uniquement de nombres réels et est symétrique , c’est en même temps une matrice normale.
- De même, une matrice réelle antisymétrique est aussi une matrice normale.
- Enfin, toute matrice orthogonale formée de nombres réels est aussi une matrice normale.
Exercices résolus de matrices normales
Exercice 1
Vérifiez que la matrice complexe suivante de dimension 2 × 2 est normale :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff27d19373c5a4dc8e95472ec295c657_l3.png)
Pour montrer que la matrice est normale il faut d’abord calculer sa transposée conjuguée :
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17c96c654ce5b978f90a905b973d5ae7_l3.png)
Et maintenant on fait la vérification en multipliant la matrice A par la matrice A* dans les deux sens possibles :
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36212e1d12cf35ea5dd27bd91d77ee56_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3db0fc8fdc948037452b4c6275896686_l3.png)
Le résultat des deux multiplications est le même, donc la matrice A est normale.
Exercice 2
Montrer que la matrice réelle suivante de taille 2 × 2 est normale :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854e13859be417985691b5ed6d2a050f_l3.png)
Puisque dans ce cas on a affaire à un environnement avec uniquement des nombres réels, il suffit de vérifier que le produit matriciel entre la matrice A et sa transposée donne le même résultat quel que soit le sens de la multiplication :
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1b6314188f394b3053d3dac0613cf5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2b33f892cd29c0ee232b88eaa4946cc_l3.png)
Le résultat des deux produits est le même, donc la matrice A est normale.
Exercice 3
Déterminez si la matrice suivante de nombres complexes d’ordre 2 est normale :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00075db37b045e08349f7d5b3f679570_l3.png)
Pour vérifier que la matrice est normale, il faut d’abord calculer sa transposée conjuguée :
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0b39733376eb2aef269012eb1d6c24be_l3.png)
Et maintenant on vérifie si la matrice A et sa transposée conjuguée sont commutables :
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c207cb9842dacbaf9bc59d4aaff00473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bcf52f3da81fd7c56b090604c2b6f368_l3.png)
Le résultat des deux multiplications est le même, donc la matrice A est normale.
Exercice 4
Vérifiez que la matrice réelle suivante de dimension 3×3 est normale :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92ee07759c3e6e88af5a68479b5833ea_l3.png)
La matrice étant entièrement composée d’éléments réels, il suffit de vérifier que le produit matriciel entre la matrice A et sa transposée est indépendant du sens de la multiplication :
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc7ee02c75239b430c7fc2418f43e343_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e661b877ee225983c797584e2b61d429_l3.png)
Le résultat des deux produits est le même, donc la matrice A est normale.
Exercice 5
Déterminez si la matrice complexe suivante d’ordre 3×3 est normale :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81ca0ac1da07c151a62dcfb06b4be877_l3.png)
Tout d’abord, nous calculons la transposée conjuguée de la matrice :
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd0a2dfe1b8bfe18020ab68c1eb3bda6_l3.png)
Maintenant, nous devons faire les multiplications matricielles entre la matrice A et sa transposée conjuguée dans les deux sens possibles. Cependant, la matrice transposée conjuguée de A est égale à la matrice A elle-même, il s’agit donc d’une matrice hermitienne. Et par conséquent, des propriétés des matrices normales, il résulte que A est une matrice normale , car toute matrice hermitienne est une matrice normale.