Matrice antisymétrique

Sur cette page, nous expliquons ce que sont les matrices antisymétriques. De plus, vous pourrez voir plusieurs exemples ainsi que sa structure typique pour le comprendre parfaitement. Nous expliquons également la particularité du calcul du déterminant d’une matrice antisymétrique et toutes les propriétés de ce type de matrice. Et enfin, vous découvrirez comment décomposer n’importe quelle matrice carrée en la somme d’une matrice symétrique plus une autre matrice antisymétrique.

Qu’est-ce qu’une matrice antisymétrique ?

La définition de matrice antisymétrique est la suivante :

Une matrice antisymétrique est une matrice carrée dont la transposée est égale au négatif de la matrice.

$A^t = -A$

Où

$A^t$ représente la matrice transposée de $A$ et $-A$ est la matrice $A$ avec tous ses éléments changés de signe.

Exemples de matrices antisymétriques

Une fois que nous connaissons le concept de matrice antisymétrique, nous allons voir plusieurs exemples de matrices antisymétriques pour mieux le comprendre :

Exemple de matrice antisymétrique d’ordre 2 × 2

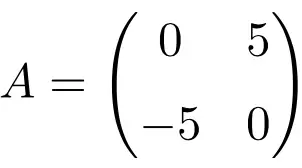
exemple de matrice antisymétrique de dimension 2x2

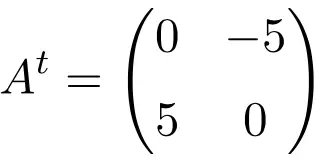
exercice résolu de matrice antisymétrique de dimension 2x2

Exemple de matrice antisymétrique de dimension 3×3

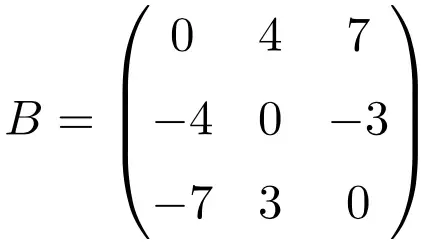
exemple de matrice antisymétrique de dimension 3x3

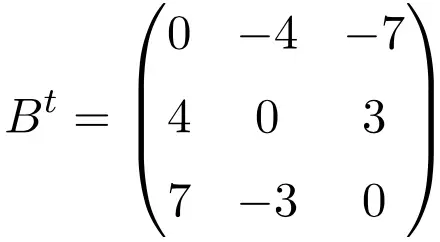
exercice résolu de matrice antisymétrique de dimension 3x3

Exemple de matrice antisymétrique de taille 4×4

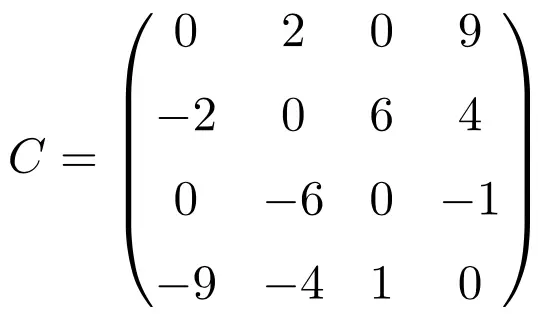
exemple de matrice antisymétrique de dimension 4x4

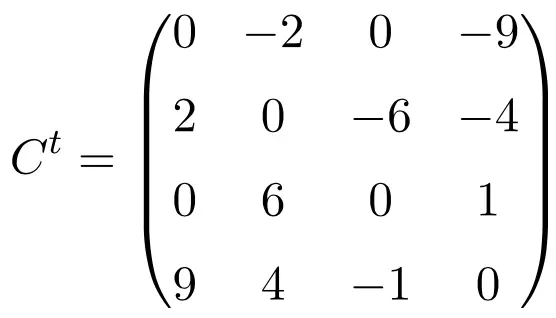
exercice résolu de matrice antisymétrique de dimension 4x4

Lors de la transposition de ces trois matrices, on vérifie qu’elles sont antisymétriques, car les matrices transposées sont équivalentes à leurs matrices d’origine respectives changées de signe.

Structure d’une matrice antisymétrique

Pour que la condition de matrice antisymétrique soit remplie, il faut qu’elles aient toujours le même type de structure : les nombres sur la diagonale principale sont tous égaux à zéro et l’élément de ligne i et de colonne j est le négatif de l’élément de ligne j et de colonne je . Autrement dit, la forme des matrices antisymétriques est la suivante :

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Par conséquent, la diagonale principale d’une matrice antisymétrique agit comme l’axe d’antisymétrie. C’est de là que vient le nom de cette matrice particulière.

Déterminant d’une matrice antisymétrique

Le déterminant d’une matrice antisymétrique dépend de la dimension de ladite matrice. Ceci est dû aux propriétés des déterminants :

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Ainsi, si la matrice antisymétrique est d’ordre impair, son déterminant sera égal à 0 . En revanche, si la matrice antisymétrique est de dimension paire, le déterminant peut prendre n’importe quelle valeur.

Par conséquent, une matrice antisymétrique de dimension impaire est une matrice singulière ou dégénérée. En revanche, une matrice antisymétrique d’ordre pair est une matrice régulière.

Propriétés des matrices antisymétriques

Les caractéristiques des matrices antisymétriques sont les suivantes :

L’addition (ou la soustraction) de deux matrices antisymétriques donne une autre matrice antisymétrique. Puisque transposer deux matrices ajoutées (ou soustraites) équivaut à transposer chaque matrice séparément :

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Toute matrice antisymétrique multipliée par un scalaire donne également naissance à une autre matrice antisymétrique.

La puissance d’une matrice antisymétrique est équivalente à une matrice antisymétrique ou à une matrice symétrique. Si l’exposant est un nombre pair, le résultat de la puissance est une matrice symétrique, mais si l’exposant est un nombre impair, le résultat de la puissance est une matrice antisymétrique. Vous pouvez consulter dans ce lien ce qu’est une matrice symétrique .

La trace d’une matrice antisymétrique est toujours égale à zéro.

La somme de toute matrice antisymétrique plus la matrice unitaire donne lieu à une matrice inversible.

$\displaystyle \text{det}(A+I)\neq 0$

Toutes les valeurs propres réelles (ou valeurs propres) d’une matrice antisymétrique sont 0. Cependant, une matrice antisymétrique peut aussi avoir des valeurs propres complexes.

Toutes les matrices antisymétriques sont des matrices normales. Par conséquent, ils sont soumis au théorème spectral, qui dit qu’une matrice antisymétrique peut être diagonalisée par une matrice unitaire.

Décomposition d’une matrice carrée en une matrice symétrique et une matrice antisymétrique

Une particularité des matrices carrées est qu’elles peuvent être décomposées en la somme d’une matrice symétrique plus une matrice antisymétrique.

La formule qui nous permet de faire cela est la suivante :

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Où C est la matrice carrée que l’on veut décomposer, C ^t sa transposée, et enfin S et A sont respectivement les matrices symétrique et antisymétrique en lesquelles la matrice C est décomposée.

Ci-dessous, vous avez un exercice résolu pour démontrer la formule. Décomposons la matrice suivante :

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

Nous calculons la matrice symétrique et antisymétrique avec les formules :

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

Et nous pouvons vérifier que l’équation est remplie en ajoutant les deux matrices :

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$ ✅