Matrice symétrique

Sur cette page, vous trouverez l’explication de ce que sont les matrices symétriques. De plus, nous vous montrons comment identifier rapidement quand une matrice est symétrique, ainsi que plusieurs exemples pour que vous n’ayez aucun doute. Vous trouverez également toutes les propriétés des matrices symétriques. Et enfin, nous expliquons une particularité particulière que possède toute matrice carrée : elle peut être décomposée en la somme d’une matrice symétrique et d’une matrice antisymétrique.

Qu’est-ce qu’une matrice symétrique ?

La définition d’une matrice symétrique est la suivante :

Une matrice symétrique est une matrice carrée dont la transposée est égale à la matrice elle-même.

$A^t = A$

Où

$A^t$ représente la matrice transposée de $A$ .

Une fois que nous connaissons le concept de matrice symétrique, nous allons voir comment toute matrice symétrique peut être facilement identifiée :

Quand une matrice est-elle symétrique ?

Reconnaître la structure d’une matrice symétrique est très simple : l’élément de ligne i et de colonne j doit être identique à l’élément de ligne j et de colonne i . Et les valeurs de la diagonale principale de la matrice peuvent être quelconques.

Exemples de matrices symétriques

Voici plusieurs exemples de matrices symétriques pour finir de comprendre :

Exemple de matrice symétrique d’ordre 2 × 2

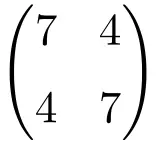
exemple de matrice symétrique de dimension 2x2

Exemple de matrice symétrique de dimension 3×3

exemple de matrice symétrique de dimension 3x3

Exemple de matrice symétrique de taille 4×4

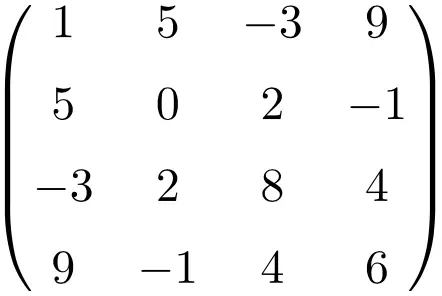
exemple de matrice symétrique de dimension 4x4

En transposant ces trois matrices on vérifie qu’elles sont symétriques, car les matrices transposées sont équivalentes à leurs matrices d’origine respectives.

Pourquoi est-ce appelé une matrice symétrique?

Si vous regardez attentivement les exemples précédents, la diagonale principale d’une matrice symétrique est un axe de symétrie, ou en d’autres termes, elle agit comme un miroir entre les nombres au-dessus de la diagonale et ceux en dessous. Pour cette raison, ces types de matrices sont appelés symétriques.

Propriétés des matrices symétriques

Les caractéristiques des matrices symétriques sont les suivantes :

L’addition (ou la soustraction) de deux matrices symétriques donne une autre matrice symétrique. Puisque transposer deux matrices ajoutées (ou soustraites) équivaut à transposer chaque matrice séparément :

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Toute matrice symétrique multipliée par un scalaire donne également lieu à une autre matrice symétrique.

De même, le produit matriciel entre deux matrices symétriques n’est pas toujours égal à une autre matrice symétrique, seulement si et seulement si les deux matrices peuvent être commuées. Cette condition peut être prouvée avec la propriété de multiplication matricielle transposée :

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

La puissance d’une matrice symétrique donne naissance à une autre matrice symétrique, tant que l’exposant est un entier.

Évidemment, la matrice unitaire et la matrice nulle sont des exemples de matrices symétriques.

Une matrice congruente à une matrice symétrique doit également être symétrique.

Si une matrice symétrique est régulière ou inversible, alors sa matrice inverse est également symétrique.

Il en va de même avec l’adjoint d’une matrice symétrique : la matrice adjointe d’une matrice symétrique donne comme solution une autre matrice symétrique.

Une vraie matrice symétrique est aussi une matrice normale.

Les matrices symétriques étant un cas particulier des matrices hermitiennes, toutes les valeurs propres (ou valeurs propres) d’une matrice symétrique sont des nombres réels.

Le théorème spectral nous dit que toutes les matrices dont les éléments sont réels sont des matrices diagonalisables et, de plus, la diagonalisation s’effectue au moyen d’une matrice orthogonale. Par conséquent, toutes les matrices symétriques réelles sont diagonalisées orthogonalement.

D’autre part, les matrices symétriques avec des nombres complexes peuvent être diagonalisées à travers une matrice unitaire.

La matrice hessienne est toujours symétrique.

Décomposition d’une matrice carrée en une matrice symétrique et une matrice antisymétrique

Une particularité des matrices carrées est qu’elles peuvent être décomposées en la somme d’une matrice symétrique plus une matrice antisymétrique.

La formule qui nous permet de faire cela est la suivante :

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Où C est la matrice carrée que l’on veut décomposer, C ^t sa transposée, et enfin S et A sont respectivement les matrices symétrique et antisymétrique en lesquelles la matrice C est décomposée.

Ci-dessous, vous avez un exercice résolu pour voir comment cela se fait. Décomposons la matrice suivante :

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Nous calculons la matrice symétrique et antisymétrique avec les formules :

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

Et nous pouvons vérifier que l’équation est remplie en ajoutant les deux matrices :

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$ ✅