Matrice hermitienne (ou hermitienne)

Sur cette page, vous pouvez apprendre ce qu’est une matrice hermitienne, également connue sous le nom de matrice hermitienne. Vous trouverez des exemples de matrices hermitiennes, toutes leurs propriétés et la forme que possèdent ces types de matrices afin de les comprendre parfaitement. Enfin, nous expliquons également comment décomposer toute matrice complexe en la somme d’une matrice hermitienne plus une matrice anti-hermitienne.

Qu’est-ce qu’une matrice hermitienne ou hermitienne ?

Une matrice hermitienne , ou encore appelée matrice hermitienne, est une matrice carrée à nombres complexes qui a pour caractéristique d’être égale à sa transposée conjuguée .

A=A^*

Où

A^* est la matrice transposée conjuguée deA .

Par curiosité, ce type de matrice est nommé ainsi en l’honneur de Charles Hermite, un mathématicien français du XIXe siècle qui a fait d’importantes recherches en mathématiques, et notamment dans le domaine de l’algèbre linéaire.

La raison de nommer cette matrice de cette façon était qu’il a montré que les valeurs propres (ou valeurs propres) de ces matrices particulières sont toujours des nombres réels, mais nous expliquerons cela plus en détail dans les propriétés des matrices hermitiennes.

Enfin, cette matrice peut aussi parfois être qualifiée de matrice auto-adjointe, bien que cela soit très rare.

Exemples de matrices hermitiennes

Une fois que nous avons vu la définition de la matrice hermitienne (ou matrice hermitienne), voyons quelques exemples de matrices hermitiennes de différentes dimensions :

Exemple de matrice hermitienne d’ordre 2×2

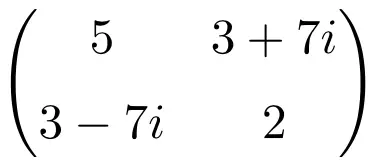
Matrice hermitienne ou hermitienne de dimension 2x2

Exemple de matrice hermitienne de dimension 3 × 3

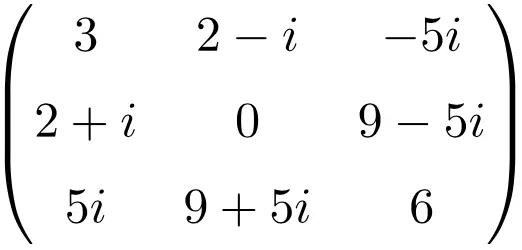
Matrice hermitienne ou hermitienne de dimension 3x3

Exemple de matrice hermitienne de taille 4×4

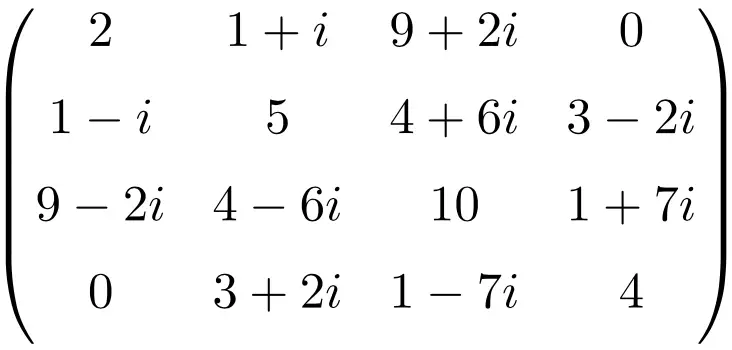
Matrice hermitienne ou hermitienne de dimension 4x4

Toutes ces matrices sont hermitiennes car la matrice transposée conjuguée de chacune est égale à la matrice elle-même.

Structure d’une matrice hermitienne

Les matrices hermitiennes ont une structure très facile à retenir : elles sont constituées de nombres réels sur la diagonale principale, et l’élément complexe situé dans la ième ligne et la jième colonne doit être le conjugué de l’élément qui se trouve dans la j-ième ligne et la ième colonne.

Voici quelques exemples de structures matricielles hermitiennes.

Structure hermitienne 2×2

\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}

Structure hermitienne 3×3

\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}

Structure hermitienne 4×4

\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}

Propriétés de la matrice hermitienne

Nous allons maintenant voir quelles sont les propriétés de ce type de matrice complexe carrée :

  • Toute matrice hermitienne est une matrice normale . Bien que toutes les matrices normales ne soient pas des matrices hermitiennes.
  • Toute matrice hermitienne est diagonalisable. De plus, la matrice diagonale obtenue ne contient que des éléments réels.
  • Par conséquent, les valeurs propres (ou valeurs propres) d’une matrice hermitienne sont toujours des nombres réels. Cette propriété a été découverte par Charles Hermite, et pour cette raison, il a été honoré d’appeler cette matrice très spéciale hermitienne.
  • De même, les espaces propres d’une matrice hermitienne sont orthogonaux deux à deux : il existe une base orthonormée de\mathbb{C}^n constitué de vecteurs propres (vecteurs propres) de la matrice.
  • Une matrice de nombres réels, c’est-à-dire qu’aucun élément n’a de partie imaginaire, est hermitienne si et seulement si c’est une matrice symétrique. Comme par exemple la matrice identité 2×2 .
  • Une matrice hermitienne peut être exprimée comme la somme d’une matrice symétrique réelle et d’une matrice antisymétrique imaginaire.

A =B+Ci

  • La somme (ou soustraction) de deux matrices hermitiennes est égale à une autre matrice hermitienne, car :

(A\pm B)^* = A^*\pm B^* = A \pm B

  • Le résultat du produit d’une matrice hermitienne par un scalaire est une autre matrice hermitienne si le scalaire est un nombre réel.

(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A

  • Le produit de deux matrices hermitiennes n’est généralement plus hermitien. Cependant, le produit est hermitien lorsque les deux matrices sont commutables, c’est-à-dire lorsque le résultat de la multiplication des deux matrices est le même quel que soit le sens dans lequel elles sont multipliées, car alors la condition suivante des opérations avec transposée conjuguée matrices :

(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B

  • Si une matrice hermitienne est inversible, son inverse s’avère également être une matrice hermitienne.

(A^{-1})^* = (A^*)^{-1} = A^{-1}

  • Le déterminant d’une matrice hermitienne est toujours équivalent à un nombre réel. Voici la preuve de cette propriété :

det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}

Donc si

A = A^* :

det(A) = \overline{det(A)}

Donc, pour que cette condition soit remplie, il faut nécessairement que le déterminant d’une matrice hermitienne soit un nombre réel. De cette manière, le conjugué du résultat est égal au résultat lui-même.

Décomposition d’une matrice complexe en une matrice hermitienne et une matrice anti-hermitienne

Toute matrice avec des éléments complexes peut être décomposée en la somme d’une matrice hermitienne plus une autre matrice anti-hermitienne . Mais pour cela il faut connaître les particularités suivantes de ces types de matrices :

  • La somme d’une matrice complexe carrée plus son conjugué transposé donne une matrice hermitienne.

C + C^* = \text{Matriz Hermitiana}

  • La différence entre une matrice complexe carrée et son conjugué transposé donne une matrice anti-hermitienne (ou anti-hermitienne).

C - C^* = \text{Matriz Antihermitiana}

  • Par conséquent, toutes les matrices complexes peuvent être décomposées en la somme d’une matrice hermitienne et d’une matrice anti-hermitienne. Ce théorème est connu sous le nom de décomposition de Teoplitz :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Où C est la matrice complexe que l’on veut décomposer, C* sa conjuguée transposée, et enfin A et B sont respectivement les matrices hermitienne et anti-hermitienne en lesquelles la matrice C est décomposée.

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top