Sur cette page vous verrez ce que sont les matrices complexes, les matrices conjuguées et les matrices transposées conjuguées. Maintenant, ils vous ressemblent beaucoup, mais vous verrez comment à la fin de la page, vous comprendrez parfaitement la différence entre chacun. De plus, nous verrons des exemples de chaque type et de ses propriétés.
matrice complexe
Avant de voir l’explication de la matrice conjuguée et de la matrice conjuguée transposée, passons en revue le concept de matrice complexe :
Qu’est-ce qu’une matrice complexe ?
Une matrice complexe est une matrice qui a un certain nombre complexe parmi ses éléments.
Rappelons qu’un nombre complexe ou imaginaire est un nombre composé d’une partie réelle et d’une partie imaginaire, qui est indiqué par la lettre i. Par exemple:
![]()
.
Exemples de matrices complexes
Regardons quelques exemples de tableaux multidimensionnels complexes :
Exemple de matrice complexe d’ordre 2 × 2
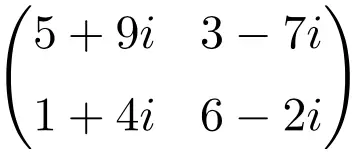
Exemple de matrice complexe de dimension 3×3
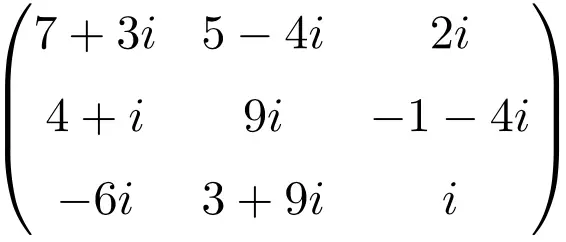
Exemple de matrice complexe de taille 4×4
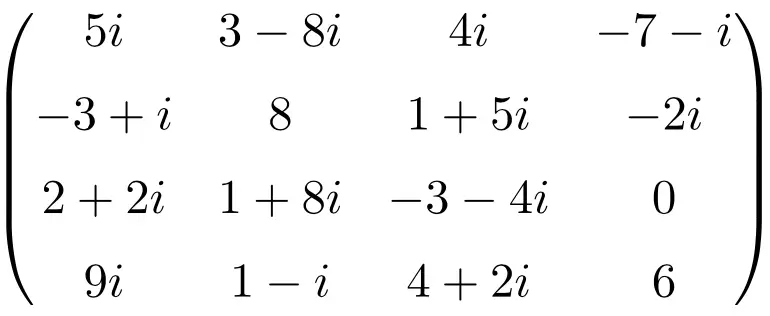
matrice conjuguée
Une fois que nous avons vu quelle est la définition d’une matrice complexe, voyons ce que sont une matrice conjuguée et une matrice conjuguée transposée :
Qu’est-ce qu’une matrice conjuguée ?
Une matrice conjuguée est une matrice complexe dans laquelle tous ses éléments ont été remplacés par leurs conjugués, c’est-à-dire que le signe de la partie imaginaire de tous ses nombres complexes a été modifié.
La matrice conjuguée de
![]() est exprimé par une barre horizontale au-dessus :
est exprimé par une barre horizontale au-dessus :![]() .
.
Exemple de matrice conjuguée
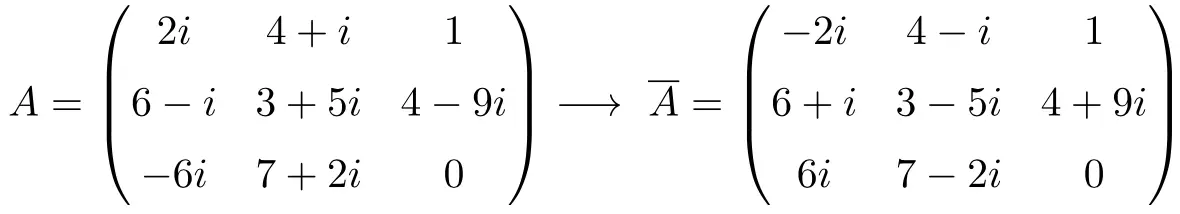
Propriétés de la matrice conjuguée
Les caractéristiques de ce type de matrice sont les suivantes :
- Le conjugué d’une matrice conjuguée est la matrice d’origine.
![]()
- Ajouter (ou soustraire) deux matrices et conjuguer le résultat revient au même que de conjuguer d’abord les deux matrices séparément, puis de les ajouter (ou de les soustraire).
![]()
- Le produit conjugué de deux matrices est égal à la conjugaison des deux matrices séparément, puis au calcul de la multiplication matricielle.
![]()
- Multiplier une matrice par un scalaire et conjuguer le résultat revient au même que de faire d’abord les conjugués du scalaire et de la matrice, puis de résoudre le produit.
![]()
- Transposer une matrice puis la conjuguer revient à conjuguer d’abord la matrice puis à la transposer.
![]()
- Faire l’ inverse d’une matrice puis la conjuguer revient à conjuguer la matrice puis à l’inverser.
![]()
- Le rang d’une matrice conjuguée est égal au rang de la même matrice non conjuguée.
![]()
- Il est indifférent de calculer la trace d’une matrice conjuguée ou de calculer la trace de la même matrice sans conjugaison puis de faire la conjugaison du résultat.
![]()
- Enfin, prendre le déterminant d’une matrice conjuguée revient à calculer le conjugué du résultat du déterminant de la même matrice sans conjugaison.
![]()
Matrice de transposition conjuguée
Enfin, après avoir vu comment conjuguer une matrice, passons au concept de matrice transposée conjuguée :
Qu’est-ce qu’une matrice transposée (ou transposée) conjuguée ?
La matrice transposée (ou transposée) conjuguée est celle obtenue après avoir transposé une matrice puis réalisé sa conjuguée.
Ce type de matrice est aussi appelé matrice adjointe ou simplement matrice adjointe. De plus, il est généralement représenté par un astérisque
![]() , bien qu’il y ait des mathématiciens qui le dessinent comme
, bien qu’il y ait des mathématiciens qui le dessinent comme![]() soit
soit![]() .
.
Exemple de matrice transposée conjuguée
Voici un exemple de calcul de la transposée (ou transposée conjuguée) d’une matrice :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
On fait d’abord la transposition de la matrice A :
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
Et puis on calcule la matrice conjuguée de la transposée, ou en d’autres termes, on change le signe de la partie imaginaire de tous les nombres complexes :
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
Par conséquent, le résumé du calcul de la matrice transposée conjuguée est :
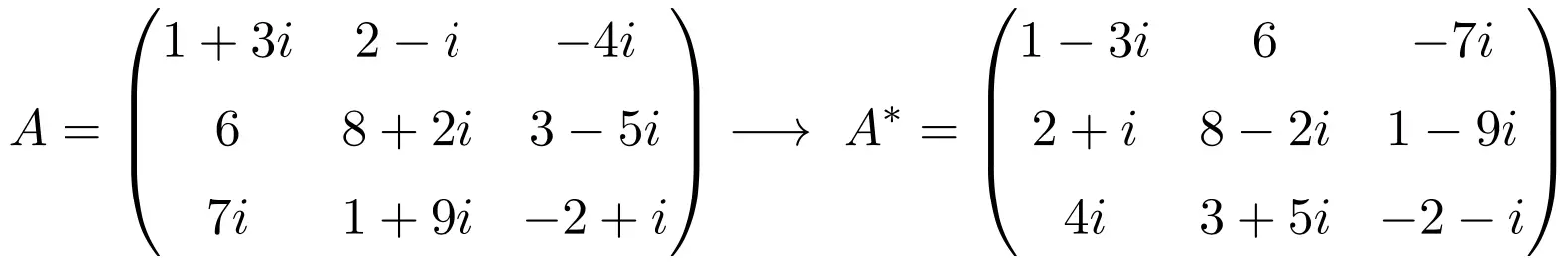
Propriétés de la matrice transposée conjuguée
Les propriétés de ce type de matrice carrée sont les suivantes :
- La matrice transposée conjuguée d’une matrice préalablement transposée et conjuguée est la matrice d’origine.
![]()
- La propriété d’addition des matrices transposées conjuguées indique que faire l’addition (ou la soustraction) de deux matrices puis appliquer cette opération au résultat revient à faire d’abord la transposition conjuguée de chaque matrice puis à ajouter (ou soustraire) les résultats.
![]()
- Multiplier deux matrices puis faire leur transposée conjuguée donne le même résultat que le produit inverse des matrices transposées conjuguées.
![]()
- Le calcul de la matrice transposée conjuguée du produit d’un scalaire et d’une matrice est identique à la conjugaison du nombre complexe et à la recherche séparée de la transposée conjuguée de la matrice, puis à la multiplication.
![]()
- Si la matrice est inversible, l’ordre dans lequel les opérations d’inversion de matrice et de transposition conjuguée sont effectuées est indifférent.
![]()