Sur cette page, nous expliquons ce qu’est la matrice unitaire et, en plus, nous l’illustrons avec plusieurs exercices afin qu’elle soit bien comprise. Vous découvrirez également quelles sont toutes les propriétés de ce type de matrice si important pour l’algèbre linéaire.
Qu’est-ce qu’une matrice unitaire ?
La définition de matrice unitaire est la suivante :
Une matrice unitaire est une matrice complexe qui multipliée par sa matrice transposée conjuguée est égale à la matrice d’identité. C’est-à-dire que la condition suivante est remplie :
![]()
Où
![]() est une matrice unitaire et
est une matrice unitaire et![]() sa transposée conjuguée.
sa transposée conjuguée.
Par conséquent, cette condition implique que l’inverse d’une matrice unitaire est sa transposée conjuguée , car, selon la définition d’une matrice inverse, une matrice est l’inverse d’une autre si son produit est équivalent à la matrice d’identité.
![Rendered by QuickLaTeX.com \left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8f035ef94e00b67acffd2881944642f_l3.png)
Par conséquent, une matrice unitaire sera toujours une matrice régulière ou non dégénérée , puisqu’elle aura toujours un inverse.
Par contre, l’analogue d’une matrice unitaire dans un environnement à nombres réels est la matrice orthogonale , et dans ce cas il est vrai que la matrice unitaire multipliée par sa transposée est égale à la matrice d’identité.
![]()
Donc dans ce cas la matrice inverse de U serait directement sa matrice transposée (ou transposée).
Exemples de matrices unitaires
Exemple de matrice unitaire de dimension 2×2
Une fois que nous avons vu le concept de matrice unitaire, nous allons voir un exemple de matrice unitaire 2×2 pour bien le comprendre :
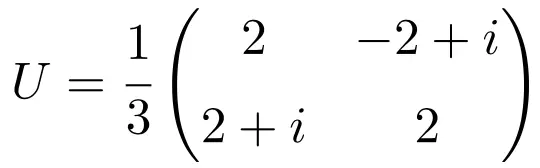
Cette matrice est unitaire car la multiplication d’elle-même par sa matrice conjuguée donne la matrice Identité (ou Unité) :
![Rendered by QuickLaTeX.com \displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11df575022f8a50881fedc994f4f12af_l3.png)
Et, comme nous l’avons vu précédemment, toute matrice unitaire est commutable avec sa transposée conjuguée :
![Rendered by QuickLaTeX.com \displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4848f3eab836be0996049e221bb8a8c3_l3.png)
Exemple de matrice diagonale unitaire
La matrice diagonale composée uniquement du nombre complexe i est également un exemple de matrice unitaire, quelle que soit la dimension de la matrice. Ci-dessous, vous avez un exercice résolu illustrant cela avec une matrice unitaire de dimension 3 × 3 :
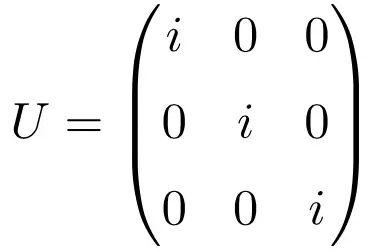
Notez que si nous résolvons le produit de la matrice par sa transposée conjuguée, cela donne la matrice Identité comme solution :
![Rendered by QuickLaTeX.com \displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61bc73f95b9c2515595fe3ed2e18df3f_l3.png)
Et la même chose se produit si nous multiplions les matrices dans le sens inverse :
![Rendered by QuickLaTeX.com \displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cdf7b15d442ec89fde613ba2fd3fe45_l3.png)
La caractéristique de cette matrice est qu’elle sert d’exemple de matrice unitaire de n’importe quelle dimension, puisque chaque fois que la matrice est formée par le nombre imaginaire i sur la diagonale principale et que le reste des éléments sont nuls (0) ce sera une matrice unitaire.
Propriétés d’une matrice unitaire
Les propriétés des matrices unitaires sont les suivantes :
- Évidemment, toute matrice unitaire est une matrice normale . Bien que toutes les matrices normales ne soient pas des matrices unitaires.
- Les matrices unitaires sont toujours des matrices carrées .
- Toutes les matrices unitaires sont diagonalisables, c’est-à-dire qu’elles peuvent être transformées en matrices diagonales.
- La valeur absolue du déterminant d’une matrice unitaire est toujours égale à 1.
![]()
- La matrice identique est une matrice unitaire.
- pour tout entier
 , l’ensemble de toutes les matrices unitaires
, l’ensemble de toutes les matrices unitaires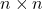 avec l’opération de produit matriciel, ils forment un groupe, appelé groupe unitaire.
avec l’opération de produit matriciel, ils forment un groupe, appelé groupe unitaire.
- De sorte que la multiplication de deux matrices unitaires de même ordre donne une autre matrice unitaire.
- Le module de toutes les valeurs propres (ou valeurs propres) d’une matrice unitaire est toujours égal à 1.
![]()
- Les espaces propres de ce type de matrices sont orthogonaux.