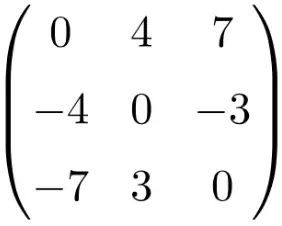Matrice Carrée - Mathority

Sur cette page nous vous expliquons ce qu’est une matrice carrée et vous trouverez des exemples de matrices carrées. De plus, vous verrez quelles sont les propriétés des matrices carrées, les opérations qui peuvent être faites avec elles et les différents types qui existent.

Qu’est-ce qu’une matrice carrée ?

Une matrice carrée est un matrice qui a le même nombre de lignes que de colonnes.

Exemples de matrices carrées

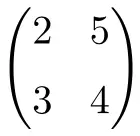
matrice carrée d’ordre 2

matrice carrée d’ordre 3

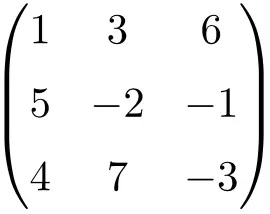
matrice carrée d’ordre 4

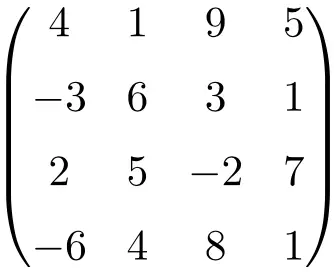
Comme vous pouvez le voir, les matrices carrées sont généralement nommées par leur ordre, c’est-à-dire qu’une matrice carrée d’ordre 2 signifie qu’il s’agit d’une matrice de dimension 2×2 (2 lignes et 2 colonnes), ou alors on parle de matrice carrée d’ordre 3 c’est indiquer qu’il est de taille 3×3 (3 lignes et 3 colonnes).

Diagonales d’une matrice carrée

Les diagonales des matrices carrées ont des noms particuliers, il y a la diagonale principale et la diagonale secondaire :

La diagonale principale d’une matrice carrée est constituée des éléments qui vont du coin supérieur gauche au coin inférieur droit :

diagonale principale d'une matrice carrée

La diagonale secondaire d’une matrice carrée correspond aux éléments qui vont du coin inférieur gauche au coin supérieur droit :

diagonale secondaire d'une matrice carrée

Propriétés d’une matrice carrée

Les matrices carrées sont très utilisées en algèbre linéaire, c’est pourquoi elles sont si importantes. Voyons donc quelles sont les caractéristiques qui rendent cette classe de matrices si pertinente :

Toute matrice carrée peut être décomposée en une somme d’une matrice symétrique et d’une matrice antisymétrique .

Si deux matrices carrées sont du même ordre, elles peuvent être additionnées ou soustraites l’une de l’autre :

$\begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}$

Deux matrices carrées peuvent être multipliées dans les deux directions possibles. Cependant, le produit des matrices carrées n’est pas commutatif, c’est-à-dire que le résultat de la multiplication changera en fonction du côté par lequel il est multiplié. Remarquez dans l’exemple suivant comment le résultat dépend des positions des matrices :

$\begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}$

$\begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}$

Les matrices carrées sont les seules qui permettent de calculer le déterminant. Par conséquent, un déterminant ne peut être résolu que s’il s’agit d’une matrice carrée. Par exemple, pour trouver le déterminant d’une matrice carrée 3×3, il faut appliquer la règle de Sarrus :

$\displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}$

Rappelez-vous également que si le déterminant de la matrice est différent de 0, cela signifie qu’il s’agit d’une matrice régulière , c’est-à-dire qu’elle est inversible. En revanche, si le déterminant est nul, il s’agit d’une matrice singulière (qui n’a pas d’inverse).

Enfin, les matrices carrées peuvent être diagonalisées . Ainsi un changement de base peut être effectué pour calculer les valeurs propres (ou valeurs propres) et les vecteurs propres (ou vecteurs propres) d’une matrice carrée.

Opérations avec des matrices carrées

Comme nous l’avons vu, le déterminant d’une matrice ne peut être calculé que si la matrice est carrée. De même, il existe également certaines opérations qui ne peuvent être effectuées que si la matrice est de dimension carrée :

trace d’une matrice

La trace d’une matrice est la somme des éléments qui forment la diagonale principale d’une matrice carrée.

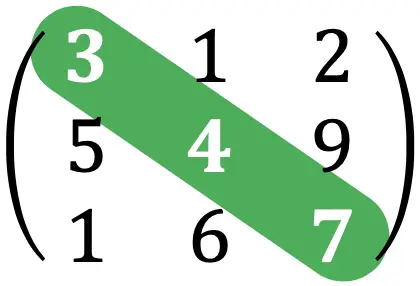
Par exemple, la trace de la matrice de l’exercice ci-dessus serait :

$\text{tr}(A)=3+4+7=\bm{14}$

Types de matrices carrées

Ensuite, vous avez les types de matrices carrées les plus importants qui existent. Cliquez sur le type de matrice pour découvrir ce qu’il a de spécial.