Matrice triangulaire supérieure et inférieure

Sur cette page, vous verrez ce qu’est une matrice triangulaire et les différents types de matrices triangulaires ainsi que des exemples. De plus, vous trouverez comment calculer le déterminant d’une matrice triangulaire et quelles sont les propriétés de cette matrice très intéressante. Enfin, nous expliquons également ce qu’est une matrice de Hessenberg, puisqu’il s’agit d’une matrice apparentée aux matrices triangulaires.

Qu’est-ce qu’une matrice triangulaire ?

Définition de matrice triangulaire :

Une matrice triangulaire est une matrice carrée dans laquelle tous les éléments au-dessus ou au-dessous de la diagonale principale sont nuls (0).

Les matrices triangulaires sont largement utilisées dans les calculs d’algèbre linéaire, car inverser une matrice triangulaire, calculer son déterminant, ou même résoudre des systèmes d’équations linéaires avec ce type de matrices est beaucoup plus facile qu’avec des matrices qui ont des éléments autres que 0 à toutes les positions. .

matrice triangulaire supérieure

Une matrice triangulaire supérieure est une matrice carrée dont les éléments sous la diagonale principale sont nuls (0).

Exemple de matrice triangulaire supérieure :

matrice triangulaire inférieure

Une matrice triangulaire inférieure est une matrice carrée qui a un zéro (0) dans chaque élément qui est au-dessus de la diagonale principale.

Exemple de matrice triangulaire inférieure :

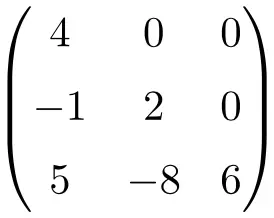
Parfois, ces matrices sont également appelées avec la lettre U, pour la matrice triangulaire supérieure, et avec la lettre L, pour la matrice triangulaire inférieure. Bien que cette nomenclature soit principalement utilisée en anglais, en fait, le U signifie matrice triangulaire supérieure et le L pour matrice triangulaire inférieure .

Exemples de matrices triangulaires

Matrice triangulaire 2 × 2 dimensions

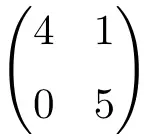
Exemple de matrice triangulaire supérieure 2x2

Matrice triangulaire d’ordre 3×3

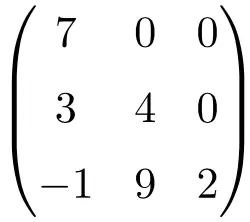
Exemple de matrice triangulaire inférieure 3x3

matrice triangulaire de taille 4×4

Exemple de matrice triangulaire supérieure 4x4

Déterminant d’une matrice triangulaire

Le déterminant d’une matrice triangulaire , qu’elle soit triangulaire supérieure ou inférieure, est le produit des éléments sur la diagonale principale.

Jetez un oeil à l’exercice suivant résolu comment il suffit de calculer la multiplication des éléments de la diagonale principale de la matrice triangulaire pour trouver son déterminant :

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Ce théorème se démontre facilement : il suffit de calculer le déterminant d’une matrice triangulaire par blocs (ou cofacteurs). Cette démonstration est détaillée ci-dessous à l’aide d’une matrice triangulaire générique :

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Par contre, on sait qu’une matrice est inversible si son déterminant est différent de 0. Donc, si aucun élément sur la diagonale principale n’est 0, la matrice triangulaire sera également inversible et, par conséquent, ce sera une matrice régulière matrice.

Propriétés de la matrice triangulaire

Voyons maintenant quelles sont les propriétés des matrices triangulaires :

Le produit de deux matrices triangulaires supérieures est égal à une matrice triangulaire supérieure. Et vice versa : la multiplication de deux matrices triangulaires inférieures donne une autre matrice triangulaire inférieure.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

La transposée d’une matrice triangulaire supérieure est une matrice triangulaire inférieure, et inversement : la transposée d’une matrice triangulaire inférieure est une matrice triangulaire supérieure.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Une matrice triangulaire est inversible si tous ses éléments sur la diagonale principale sont non nuls, c’est-à-dire s’ils sont différents de zéro. Dans un tel cas, l’inverse d’une matrice triangulaire supérieure (inférieure) est également une matrice triangulaire supérieure (inférieure).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

De plus, la diagonale principale de la matrice inversée contiendra toujours les inverses des éléments de la diagonale principale de la matrice triangulaire d’origine.

Toute matrice diagonale est à la fois une matrice triangulaire supérieure et une matrice triangulaire inférieure, par exemple :

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Ainsi une matrice scalaire est aussi une matrice triangulaire supérieure et inférieure. Par exemple la matrice identité :

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Évidemment, la matrice nulle est aussi une matrice triangulaire supérieure et inférieure, car les éléments au-dessus et au-dessous de la diagonale principale sont 0 :

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Les valeurs propres (ou valeurs propres) d’une matrice triangulaire sont les éléments de la diagonale principale.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Une matrice triangulaire supérieure ou inférieure est toujours capable de diagonaliser sur une base de vecteurs propres (ou vecteurs propres).

Toute matrice peut être factorisée en produit d’une matrice triangulaire inférieure et d’une matrice triangulaire supérieure . C’est-à-dire que n’importe quelle matrice peut être transformée en une multiplication de matrice triangulaire. De plus, si la matrice est inversible, cette transformation est unique. Pour factoriser une matrice, la méthode de décomposition LU est souvent utilisée.

Triangulariser une matrice

Il existe plusieurs théorèmes sur les matrices qui peuvent être triangularisées en changeant de base. Cependant, nous allons voir ici comment trianguler une matrice en appliquant des transformations élémentaires sur les lignes , comme dans la méthode de Gauss.

Par exemple:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

Et de cette façon, nous avons déjà triangularisé la matrice d’origine.

Rappelons que les transformations élémentaires autorisées entre lignes dans la méthode gaussienne sont :

Remplacer une ligne par la combinaison linéaire d’autres lignes.
Multipliez ou divisez tous les termes d’une ligne par un nombre autre que 0.
Modifier les lignes de commande.

Matrice de Hessenberg

La définition de la matrice de Hessenberg est la suivante :

La matrice de Hessenberg est une matrice “presque” triangulaire, c’est-à-dire que tous ses éléments sont nuls à partir de la première sous-diagonale (matrice de Hessenberg supérieure) ou de la première superdiagonale (matrice de Hessenberg inférieure).

Je suis sûr que c’est mieux compris avec un exemple de matrice de Hessenberg supérieure et un autre exemple de matrice de Hessenberg inférieure :

Matrice de Hessenberg supérieure

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Matrice de Hessenberg inférieure

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Une matrice qui est à la fois une matrice de Hessenberg supérieure et inférieure est une matrice tridiagonale .

Cette matrice porte le nom de Karl Hessenberg, un éminent ingénieur et mathématicien allemand du XXe siècle.

Enfin, ce type de matrice a la particularité que si elle est multipliée par une matrice triangulaire, le résultat est toujours une matrice de Hessenberg.