Sur cette page, vous trouverez l’explication de la matrice nulle, également appelée matrice nulle. Vous verrez aussi avec des exemples que les valeurs de ses éléments sont indépendantes de la dimension de la matrice, et enfin vous retrouverez toutes les propriétés de ce type de matrice.
Qu’est-ce que la matrice nulle ?
La matrice nulle (ou matrice nulle) est une matrice dont les éléments sont tous égaux à zéro (0).
Par conséquent, par la définition de la matrice nulle, cette matrice peut être de toutes les dimensions possibles tant que tous ses nombres sont nuls. Regardez les exemples suivants :
Exemples de matrices nulles
Exemple de matrice nulle 2 × 2
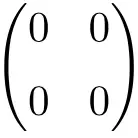
Exemple de matrice nulle 3 × 3
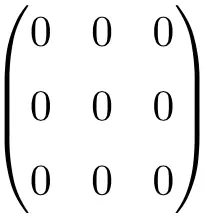
Exemple de matrice nulle 4 × 4
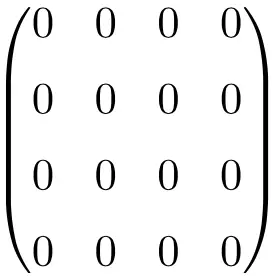
Il vous semble peut-être maintenant que cette matrice très particulière n’a pas d’importance, puisqu’il s’agit simplement d’une matrice pleine de zéros. Cependant, en mathématiques, plus précisément dans le domaine de l’algèbre linéaire, c’est une matrice très utile car elle rend les calculs beaucoup plus faciles.
Propriétés de la matrice nulle
Les matrices nulles (ou nulles) ont les caractéristiques suivantes :
- La matrice nulle est l’élément neutre de l’opération d’addition matricielle, donc :
![]()
- La multiplication matricielle a la propriété multiplicative de zéro, c’est-à-dire que le produit de toute matrice multipliée par la matrice nulle est égal à 0.
![]()
- Si la matrice est carrée, la matrice nulle est à la fois symétrique et antisymétrique .
- La matrice nulle est la seule matrice dont le rang est nul.
- Le déterminant de la matrice nulle est toujours évalué à 0, donc ce type de matrice n’a pas d’inverse (c’est une matrice singulière).
- Évidemment, la matrice nulle est un exemple de matrice nilpotente .