Matrice nilpotente

Sur cette page, vous trouverez une explication de ce qu’est une matrice nilpotente, ainsi que plusieurs exemples afin que vous puissiez la comprendre et n’avoir aucun doute. De plus, vous pourrez voir les structures des matrices nilpotentes et toutes les propriétés de ces types de matrices.

Qu’est-ce qu’une matrice nilpotente ?

La définition de matrice nilpotente est la suivante :

Une matrice nilpotente est une matrice carrée qui élevée à un nombre entier donne la matrice nulle .

$N^k =0$

Où

$N$ est la matrice nilpotente et $k$ l’exposant de la puissance qui donne la matrice nulle.

Cette condition ne signifie pas que la puissance d’une matrice nilpotente donne toujours zéro quel que soit l’exposant, mais plutôt que s’il existe au moins une puissance de la matrice dont le résultat est une matrice pleine de 0, alors la matrice est nilpotente.

D’autre part, l’ indice de nilpotence d’une matrice nilpotente est le plus petit nombre avec lequel la condition de nilpotence est satisfaite. On peut aussi dire que la matrice nilpotente est d’ordre k , où k est son indice de nilpotence.

Exemples de matrices nilpotentes

Pour finir de comprendre le concept de matrice nilpotente, nous allons voir plusieurs exemples de ce type de matrice :

Exemple de matrice nilpotente 2 × 2

La matrice carrée suivante de dimension 2×2 est nilpotente :

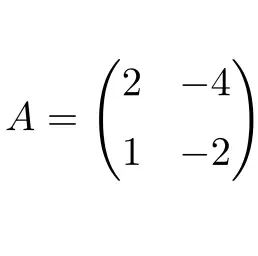
exemple de matrice nilpotente de dimension 2x2

La matrice est nilpotente car en élevant au carré la matrice A on obtient la matrice nulle comme résultat :

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

C’est donc une matrice nilpotente et son indice de nilpotence vaut 2, puisque la matrice nulle est obtenue à la puissance seconde.

Exemple de matrice nilpotente 3×3

La matrice carrée d’ordre 3 suivante est nilpotente :

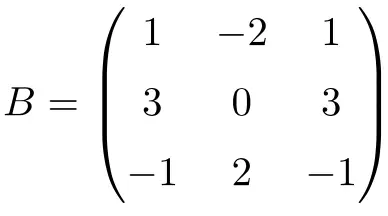
exemple de matrice nilpotente de dimension 3x3

Bien qu’en élevant la matrice à 2, nous n’obtenons pas la matrice nulle :

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Mais lors du calcul du cube de la matrice, nous obtenons une matrice avec tous les éléments égaux à 0 :

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Donc la matrice B est une matrice nilpotente, et comme la matrice nulle est obtenue à la puissance 3, son indice de nilpotence est de 3.

Structure d’une matrice nilpotente 2 × 2

Ci-dessous, vous pouvez voir la structure de toutes les matrices nilpotentes. Sa preuve est un peu fastidieuse, nous vous avons donc directement laissé la formule pour obtenir une matrice nilpotente d’ordre 2 :

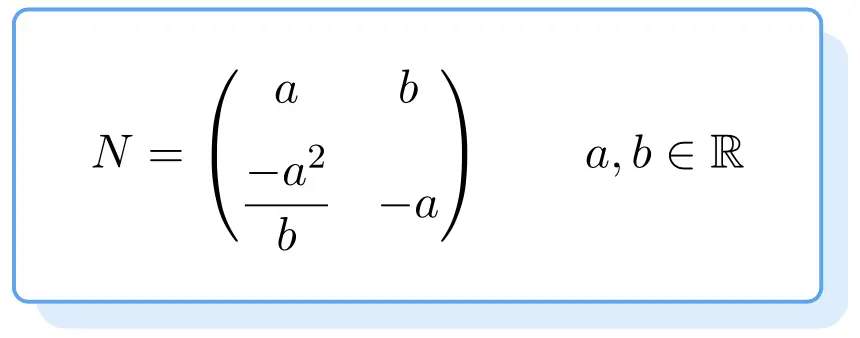
structure et formule d'une matrice nilpotente 2x2

Ainsi, toute matrice qui vérifie la formule ci-dessus sera une matrice nilpotente. Pour cela, les valeurs

$a$ et $b$ ils peuvent être quelconques tant qu’il s’agit de nombres réels.

Propriétés des matrices nilpotentes

Les matrices nilpotentes ont les caractéristiques suivantes :

La trace d’une matrice nilpotente est toujours nulle.

De la même manière, le déterminant de toute matrice nilpotente est toujours égal à 0. Cependant, l’inverse n’est pas vrai, c’est-à-dire que le déterminant d’une matrice est nul n’implique pas que la matrice est nilpotente .

La seule matrice nilpotente diagonalisable est la matrice nulle.

L’indice de nilpotence d’une matrice nilpotente de dimension n×n est toujours égal ou inférieur à n . C’est pourquoi l’indice de nilpotence d’une matrice nilpotente 2 × 2 sera toujours de 2.

Une matrice nilpotente n’est pas inversible.

Toute matrice triangulaire avec des zéros sur la diagonale principale est également une matrice nilpotente.

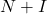Il existe un théorème qui dit que si la matrice $N$ est nilpotente, alors la matrice $N+I$ est inversible, où 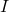$I$ est la matrice d’identité. De plus, sa matrice inverse peut être trouvée avec la formule suivante :

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

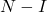De manière équivalente, si $N$ est une matrice nilpotente, alors l’inverse de la matrice peut être calculé $N-I$ avec l’équation suivante :

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Toute matrice singulière, c’est-à-dire non inversible, peut être décomposée en produit de matrices nilpotentes.

Toutes les valeurs propres (ou valeurs propres) d’une matrice nilpotente sont nulles.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

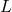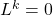Enfin, comme curiosité, il y a aussi le concept de transformation nilpotente, qui définit une application linéaire $L$ d’un espace vectoriel tel que $L^k=0$ .