Matrice scalaire - Mathority

Sur cette page vous trouverez ce qu’est une matrice scalaire et plusieurs exemples de matrices scalaires afin qu’elle soit parfaitement comprise. De plus, vous pourrez voir toutes les propriétés des matrices scalaires et les avantages de faire des opérations avec elles. Enfin, nous expliquons comment calculer le déterminant d’une matrice scalaire et comment inverser ce type de matrice.

Qu’est-ce qu’une matrice scalaire ?

Une matrice scalaire est une matrice diagonale dans laquelle toutes les valeurs de la diagonale principale sont égales.

C’est la définition d’une matrice scalaire, mais je suis sûr que c’est mieux compris avec des exemples : 😉

Exemples de tableaux scalaires

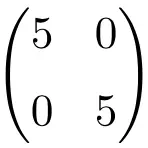
Exemple de matrice scalaire d’ordre 2×2

exemple de matrice scalaire de dimension 2x2

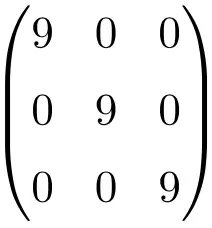
Exemple de matrice scalaire de dimension 3×3

exemple de matrice scalaire de dimension 3x3

Exemple de matrice scalaire de taille 4×4

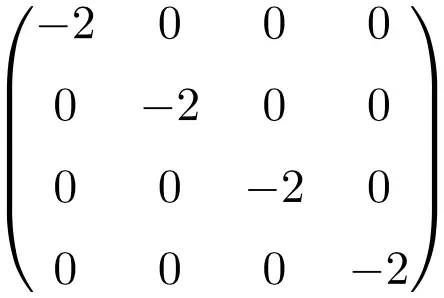
exemple de matrice scalaire de dimension 4x4

Propriétés des matrices scalaires

La matrice scalaire est également une matrice diagonale, vous verrez donc qu’elle hérite de nombreuses caractéristiques de cette classe de matrice :

Toutes les matrices scalaires sont également des matrices symétriques .

Une matrice scalaire est à la fois une matrice triangulaire supérieure et une matrice triangulaire inférieure .

La matrice identité est une matrice scalaire.

Toute matrice scalaire peut être obtenue à partir du produit d’une matrice identité et d’un nombre scalaire.

$4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}$

La matrice nulle est aussi une matrice scalaire.

Les valeurs propres (ou valeurs propres) d’une matrice scalaire sont les éléments de sa diagonale principale. Par conséquent, leurs valeurs propres seront toujours les mêmes et seront répétées autant de fois que la dimension de la matrice.

$\begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8$

L’adjoint d’une matrice scalaire est une autre matrice scalaire. Et de plus, les valeurs de la diagonale principale de la matrice attachée seront toujours celles de la matrice d’origine élevées à l’ordre de la matrice – 1 .

$\displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}$

Opérations avec des matrices scalaires

L’une des raisons pour lesquelles les matrices scalaires sont si largement utilisées en algèbre linéaire est la facilité avec laquelle elles vous permettent d’effectuer des calculs. C’est pourquoi ils sont si importants en mathématiques.

Voyons donc pourquoi il est si facile de faire des calculs avec ce type de matrices carrées :

Addition et soustraction de matrices scalaires

L’addition (et la soustraction) de deux matrices scalaires est très simple : il suffit d’additionner (ou de soustraire) les nombres sur les diagonales principales. Par exemple:

$\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}$

Multiplication de matrice scalaire

De manière similaire à l’addition et à la soustraction, pour résoudre une multiplication ou un produit matriciel entre deux matrices scalaires, il suffit de multiplier les éléments des diagonales entre eux. Par exemple:

$\displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}$

Puissance des matrices scalaires

Le calcul de la puissance d’une matrice scalaire est également très simple : il faut élever chaque élément de la diagonale à l’exposant. Par exemple:

*** QuickLaTeX cannot compile formula:
\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^4 & 0 & 0 \\[1.1ex] 0 & 2^

*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \right. inserted.
leading text: \end{document}

& 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 & 16 \end{pmatrix} $<div class="adsb30" style=" margin:px; text-align:"></div><h2 class="wp-block-heading"> Déterminant d'une matrice scalaire</h2> Calculer le <strong>déterminant d'une matrice scalaire</strong> revient à résoudre le déterminant d'une matrice diagonale : le résultat est le produit des éléments sur la diagonale principale.$ \displaystyle \text{det}(A)= \prod_{i =1}^n a_i $Regardez l'exercice résolu suivant dans lequel on trouve le déterminant d'une matrice scalaire en multipliant les éléments de sa diagonale principale :$ \displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm{343} $En fait, puisque tous les éléments de la diagonale principale d'une matrice scalaire sont toujours égaux, pour trouver le résultat du déterminant, il suffit d'augmenter le numéro de la diagonale principale du nombre de fois qu'elle est répétée. Par conséquent, l'exercice précédent peut également être résolu de la manière suivante :$ \displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343} $Démontrer ce théorème est très simple : il suffit de calculer le déterminant d'une matrice scalaire par blocs (ou cofacteurs). 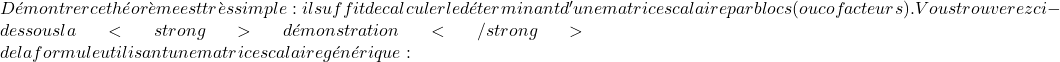Vous trouverez ci-dessous la <strong>démonstration</strong> de la formule utilisant une matrice scalaire générique :$ \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} – 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) – 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{aligned} $Dans ce cas ça donne$ a^3 $car la matrice est d'ordre 3, mais il faut toujours l'élever à l'ordre de la matrice. <div class="adsb30" style=" margin:12px; text-align:center"><div id="ezoic-pub-ad-placeholder-118"></div></div><h2 class="wp-block-heading"> Inverser une matrice scalaire</h2> Une matrice scalaire <strong>est inversible si, et seulement si, tous les éléments de la diagonale principale sont différents de 0</strong> . Dans ce cas on dit que la matrice scalaire est une matrice régulière. De plus, l'inverse d'une matrice scalaire sera toujours une autre matrice scalaire avec les <strong>inverses</strong> de la diagonale principale :$ \displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{1}{9} \end{pmatrix} $D'autre part, de la caractéristique précédente, on peut déduire que le déterminant d'une matrice scalaire inversée est le résultat de la multiplication des inverses de la diagonale principale :$ \displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = 0,125 $