Sur cette page, vous verrez ce qu’est une matrice diagonale et des exemples de matrices diagonales. De plus, vous découvrirez comment opérer avec ce type de matrices, comment calculer facilement leurs déterminants et comment les inverser. Il existe également des propriétés et des applications des matrices diagonales. Et, enfin, il y a les explications d’une matrice bidiagonale et d’une matrice tridiagonale.
Qu’est-ce qu’une matrice diagonale ?
Une matrice diagonale est une matrice carrée dans laquelle tous les éléments qui ne sont pas sur la diagonale principale sont nuls (0). Les éléments de la diagonale principale peuvent être nuls ou non.
Une fois que nous connaissons la définition exacte d’une matrice diagonale, nous allons voir des exemples de matrices diagonales :
Exemples de matrices diagonales
Exemple de matrice diagonale de dimension 2 × 2
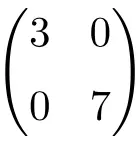
Exemple de matrice diagonale d’ordre 3×3

Exemple de matrice diagonale de taille 4×4
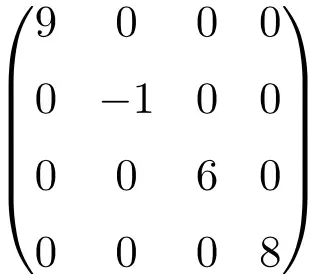
Ces types de matrices s’écrivent généralement en indiquant les éléments de la diagonale :
![Rendered by QuickLaTeX.com diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14216c3a6fd6e7bfd4c9d78ac2a4765c_l3.png)
Opérations avec des matrices diagonales
L’une des raisons pour lesquelles les matrices diagonales sont si importantes pour l’algèbre linéaire est la facilité avec laquelle elles vous permettent d’effectuer des calculs. C’est pourquoi ils sont si utilisés en mathématiques.
Ajouter et soustraire des matrices diagonales
L’addition (et la soustraction) de deux matrices diagonales est très simple : il suffit d’additionner (ou de soustraire) les nombres sur les diagonales.
![]()
Par exemple:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e659649fca7fe55f33c0f3452e8c46f2_l3.png)
Multiplication matricielle diagonale
Pour résoudre une multiplication ou un produit matriciel de deux matrices diagonales, il suffit de multiplier les éléments des diagonales ensemble.
![]()
Par exemple:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0bcb4a59778cc41eed67dce0bc384682_l3.png)
Puissance des matrices diagonales
Pour calculer la puissance d’une matrice diagonale, nous devons élever chaque élément de la diagonale à l’exposant :
![]()
![]()
Par exemple:
![Rendered by QuickLaTeX.com \displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d27337283f4b6029bff166fb8e3458d_l3.png)
Déterminant d’une matrice diagonale
Le déterminant d’une matrice diagonale est le produit des éléments sur la diagonale principale.
![]()
![]()
Regardez l’exercice résolu suivant dans lequel on trouve le déterminant d’une matrice diagonale simplement en multipliant les éléments de sa diagonale principale :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30](https://mathority.org/wp-content/ql-cache/quicklatex.com-f34514c6e1559b8ebb296ee6c51a33d6_l3.png)
Ce théorème est facile à prouver : il suffit de calculer le déterminant d’une matrice diagonale par blocs (ou cofacteurs). Cette démonstration est détaillée ci-dessous à l’aide d’une matrice diagonale générique :
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b8718172b4b70d1ccacb01ea7ed5dd4_l3.png)
Inverser une matrice diagonale
Une matrice diagonale est inversible si et seulement si tous les éléments de la diagonale principale sont différents de 0 . Dans ce cas on dit que la matrice diagonale est une matrice régulière.
De plus, l’inverse d’une matrice diagonale sera toujours une autre matrice diagonale avec les inverses de la diagonale principale :
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91beaaca82477a0c882b42da4eb7481_l3.png)
De la caractéristique précédente, on peut déduire que le déterminant de l’inverse d’une matrice diagonale est le produit des inverses de la diagonale principale :
![Rendered by QuickLaTeX.com \displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0571390802f955fac935aeb9cf4ab92f_l3.png)
![]()
Propriétés des matrices diagonales
- Toute matrice diagonale est aussi une matrice symétrique .
- Une matrice diagonale est une matrice à la fois triangulaire supérieure et inférieure .
- La matrice identité est une matrice diagonale :
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png)
- De même, la matrice nulle est également une matrice diagonale, car tous ses éléments qui ne sont pas sur la diagonale sont des zéros. Bien que les nombres sur la diagonale soient 0.
![Rendered by QuickLaTeX.com \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png)
- Les valeurs propres (ou valeurs propres) d’une matrice diagonale sont les éléments de sa diagonale principale.
![Rendered by QuickLaTeX.com \begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7](https://mathority.org/wp-content/ql-cache/quicklatex.com-1dea3de2ae28d46194ead012bc001cf0_l3.png)
- Une matrice carrée est diagonale si et seulement si elle est triangulaire et normale .
- L’ adjoint d’une matrice diagonale est une autre matrice diagonale.
Applications de matrice diagonale
Comme nous l’avons vu, résoudre des calculs avec des matrices diagonales est très simple, car de nombreux zéros sont impliqués dans les opérations. Pour cette raison, ils sont très utiles dans le domaine des mathématiques et sont largement utilisés.
Pour cette même raison, tant d’études ont été faites sur la façon de diagonaliser une matrice et, en fait, une méthode de diagonalisation des matrices a même été élaborée (en utilisant le polynôme caractéristique).
Par conséquent, les matrices diagonalisables sont également tout à fait pertinentes. Comme le théorème de décomposition spectrale, qui établit les conditions pour lesquelles une matrice peut être diagonalisée et quand elle ne l’est pas.
matrice bidiagonale
Une matrice bidiagonale est une matrice carrée dans laquelle tous les éléments qui ne sont pas sur la diagonale principale ou sur la diagonale supérieure ou inférieure sont 0.
Par exemple:
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d9acdfc09d0167548ef3f6f5b58d9276_l3.png)
matrice bidiagonale supérieure
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2b53f238add73431696006f4b05a2d8_l3.png)
matrice bidiagonale inférieure
Lorsque la diagonale principale et la première superdiagonale sont occupées, on parle de matrice bidiagonale supérieure. En revanche, lorsque la diagonale principale et la première sous-diagonale sont occupées, on parle de matrice bidiagonale inférieure.
matrice tridiagonale
Une matrice tridiagonale est une matrice carrée dont les seuls éléments non nuls sont ceux de la diagonale principale et des diagonales adjacentes au-dessus et au-dessous.
Par exemple:
![Rendered by QuickLaTeX.com \begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a8fbe0404c447268a89ff954e3b23d5_l3.png)
Ainsi, toutes les matrices diagonales, bidiagonales et tridiagonales sont des exemples de matrices de bande . Parce qu’une matrice de bande est cette matrice qui a tous ses éléments non nuls autour de la diagonale principale.