Sur cette page vous trouverez tout sur la tangente hyperbolique : quelle est sa formule, sa représentation graphique, toutes ses caractéristiques,…
Formule de tangente hyperbolique
La fonction tangente hyperbolique est l’une des principales fonctions hyperboliques et est représentée par le symbole tanh(x) . Mathématiquement, la tangente hyperbolique est égale au sinus hyperbolique divisé par le cosinus hyperbolique.
![]()
À partir de la formule du sinus hyperbolique et de la formule du cosinus hyperbolique, nous pouvons arriver à l’expression suivante :
![]()
Par conséquent, la fonction tangente hyperbolique est liée à la fonction exponentielle. Dans le lien suivant, vous pouvez voir toutes les caractéristiques de ces types de fonctions :
➤ Voir : caractéristiques des fonctions exponentielles
Représentation graphique de la tangente hyperbolique
A partir de sa formule, on peut représenter graphiquement la fonction tangente hyperbolique :
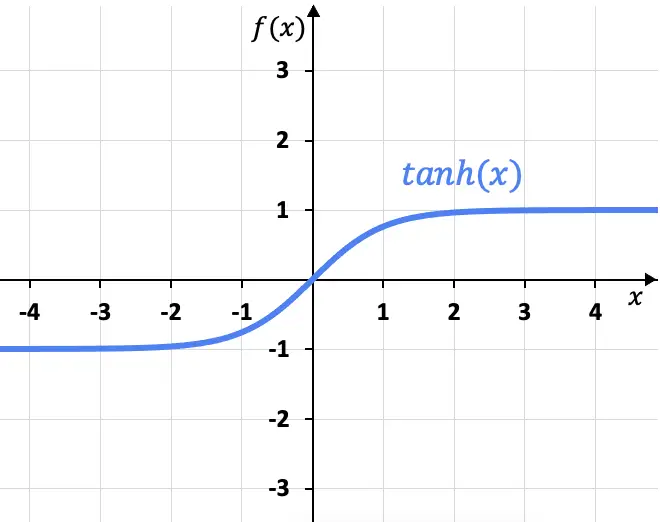
Comme vous pouvez le voir sur le graphique, la fonction tangente hyperbolique a deux asymptotes horizontales à x=+1 et x=-1, puisque la limite de la fonction lorsque x tend vers plus l’infini donne x=+1, et la limite à moins l’infini donne x=-1.
Par contre, le graphe de la tangente hyperbolique n’a rien à voir avec le graphe de la tangente (fonction trigonométrique), qui est une fonction périodique. Vous pouvez voir la représentation graphique de la tangente et comment elle diffère de la tangente hyperbolique dans le lien suivant :
➤ Voir : représentation graphique de la fonction tangente
Caractéristiques de la tangente hyperbolique
La fonction tangente hyperbolique a les propriétés suivantes :
- Le domaine de la fonction tangente hyperbolique est tous les nombres réels.
![]()
- En revanche, le chemin ou la plage de la fonction tangente hyperbolique est limité aux valeurs comprises entre -1 et +1 (non inclus).
![]()
- La tangente hyperbolique est une fonction continue, bijective et impaire (symétrique par rapport à l’origine des coordonnées).
![]()
- La fonction coupe l’axe X et l’axe Y à l’origine des coordonnées.
![]()
- Les limites à plus/moins l’infini de la fonction tangente hyperbolique donnent +1/-1. Par conséquent, la fonction a une asymptote horizontale en x=+1 et une autre asymptote horizontale en x=-1.
![]()
![]()
- La tangente hyperbolique est strictement croissante sur tout son domaine, elle n’a donc pas d’extrema relatif (ni maximum ni minimum).
- Cependant, la fonction passe de convexe à concave au point x = 0, donc x = 0 est un point d’inflexion de la fonction.
- L’inverse de la fonction tangente hyperbolique est appelé l’argument tangente hyperbolique (ou arctangente hyperbolique) et sa formule est la suivante :
![]()
- La dérivée de la fonction tangente hyperbolique est 1 divisé par le carré du cosinus hyperbolique :
![]()
- L’intégrale de la fonction tangente hyperbolique est le logarithme naturel du cosinus hyperbolique :
![]()
- La tangente hyperbolique de la somme de deux nombres différents peut être calculée en appliquant l’équation suivante :
![]()
- Le polynôme de Taylor ou la série de la tangente hyperbolique a le rayon de convergence
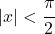 et correspond à l’expression suivante :
et correspond à l’expression suivante :
![]()
Où
![]() est le nombre de Bernoulli .
est le nombre de Bernoulli .