Fonction exponentielle

Sur cette page vous découvrirez ce que sont les fonctions exponentielles et aussi comment représenter une fonction exponentielle sur un graphique. De plus, vous verrez toutes ses caractéristiques et plusieurs exemples pour parfaitement le comprendre. Enfin, vous pourrez vous entraîner avec des exercices et des problèmes résolus étape par étape sur des fonctions exponentielles.

Qu’est-ce qu’une fonction exponentielle ?

La définition d’une fonction exponentielle est la suivante :

Exemples de fonctions exponentielles

Les fonctions suivantes sont des exemples de fonctions exponentielles :

Caractéristiques des fonctions exponentielles

Les fonctions exponentielles ont les propriétés suivantes :

• Le domaine d’une fonction exponentielle est constitué de nombres réels, ou en d’autres termes, une fonction exponentielle existe pour toute valeur de x .

• Cependant, la fonction ne prend que des valeurs positives, donc la plage d’une fonction exponentielle est constituée de nombres réels positifs.

• Chaque fonction exponentielle est à la fois une fonction continue et injective.

• Si la fonction n’est pas traduite, toute fonction exponentielle passe par le point (0,1). Parce que la fonction évaluée à zéro donne toujours un.

• De même, la valeur d’une fonction exponentielle à x=1 est égale à la base.

• Si la base d’alimentation 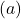est supérieur à 1, la fonction exponentielle est croissante. En revanche, si le coefficient est dans l’intervalle entre 0 et 1, la fonction exponentielle est décroissante.

• En général, l’axe des x est une asymptote horizontale d’une fonction exponentielle.

• L’inverse de la fonction exponentielle est la fonction logarithmique. Par conséquent, les graphiques d’une fonction exponentielle et d’une fonction logarithmique sont symétriques par rapport à la droite y=x si les deux ont la même base.

Comment tracer graphiquement une fonction exponentielle

Les fonctions exponentielles sont très simples à représenter. Voyons donc comment représenter graphiquement une fonction exponentielle sur un graphique à l’aide d’un exemple.

• Représentez la fonction exponentielle suivante sur un graphique :

Dans les fonctions exponentielles, il n’est pas nécessaire de calculer le domaine, car ce seront toujours tous des nombres réels :

Il suffit donc de faire le tableau des valeurs. Comme ces types de fonctions changent beaucoup d’un point à un autre, nous calculerons 5 points. Mais plus nous calculons de points, plus la représentation de la fonction sera précise.

Nous vous recommandons d’utiliser une calculatrice pour trouver les points dans le tableau des valeurs, car ils sont compliqués à calculer à la main.

Maintenant, nous représentons les points sur un graphique :

Et enfin, nous joignons les points et allongeons la fonction :

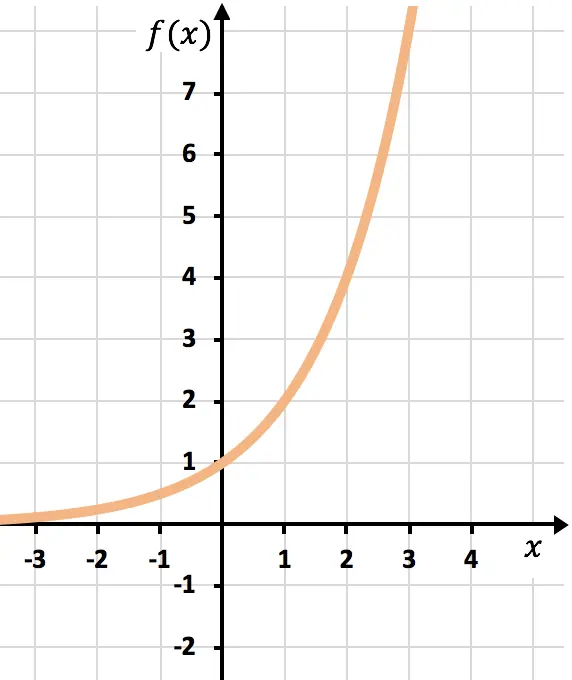
Notez que la fonction de droite continue de croître jusqu’à l’infini.

En revanche, la fonction de gauche diminue mais n’atteint jamais 0. Même si elle s’en rapproche beaucoup, elle ne le touche jamais. Cela signifie que la droite y=0 (l’axe des abscisses) est une asymptote horizontale.

Exercices résolus sur les fonctions exponentielles

Exercice 1

Représentez graphiquement la fonction exponentielle suivante :

C’est une fonction exponentielle, donc pour la représenter il faut créer un tableau de valeurs donnant des valeurs à la variable x :

Une fois que nous avons le tableau des valeurs, nous représentons les points obtenus sur le graphique et traçons la fonction :

Notez que la fonction de droite continue de croître jusqu’à l’infini. En revanche, à gauche, la fonction diminue mais ne dépasse jamais 1. En effet, la fonction a une asymptote horizontale sur la droite y=1.

Dans ce cas, l’asymptote horizontale est à y=1 au lieu de l’axe OX car une translation verticale d’une unité vers le haut a été effectuée vers la fonction.

Exercice 2

Représentez la fonction exponentielle suivante sur un graphique :

C’est une fonction exponentielle, donc pour la représenter graphiquement il faut construire un tableau de valeurs donnant des valeurs à la variable x :

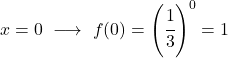
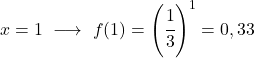
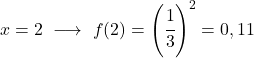
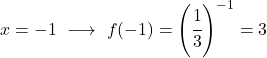
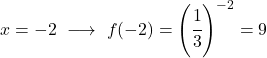
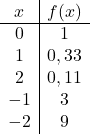
Une fois que nous avons le tableau des valeurs, nous représentons les points calculés sur le graphique et dessinons la fonction :

Notez que la fonction de gauche continue de croître jusqu’à l’infini. En revanche, à droite, la fonction diminue mais ne dépasse jamais 0. En effet, la fonction a une asymptote horizontale en y=0 (l’axe X).

Exercice 3

Représentez la fonction exponentielle suivante sur un graphique :

Il s’agit d’une fonction exponentielle, donc pour la dessiner il faut créer un tableau de valeurs évaluant la fonction en plusieurs points :

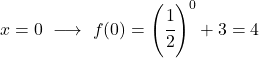
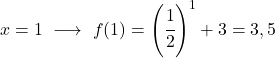
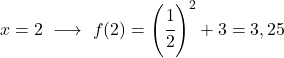
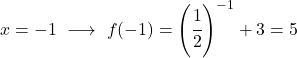
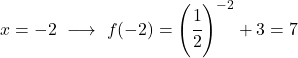
Enfin, nous représentons les points obtenus sur le graphique et traçons la fonction :

Notez que la fonction de gauche croît de manière illimitée jusqu’à l’infini. En revanche, à droite, la fonction diminue mais ne dépasse jamais 3. En effet, la fonction a une asymptote horizontale en y=3.

Dans ce cas, l’asymptote horizontale est à y=3 au lieu de l’axe X car la fonction a été déplacée verticalement de trois unités vers le haut.

Exercice 4

Résolvez le problème suivant concernant les fonctions exponentielles.

• Déterminer la valeur de de sorte que la fonction exponentielle suivante passe par le point (2,8).

La fonction doit passer par le point (2,8), on peut donc substituer les valeurs de x et f(x) du point dans la fonction pour trouver la valeur de la constante k :

Et maintenant, nous résolvons l’équation résultante :

Exercice 5

Résolvez le problème suivant concernant les fonctions exponentielles.

Une population de termites se reproduit selon la fonction suivante :

Où

est le nombre de termites et le temps s’est écoulé en mois.

Combien y aura-t-il de termites après 1 an ?

Pour calculer le nombre de termites qu’il y aura dans une année, il suffit de substituer le temps écoulé (1 an) dans la fonction. Mais comme la fonction t est les mois écoulés et non les années, il faut mettre t =12 puisque dans une année il y a 12 mois :

On résout avec la calculatrice :

Ainsi, après un an, il y aura 1 594 323 termites.