Fonction cosinus hyperbolique

Vous trouverez ici tout sur la fonction cosinus hyperbolique : quelle est sa formule, sa représentation graphique, ses caractéristiques, les relations mathématiques avec les autres fonctions,…

Formule cosinus hyperbolique

La fonction cosinus hyperbolique est l’une des principales fonctions hyperboliques et est représentée par le symbole cosh(x) . Le cosinus hyperbolique est égal à la somme de e ^x plus e ^-x divisée par 2.

Par conséquent, la formule du cosinus hyperbolique est la suivante :

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Ainsi, le cosinus hyperbolique est mathématiquement lié à la fonction exponentielle. Dans le lien suivant, vous pouvez voir les propriétés de ce type de fonction :

➤ Voir : propriétés de la fonction exponentielle

Représentation graphique du cosinus hyperbolique

La représentation graphique de la fonction cosinus hyperbolique se présente sous la forme d’une fonction quadratique (ou parabole) :

➤ Voir : Représentation graphique d’une fonction quadratique .

Dans ce graphique, nous pouvons clairement voir que le cosinus hyperbolique est une fonction paire, car elle est symétrique par rapport à l’axe des ordonnées.

Par contre, le graphique du cosinus hyperbolique est très différent de celui du cosinus (fonction trigonométrique), qui est une fonction périodique. Vous pouvez voir la représentation graphique du cosinus et toutes les différences avec le cosinus hyperbolique dans le lien suivant :

➤ Voir : représentation graphique de la fonction cosinus

Caractéristiques du cosinus hyperbolique

Le cosinus hyperbolique respecte les propriétés suivantes :

Le domaine de la fonction cosinus hyperbolique est tous les nombres réels :

$\text{Dom } f = \mathbb{R}$

Au lieu de cela, la plage (ou la plage) de la fonction cosinus hyperbolique est 1 et tous les nombres supérieurs à 1 :

$\text{Im } f= [1,+\infty)$

Le cosinus hyperbolique est une fonction continue et paire.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

La fonction coupe l’axe Y au point x=0.

$(0,1)$

Par contre, la fonction n’a pas de point d’intersection avec l’axe X.

Les deux limites à l’infini (positive et négative) de la fonction cosinus hyperbolique donnent plus l’infini.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

Le cosinus hyperbolique diminue jusqu’à x = 0 et à partir de ce point, il augmente indéfiniment, de sorte que la fonction a un minimum à x = 0.

$(0,1)$

La fonction est convexe dans tout son domaine, elle n’a donc pas de point d’inflexion.

La dérivée de la fonction cosinus hyperbolique est le sinus hyperbolique :

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

L’intégrale de la fonction cosinus hyperbolique est le sinus hyperbolique :

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Le polynôme de Taylor (ou série de Maclaurin) de la fonction cosinus hyperbolique est le suivant :

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

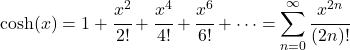
La transformée de Laplace de la fonction cosinus hyperbolique est la suivante :

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Relations mathématiques du cosinus hyperbolique

Ensuite, nous allons voir comment le cosinus hyperbolique peut être calculé à partir d’autres fonctions hyperboliques, puisqu’elles sont toutes liées mathématiquement.

L’équation fondamentale relie le cosinus hyperbolique au sinus hyperbolique :

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Voir : sinus hyperbolique

Les trois principales fonctions hyperboliques (sinus, cosinus et tangente hyperboliques) peuvent être liées par l’équation suivante :

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

D’autre part, le cosinus hyperbolique de l’addition (ou de la soustraction) de deux nombres différents peut être déterminé par les formules suivantes :

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

Le cosinus hyperbolique de deux fois un nombre est égal à la somme des carrés du cosinus hyperbolique et du sinus hyperbolique de ce nombre :

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

L’addition ou la soustraction de deux cosinus hyperboliques peut être calculée en appliquant les formules suivantes :

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Enfin, le carré du cosinus hyperbolique peut être calculé avec la formule suivante :

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Formule cosinus hyperbolique

Représentation graphique du cosinus hyperbolique

Caractéristiques du cosinus hyperbolique

Relations mathématiques du cosinus hyperbolique

Leave a Comment Cancel Reply