Fonction sinus hyperbolique

Dans cet article vous trouverez tout sur le sinus hyperbolique : quelle est sa formule, sa représentation graphique, toutes ses caractéristiques, les relations avec les autres fonctions,…

Formule sinus hyperbolique

La fonction sinus hyperbolique est l’une des principales fonctions hyperboliques et est représentée par le symbole sinh(x) ou sinh(x) . Le sinus hyperbolique est égal à e ^x moins e ^-x divisé par 2.

La formule du sinus hyperbolique est donc la suivante :

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

Ainsi, le sinus hyperbolique est lié à la fonction exponentielle.

➤ Voir : caractéristiques de la fonction exponentielle

Représentation graphique du sinus hyperbolique

En utilisant la formule que nous avons vue dans la section précédente, nous pouvons faire un tableau des valeurs du sinus hyperbolique et représenter graphiquement la fonction :

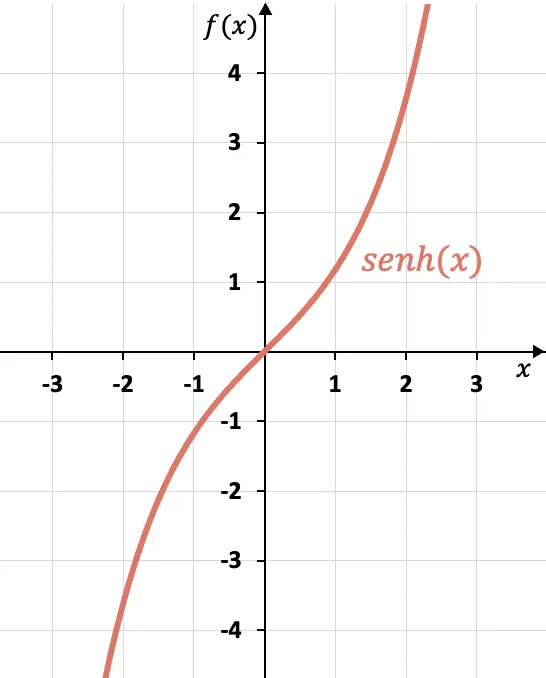
Dans ce graphique, on peut voir que le sinus hyperbolique est une fonction impaire , car les x opposés ont des images opposées, ou en d’autres termes, le graphique du sinus hyperbolique est symétrique par rapport à l’origine des coordonnées (0,0).

Comme vous pouvez le voir, le graphique du sinus hyperbolique est très différent de celui du sinus, qui est une fonction périodique. Vous pouvez voir la représentation graphique du sinus et toutes les différences avec le sinus hyperbolique dans le lien suivant :

➤ Voir : Représentation graphique de la fonction sinus

Caractéristiques du sinus hyperbolique

Le sinus hyperbolique a les propriétés suivantes :

Le domaine de la fonction sinus hyperbolique est tous les nombres réels :

$\text{Dom } f = \mathbb{R}$

La plage ou la plage de la fonction sinus hyperbolique sont également tous des nombres réels.

$\text{Im } f= \mathbb{R}$

Le sinus hyperbolique est une fonction continue et impaire.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Intercepte l’axe X et l’axe Y au même point d’intersection, l’origine des coordonnées :

$(0,0)$

La limite de la fonction sinus hyperbolique lorsque x tend vers plus/moins l’infini est égale à plus/moins l’infini :

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

Le sinus hyperbolique est strictement croissant dans tout le domaine, il n’a donc ni maxima ni minima.

Cependant, il change sa courbure au point x = 0, c’est donc un point d’inflexion de la fonction. Pour les valeurs inférieures à x=0 c’est une fonction concave, par contre pour les valeurs supérieures à x=0 c’est une fonction convexe.

La dérivée de la fonction sinus hyperbolique est le cosinus hyperbolique :

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

De même, l’intégrale de la fonction sinus hyperbolique est le cosinus hyperbolique :

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

La série de Taylor de la fonction sinus hyperbolique est équivalente à l’expression suivante :

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

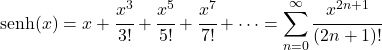
La transformée de Laplace de la fonction sinus hyperbolique est la suivante :

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Relations mathématiques du sinus hyperbolique

Le sinus hyperbolique est lié aux autres fonctions hyperboliques par les équations suivantes :

L’équation fondamentale relie le sinus hyperbolique au cosinus hyperbolique :

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Par conséquent, les fonctions hyperboliques sinus et cosinus sont liées par l’équation de l’hyperbole, qui est x ² -y ² =1. Contrairement aux fonctions trigonométriques sinus et cosinus qui sont liées par l’équation du cercle (x ² +y ² =1).

Les fonctions hyperboliques du sinus, du cosinus et de la tangente peuvent être liées par l’équation suivante :

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

D’autre part, le sinus hyperbolique de l’addition ou de la soustraction de deux nombres différents peut être calculé avec les formules suivantes :

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

Le sinus hyperbolique de deux fois un nombre peut être déterminé en appliquant la relation mathématique suivante :

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

La somme ou la soustraction de deux sinus hyperboliques peut être trouvée à l’aide des formules suivantes :

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Enfin, le carré du sinus hyperbolique peut être calculé en appliquant la formule suivante :

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Formule sinus hyperbolique

Représentation graphique du sinus hyperbolique

Caractéristiques du sinus hyperbolique

Relations mathématiques du sinus hyperbolique

Leave a Comment Cancel Reply