Fonction tangente - Mathority

Sur cette page, vous trouverez tout sur la fonction tangente : qu’est-ce que c’est, quelle est sa formule, comment la représenter dans un graphique, les caractéristiques de la fonction, sa période, etc. De plus, vous pourrez voir des exemples de fonctions tangentes pour bien comprendre le concept. Il explique même le théorème de tangente et les relations que la fonction tangente entretient avec les autres rapports trigonométriques.

Formule de la fonction tangente

La fonction tangente d’un angle α est une fonction trigonométrique dont la formule est définie comme le rapport entre la branche opposée et la branche contiguë (ou adjacente) d’un triangle rectangle (triangle avec un angle droit).

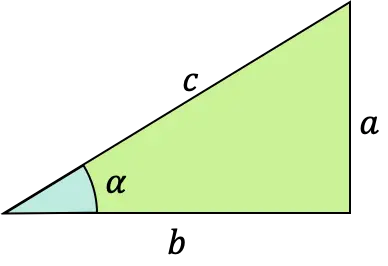
la tangente est une fonction trigonométrique

Ce type de fonction mathématique est également appelé fonction tangentoïde, tangénoïde ou tangentielle. Et il peut être exprimé avec l’abréviation “tg” ou encore “tan”.

La fonction tangente est l’un des trois rapports trigonométriques les plus connus, avec le sinus et le cosinus d’un angle.

Valeurs caractéristiques de la fonction tangente

Il existe des angles déterminés qui se répètent fréquemment et, par conséquent, il est commode de connaître la valeur de la fonction tangente à ces angles :

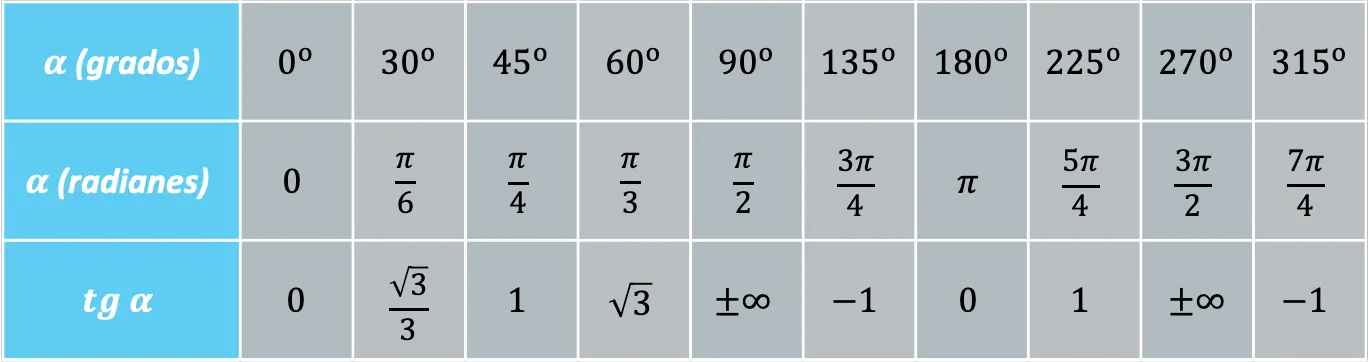
D’autre part, la fonction tangente peut être liée aux fonctions sinus et cosinus par l’identité fondamentale trigonométrique suivante :

$\text{tg } \alpha = \cfrac{\text{sen }\alpha}{\text{cos }\alpha}$

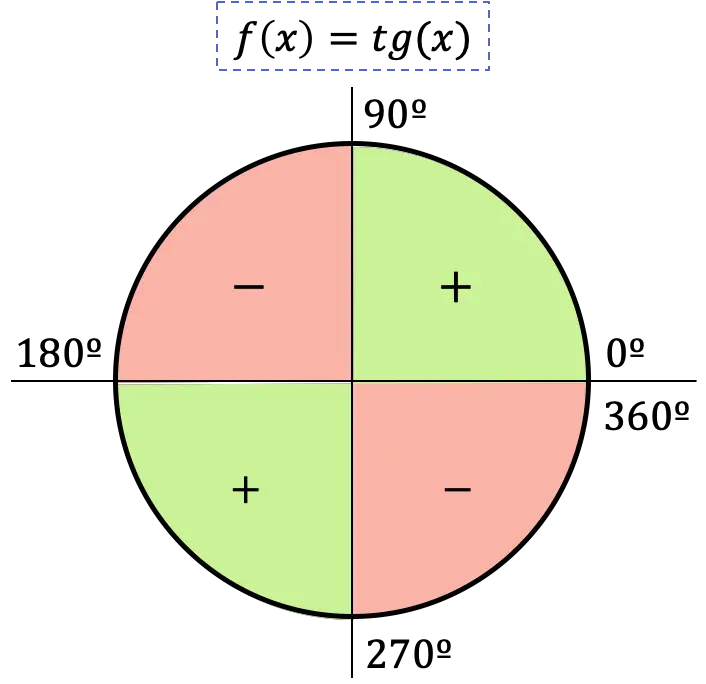
Ainsi, le signe de la fonction tangente dépend du quadrant dans lequel se trouve l’angle :

Si l’angle appartient au premier quadrant, sa tangente sera positive, puisque dans ce quadrant le sinus et le cosinus sont également positifs.
Si l’angle tombe dans le deuxième quadrant, sa tangente sera négative, car dans ce quadrant le sinus est positif mais le cosinus est négatif.
Si l’angle est dans le troisième quadrant, sa tangente sera positive, car dans ce quadrant, le sinus et le cosinus sont négatifs.
Si l’angle est dans le quatrième quadrant, sa tangente sera négative, puisque dans ce quadrant le sinus est négatif et à la place le cosinus est positif.

Représentation graphique de la fonction tangente

Avec le tableau des valeurs que nous avons vu dans la section précédente, nous pouvons représenter graphiquement la fonction tangente. Et en représentant graphiquement la fonction tangente, on obtient :

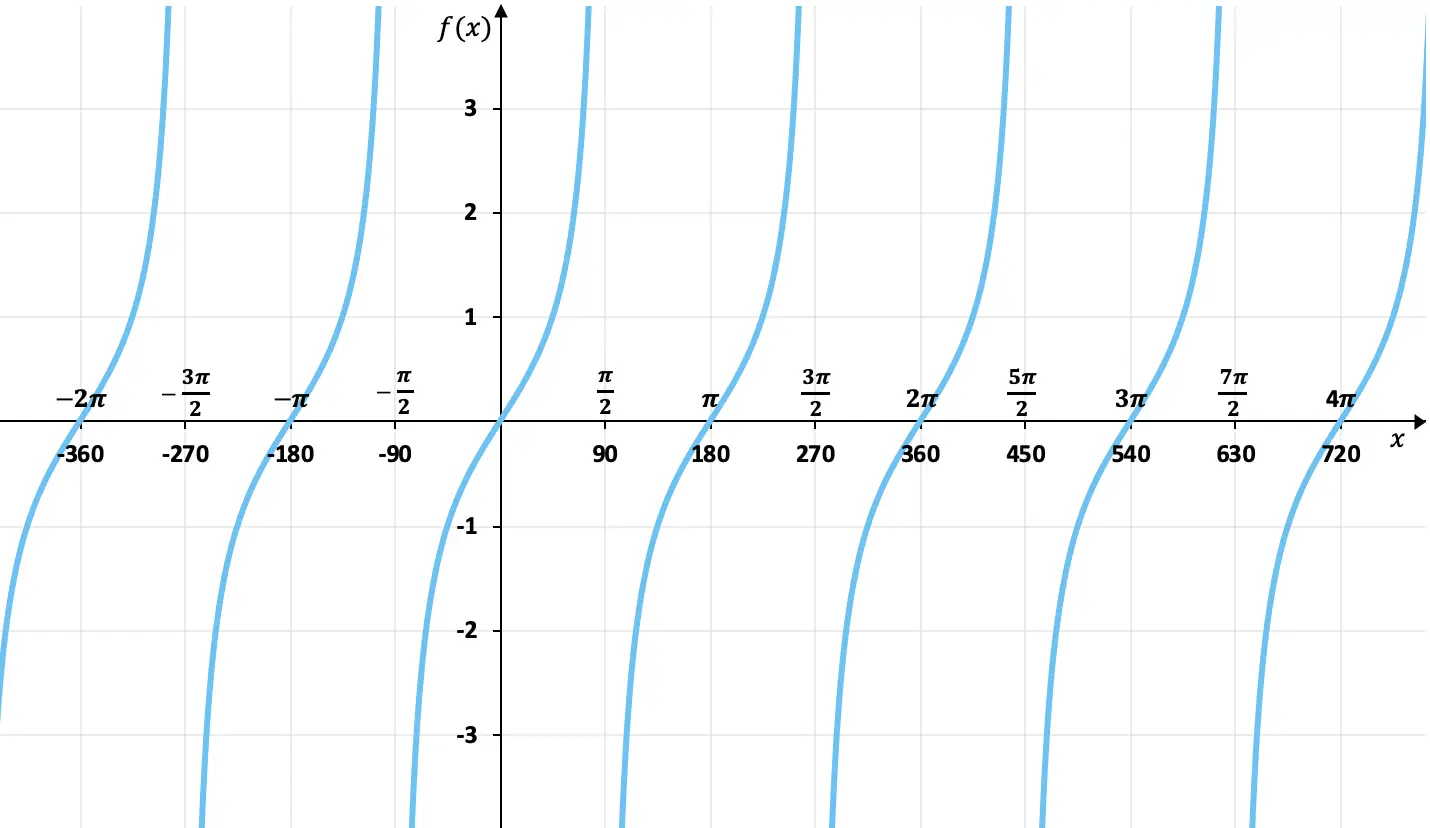
Comme vous pouvez le voir sur le graphique, les valeurs des images de la fonction tangente ne sont pas bornées, contrairement aux fonctions sinus et cosinus. De plus, les valeurs sont répétées tous les 180 degrés (π radians), c’est donc une fonction périodique dont la période est de 180º.

D’autre part, dans ce graphique, on peut voir que la fonction tangente est impaire , car ses éléments opposés ont des images opposées, ou en d’autres termes, elle est symétrique par rapport à l’origine (0,0). Par exemple, la tangente de 45° vaut 1 et celle de -45° vaut -1.

Enfin, on peut également voir que la fonction tangente a des asymptotes verticales . Par exemple, il s’approche très près de la ligne x=90º mais ne la touche jamais, et la même chose se produit tous les 180 degrés. Cela signifie que la limite de la fonction en ces points tend vers l’infini.

Propriétés de la fonction tangente

La fonction tangente a les caractéristiques suivantes :

Le domaine de la fonction tangente est tous les nombres réels sauf les points où il y a une asymptote verticale :

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{(2k+1)\cdot \frac{\pi}{2} \right\} \qquad k \in \mathbb{Z}$

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{\ldots \ , \ -\frac{\pi}{2} \ , \ \frac{\pi}{2} \ , \ \frac{3\pi}{2} \ , \ \ldots \right\}$

La plage ou la plage de la fonction tangente sont tous des nombres réels.

$\text{Im } f= \mathbb{R}$

C’est une fonction continue et impaire de périodicité π.

$\displaystyle \text{tg}(-x) =- \text{tg }x$

Ce type de fonction trigonométrique a un seul point d’intersection avec l’axe des ordonnées (axe Y) au point (0,0).

$(0,0)$

Au lieu de cela, il intercepte périodiquement l’abscisse (axe X) à plusieurs coordonnées de pi.

$\displaystyle (k\pi ,0) \qquad k \in \mathbb{Z}$

La fonction est strictement croissante sur tout le domaine, elle n’a donc ni maximum ni minimum.

La dérivée de la tangente est :

$f(x)=\text{tg } x \ \longrightarrow \ f'(x)= 1+\text{tg}^2 x=\cfrac{1}{\text{cos}^2 x} =\text{sec}^2 x$

Enfin, l’intégrale de la fonction tangente est :

$\displaystyle \int \text{tg } x \ dx= -\ln \lvert \text{cos }x \rvert + C$

Période de la fonction tangente

Contrairement à d’autres fonctions trigonométriques telles que le sinus et le cosinus, la fonction tangente n’a pas d’amplitude puisqu’elle n’a ni valeur maximale ni valeur minimale. Cependant, c’est une fonction périodique, c’est-à-dire que ses valeurs se répètent selon une fréquence comme nous l’avons vu dans son graphique.

$\displaystyle f(x)= \text{tg}(wx)$

La période de la fonction tangente est la distance entre deux points auxquels le graphique est répété, et est calculée avec la formule suivante :

$\displaystyle \text{Periodo}=T=\cfrac{\pi}{w}$

théorème de tangente

Bien que la formule de la tangente soit normalement utilisée dans les triangles rectangles, il existe aussi un théorème à appliquer à tout type de triangle : le théorème de la tangente.

Le théorème de tangente relie les côtés et les angles de tout triangle comme suit :

$\displaystyle \cfrac{a+b}{a-b} = \cfrac{ \text{tg}\left(\frac{\alpha+\beta}{2}\right)}{\text{tg}\left(\frac{\alpha-\beta}{2}\right)}$

$\displaystyle \cfrac{a+c}{a-c} = \cfrac{ \text{tg}\left(\frac{\alpha+\gamma \vphantom{\beta}}{2}\right)}{\text{tg}\left(\frac{\alpha-\gamma\vphantom{\beta}}{2}\right)}$

$\displaystyle \cfrac{b+c}{b-c} = \cfrac{ \text{tg}\left(\frac{\beta+\gamma}{2}\right)}{\text{tg}\left(\frac{\beta-\gamma}{2}\right)}$

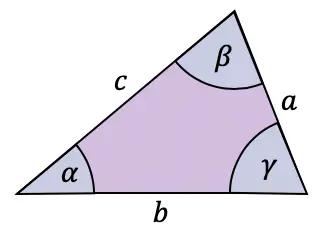
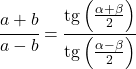
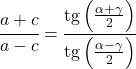
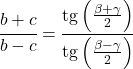
Relations de la fonction tangente avec d’autres rapports trigonométriques

Ci-dessous vous avez les relations de la tangente avec les rapports trigonométriques les plus importants de la trigonométrie.

Relation avec le sein

La tangente et le sinus d’un angle sont liés comme suit :

$\displaystyle \text{tg }\alpha = \pm \cfrac{\text{sen }\alpha }{\sqrt{1-\text{sen}^2\alpha \vphantom{\bigl( }}}$

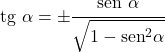
Rapport au cosinus

De même, la tangente et le cosinus d’un angle sont liés à l’égalité suivante :

$\displaystyle \text{tg }\alpha = \pm \cfrac{\sqrt{1-\text{cos}^2\alpha \vphantom{\bigl( }} }{\text{cos }\alpha}$

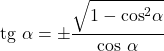
Relation avec la cosécante

Bien qu’il soit difficile à prouver, la tangente peut être résolue de manière à ce qu’elle ne dépende que de la cosécante :

$\displaystyle \text{tg }\alpha = \pm \cfrac{1}{\sqrt{\text{csc}^2\alpha -1 \vphantom{\bigl( }}}$

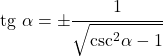
Relation avec la sécante

La tangente et la sécante d’un angle sont liées par l’équation suivante :

$\displaystyle \text{tg }\alpha = \pm\sqrt{\text{sec}^2\alpha -1$

Relation avec la cotangente

Tangente et cotangente sont des inverses multiplicatifs :

$\displaystyle \text{tg }\alpha =\pm \cfrac{1}{\text{cot }\alpha}$