Sur cette page, vous verrez comment calculer le rang d’un tableau en fonction d’un paramètre. Vous trouverez également des exemples et des exercices résolus étape par étape sur la façon de trouver la plage d’une matrice basée sur un paramètre.
Afin de bien comprendre la procédure d’étude du rang des matrices avec des paramètres, il est important que vous sachiez déjà comment calculer le rang d’une matrice par déterminants . Nous vous recommandons donc d’apprendre d’abord ces deux choses avant de continuer à lire.
Comment calculer la plage d’un tableau en fonction d’un paramètre. Exemple:
- Détermine la plage de la matrice A en fonction de différentes valeurs de paramètres
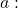
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0aa5688f2845a0225149f448466c943c_l3.png)
La matrice A sera de rang 3 au plus, car c’est une matrice d’ordre 3. Par conséquent, la première chose que nous devons faire est de résoudre le déterminant de toute la matrice 3×3 avec la règle de Sarrus , pour voir s’il peut être de rang 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-835a881061438326519f4660b4c394fc_l3.png)
Le résultat du déterminant est une fonction du paramètre
![]() . On fixe donc le résultat égal à 0 pour voir quand le tableau sera de rang 2 et quand il sera de rang 3 :
. On fixe donc le résultat égal à 0 pour voir quand le tableau sera de rang 2 et quand il sera de rang 3 :
![]()
Et on résout l’équation résultante :
![]()
![]()
![]()
Par conséquent, lorsque
![]() que ce soit +1 ou -1, le déterminant 3×3 sera 0 et, par conséquent, le rang de la matrice ne sera pas 3. En revanche, lorsque
que ce soit +1 ou -1, le déterminant 3×3 sera 0 et, par conséquent, le rang de la matrice ne sera pas 3. En revanche, lorsque![]() est différent de +1 et -1, le déterminant sera différent de 0 et, par conséquent, la matrice sera de rang 3.
est différent de +1 et -1, le déterminant sera différent de 0 et, par conséquent, la matrice sera de rang 3.
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-53dde6f61dc01cac5c0a0705c44a7433_l3.png)
Comme nous l’avons vu précédemment, lorsque
![]() est 1 le déterminant de la matrice est 0. Il ne peut donc pas être de rang 3. On essaie maintenant de calculer un déterminant 2×2 différent de 0 à l’intérieur de la matrice, par exemple celui du coin supérieur gauche :
est 1 le déterminant de la matrice est 0. Il ne peut donc pas être de rang 3. On essaie maintenant de calculer un déterminant 2×2 différent de 0 à l’intérieur de la matrice, par exemple celui du coin supérieur gauche :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d291f322f9d3f392e46568817e531a84_l3.png)
Le déterminant d’ordre 2 est différent de 0. Ainsi, lorsque le paramètre
![]() soit +1, le rang de la matrice sera 2 :
soit +1, le rang de la matrice sera 2 :
![]()
Une fois que nous avons vu la plage de la matrice lorsque
![]() et quand
et quand![]() Voyons ce qui se passe quand
Voyons ce qui se passe quand![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f723d9c6b9f786b8c405ac7ec2d8bf1d_l3.png)
Comme nous l’avons vu au début, quand
![]() es -1 el determinante de la matriz es 0. Por tanto, no puede ser de rango 3. Así que ahora tenemos que intentar encontrar algún determinante 2×2 dentro de la matriz que sea diferente de 0, por ejemplo el de la esquina inferior gauche:
es -1 el determinante de la matriz es 0. Por tanto, no puede ser de rango 3. Así que ahora tenemos que intentar encontrar algún determinante 2×2 dentro de la matriz que sea diferente de 0, por ejemplo el de la esquina inferior gauche:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdc9bd6d9ad083e1e38f53079aebb5e5_l3.png)
Le déterminant de la dimension 2 est différent de 0. Ainsi, lorsque le paramètre
![]() soit -1, le rang du tableau sera 2 :
soit -1, le rang du tableau sera 2 :
![]()
Nous avons donc trouvé 3 cas différents dans lesquels le rang de la matrice A dépend de la valeur que prend le paramètre
![]() Voici le résumé :
Voici le résumé :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc3a7ebea32c871ab7971a276decc60a_l3.png)
Maintenant que vous savez comment discuter de la gamme de matrices dépendantes des paramètres, vous pouvez vous entraîner à faire les exercices étape par étape ci-dessous. Pour les résoudre, les propriétés des déterminants vous aideront sûrement, donc si vous n’êtes pas très clair à leur sujet, je vous conseille de jeter d’abord un coup d’œil à la page liée, où chacun d’entre eux est expliqué avec des exemples.
Problèmes résolus de plage d’une matrice basée sur un paramètre
Exercice 1
Étudie la plage du tableau suivant en fonction de la valeur du paramètre
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d7f53b08bcf2e2660dbb7c0aeb6fd369_l3.png)
La matrice A aura au maximum le rang 3, car il s’agit d’une matrice 3×3. Par conséquent, la première chose que nous devons faire est de résoudre le déterminant de la matrice entière (avec la règle de Sarrus), pour voir s’il peut être de rang 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2539698cbcf9f06d2890d17da76174f_l3.png)
Nous définissons le résultat égal à 0 pour voir quand le tableau sera rang 2 et quand rang 3 :
![]()
![]()
![]()
Par conséquent, lorsque
![]() est différent de 2, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
est différent de 2, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c131e19dd5d5c0d7826306103b4e118b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b97f01989b5e9679f95d300cd64f3735_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-77b38ebf03b8ed059edefd523c5ca1f4_l3.png)
![]()
Nous avons donc trouvé 2 cas dans lesquels la plage de la matrice A varie avec la valeur que prend le paramètre :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-41e5cc7b6e9b3204f26e1c64e46f7057_l3.png)
Exercice 2
Trouvez la plage du tableau suivant en fonction de la valeur du paramètre
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b28f21cc2e7211d9dae9b6685b541fc_l3.png)
La matrice A aura au maximum le rang 3, car il s’agit d’une matrice 3×3. Par conséquent, la première chose que nous devons faire est de résoudre le déterminant de la matrice entière (avec la règle de Sarrus), pour voir s’il peut être de rang 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30c8c16fea09001059a5d66727fc7be3_l3.png)
Nous définissons le résultat égal à 0 pour voir quand le tableau sera rang 2 et quand rang 3 :
![]()
![]()
![]()
![]()
![]()
Par conséquent, lorsque
![]() est différent de +1 et -1, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
est différent de +1 et -1, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b95d408f076c4978c8605380a277cdf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcd50b9549925b5011a6c20943c326ee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03242296f208e07b9c4d634f0b7724cc_l3.png)
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2d16421400df26760d811229215ac83_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ecd0b86cd6c59a0911f0c39ca7599806_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-378e43f0ef61ccabf82dacb5ac70466f_l3.png)
![]()
Nous avons donc trouvé 3 cas dans lesquels la plage de la matrice A varie en fonction de la valeur que prend le paramètre :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bf1904cee51914e041d94f588fed84d_l3.png)
Exercice 3
Calcule la plage du tableau suivant en fonction de la valeur du paramètre
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-090a99d3b4111785433e5c769589eb01_l3.png)
La matrice A aura au maximum le rang 3, car il s’agit d’une matrice 3×3. Par conséquent, la première chose que nous devons faire est de résoudre le déterminant de la matrice entière (avec la règle de Sarrus), pour voir s’il peut être de rang 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fec1cb52bb87fa2bccb40b70e1f21c7c_l3.png)
Nous définissons le résultat égal à 0 pour voir quand le tableau sera rang 2 et quand rang 3 :
![]()
Il s’agit d’une équation quadratique incomplète, nous extrayons donc un facteur commun :
![]()
Et on fixe chaque terme égal à 0 :
![Rendered by QuickLaTeX.com \displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43b38da320da538e46c6b4515de48568_l3.png)
Nous avons obtenu comme solutions 0 et -4. Par conséquent, lorsque
![]() est différent de 0 et -4, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
est différent de 0 et -4, le déterminant 3×3 sera différent de 0 et, par conséquent, le rang de la matrice sera 3.
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d97b25f01cb00d4677da0de5b4340ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0f3c315588dff8274873001f727a69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c132b22650c707d9f410c3d9c1e8da35_l3.png)
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ce7e40d9d78ecddc5ee81fc799c8767_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-52d15d0bceeb1dbbc415fb4825ce9a05_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45971f1dbda32405246de38bb68bd92_l3.png)
![]()
Nous avons donc trouvé 3 cas dans lesquels la plage de la matrice A varie en fonction de la valeur que prend le paramètre :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-844f152985a2d84be1456501dfdc16e4_l3.png)
Exercice 4
Trouver l’étendue de la matrice suivante de dimension 3×4 selon la valeur du paramètre
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4da7907bd0e8f80006ea47d2437b3f3d_l3.png)
La matrice A sera au plus de rang 3, puisque nous ne pouvons calculer aucun déterminant 4×4 . Par conséquent, la première chose que nous devons faire est de résoudre tous les déterminants possibles d’ordre 3 (avec la règle de Sarrus), pour voir s’il peut être de rang 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2db025b8ecf4323d4a912d84a215d8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e40592bf6f8bfd13cb68a1fd0393cebb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce1c28ae4120f0b37059b763e576d2eb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-668e9096b00b90ee4cc48d272b17e7bd_l3.png)
Les résultats de tous les déterminants possibles d’ordre 3 sont 0, quelle que soit la valeur de
![]() . Ainsi la matrice ne sera jamais de rang 3, puisque peu importe la valeur qu’elle prend
. Ainsi la matrice ne sera jamais de rang 3, puisque peu importe la valeur qu’elle prend![]() qu’il n’y aura jamais de déterminant 3×3 différent de 0.
qu’il n’y aura jamais de déterminant 3×3 différent de 0.
Alors maintenant, nous essayons les déterminants de dimension 2 × 2. Cependant, tous les déterminants d’ordre 2 donnent également 0 sauf les suivants :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4408f1ccf562196943209356e50e892_l3.png)
Maintenant, nous définissons le résultat égal à 0 et résolvons l’équation :
![]()
![]()
![]()
Par conséquent, lorsque
![]() est différent de -2, le déterminant 2×2 sera différent de 0 et, par conséquent, le rang de la matrice sera 2.
est différent de -2, le déterminant 2×2 sera différent de 0 et, par conséquent, le rang de la matrice sera 2.
![]()
Voyons maintenant ce qui se passe quand
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ecbf63b188b46c05e67741cee83d7a2_l3.png)
Comme nous l’avons vu précédemment, lorsque
![]() est -2, tous les déterminants d’ordre 2 sont 0. Elle ne peut donc pas être de rang 2. Et comme il existe au moins un déterminant 1×1 différent de 0, dans ce cas le rang de la matrice est 1 :
est -2, tous les déterminants d’ordre 2 sont 0. Elle ne peut donc pas être de rang 2. Et comme il existe au moins un déterminant 1×1 différent de 0, dans ce cas le rang de la matrice est 1 :
![]()
Nous avons donc trouvé 2 cas dans lesquels la plage de la matrice A varie avec la valeur que prend le paramètre :
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-2bdfb67894431a4a08a3e791dcda0313_l3.png)