Sur cette page, vous apprendrez ce qu’est le déterminant d’une matrice 2×2. De plus, vous trouverez des exemples et des exercices résolus étape par étape sur la façon de résoudre les déterminants d’ordre 2, afin que vous puissiez le pratiquer et le comprendre parfaitement.
Qu’est-ce qu’un déterminant 2×2 ?
Un déterminant d’ordre 2 est une matrice de dimension 2 × 2 représentée par une barre verticale de chaque côté de la matrice. Par exemple, si nous avons la matrice suivante :
![\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50ff006696d04e4eee005e245ba217e4_l3.png "Rendered by QuickLaTeX.com")
Le déterminant de la matrice A est représenté comme suit :
![\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc95ca8f173419691852fd137d67154_l3.png "Rendered by QuickLaTeX.com")
Comme vous l’avez vu, écrire le déterminant d’une matrice carrée 2×2 est facile. Voyons maintenant comment il est calculé :
Comment résoudre un déterminant d’ordre 2 ?
Pour calculer le déterminant d’une matrice 2×2, nous devons multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire.
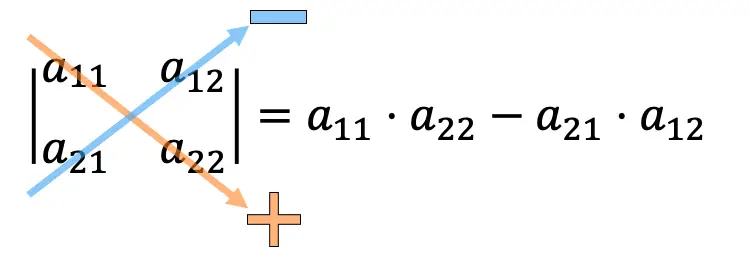
Exemples de calcul de déterminants 2×2 :
![\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-228cbdabc4e6d330b56fae20f5163e64_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e9aed81d00e74873a5e797746861a51_l3.png "Rendered by QuickLaTeX.com")
Problèmes résolus de déterminants de matrices 2 × 2
Exercice 1
Calculez le déterminant 2×2 suivant :
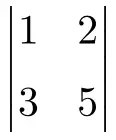
Pour faire un déterminant 2×2, il faut multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire :
![\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d03764083647c0b05f9a5d7266c8915_l3.png "Rendered by QuickLaTeX.com")
Exercice 2
Résolvez le déterminant suivant de dimension 2×2 :
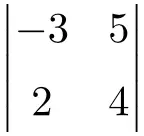
Pour trouver la solution d’un déterminant d’ordre 2 il faut multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire :
![\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56c917d70b8c6ec3697612d44f84e522_l3.png "Rendered by QuickLaTeX.com")
Exercice 3
Trouver la solution du déterminant d’ordre 2 suivant :
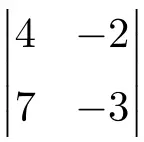
Pour trouver la solution d’un déterminant de dimension 2, il faut multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire :
![\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cbd06fd83283d3e82105c24eaf95af9f_l3.png "Rendered by QuickLaTeX.com")
Exercice 4
Calculez le déterminant 2×2 suivant :
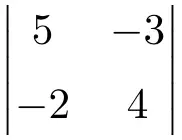
Pour calculer les déterminants des matrices 2×2, nous devons multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire :
![\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34915d9aff298587a13346c6fc30bfcd_l3.png "Rendered by QuickLaTeX.com")
Exercice 5
Déterminez le résultat du déterminant 2×2 suivant :
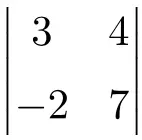
Pour trouver la solution d’un déterminant 2×2, nous devons multiplier les éléments de la diagonale principale et soustraire le produit de la diagonale secondaire :
![\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c6e4a7fdc04f0458d95c1d62b12d7ac_l3.png "Rendered by QuickLaTeX.com")
Brillant! Vous savez maintenant comment créer des déterminants de dimension 2×2 ! Maintenant, vous êtes sûrement déjà en mesure de comprendre comment le déterminant 3×3 est calculé et aussi comment le déterminant d’une matrice 4×4 est résolu.