Propriétés des déterminants

Dans cette section, nous allons voir quelles sont toutes les propriétés des déterminants . Nous démontrons également chaque propriété avec un exemple afin que vous les compreniez parfaitement. Et, en plus, vous trouverez des exercices liés aux propriétés des déterminants.

Ci-dessous, nous allons expliquer chaque propriété des déterminants un par un, mais si vous préférez, vous pouvez passer directement au tableau récapitulatif ci-dessous. 😉

Propriété 1 : Déterminant de la matrice transposée

Le déterminant d’une matrice est équivalent au déterminant de sa matrice transposée.

$\lvert A \rvert = \lvert A^t \rvert$

Exemple:

$\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}$

Maintenant, nous transposons la matrice 2×2 et résolvons le déterminant. Remarquez que nous obtenons le même résultat que précédemment :

$\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}$

Propriété 2 : Déterminant avec une ligne ou une colonne remplie de zéros

Si un déterminant a une ligne ou une colonne remplie de zéros, le déterminant renvoie 0.

$\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0$

Exemple:

$\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}$

Dans ces deux exemples, les déterminants sont évalués à 0. Parce que la deuxième ligne du premier déterminant est entièrement composée de zéros et que la troisième colonne du deuxième déterminant est également entièrement composée de zéros.

Propriété 3 : Déterminant avec deux lignes ou colonnes égales

Si un déterminant a deux lignes égales ou multiples ou deux colonnes, le déterminant est égal à zéro (0).

Par conséquent, s’il existe une combinaison linéaire entre les lignes ou les colonnes, c’est-à-dire qu’elles sont linéairement dépendantes, le déterminant donne 0.

Exemple:

$\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0$

Dans ce cas, le déterminant donne 0 car les colonnes 2 et 3 sont égales.

Propriété 4 : Modifier les lignes ou les colonnes d’un déterminant

Si deux lignes ou deux colonnes sont modifiées l’une par rapport à l’autre, le déterminant donne le même résultat mais avec un signe différent.

$\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}$

Exemple:

$\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}$

Maintenant, nous changeons l’ordre des colonnes 2 et 3 l’une par rapport à l’autre. Notez que le résultat est le même mais avec un signe différent :

$\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}$

Propriété 5 : Multiplier une ligne d’un déterminant par un scalaire

Multiplier tous les éléments d’une ligne entière ou d’une colonne entière par un nombre réel revient à multiplier le résultat du déterminant par ce nombre.

$\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

$\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

Exemple:

$\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}$

Maintenant nous prenons le même déterminant et multiplions une ligne entière par 2. Vous verrez que le résultat sera celui du déterminant précédent mais multiplié par 2, soit 10 :

$\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}$

Propriété 6 : Déterminant du produit matriciel

Le déterminant du produit de deux matrices est égal au produit du déterminant de chaque matrice séparément.

$\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert$

Exemple:

Pour démontrer cette propriété des déterminants, nous allons calculer le déterminant de la multiplication des deux matrices suivantes de deux manières possibles :

$\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}$

Nous ferons d’abord la multiplication des deux matrices, puis nous calculerons le déterminant de la matrice résultante :

$\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}$

Maintenant, nous calculons le déterminant de chaque matrice séparément, puis multiplions les résultats :

$\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}$

Comme vous pouvez le voir, faire d’abord le produit matriciel puis le déterminant donne le même résultat que de faire d’abord le déterminant de chaque matrice, puis de multiplier les résultats.

En revanche, cette condition ne s’applique pas aux opérations d’addition et de soustraction, c’est-à-dire que le déterminant de l’addition (ou de la soustraction) de deux matrices ne donne pas le même résultat que l’addition (ou la soustraction) des déterminants de deux matrices séparément.

Propriété 7 : Déterminant de la matrice inverse

Si une matrice est inversible, le déterminant de son inverse correspond à l’inverse du déterminant de la matrice d’origine.

$\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}$

Exemple:

Nous allons vérifier cette propriété en calculant d’abord l’inverse d’une matrice puis en résolvant son déterminant. Nous verrons que le résultat équivaut à trouver le déterminant de la matrice d’origine et à l’inverser.

Nous inversons donc la matrice suivante et calculons son déterminant :

$\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}$

$\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}$

$\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}$

Et maintenant, nous résolvons le déterminant de la matrice d’origine et faisons son inverse :

$\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2$

$\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}$

Comme vous pouvez le voir, les résultats des deux opérations sont identiques. La propriété est donc prouvée.

Propriété 8 : Remplacer la ligne d’un déterminant

La ligne d’un déterminant peut être remplacée par l’addition (ou la soustraction) de la même ligne plus (ou moins) une autre ligne multipliée par un nombre.

Exemple:

Avec l’exemple suivant, nous allons vérifier cette propriété. Nous allons d’abord calculer un déterminant, puis nous allons opérer sur une ligne du déterminant et recalculer son résultat. Vous verrez comment on obtient le même résultat dans les deux cas.

Donc, calculons d’abord un déterminant 3×3 avec la règle de Sarrus :

$\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}$

Maintenant, à la ligne 2, nous ajoutons la première ligne multipliée par 2 :

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}$

Et on résout le déterminant après avoir transformé une de ses lignes :

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}$

Dans les deux cas, le résultat a été -3. Ainsi, il est démontré que le résultat d’un déterminant ne change pas si une ligne est remplacée par la somme de la même ligne plus une autre ligne multipliée par un nombre.

Propriété 9 : Déterminant d’une matrice triangulaire

Le déterminant d’une matrice triangulaire est le produit des éléments de sa diagonale principale.

Exemple:

Nous allons résoudre le déterminant de la matrice triangulaire suivante à titre d’exemple :

$\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}$

Propriété 10 : Déterminant d’une matrice diagonale

Le déterminant d’une matrice diagonale est égal à la multiplication des éléments de sa diagonale principale.

Exemple:

Prenons comme exemple le déterminant de la matrice diagonale suivante :

$\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}$

Tableau récapitulatif des propriétés des déterminants

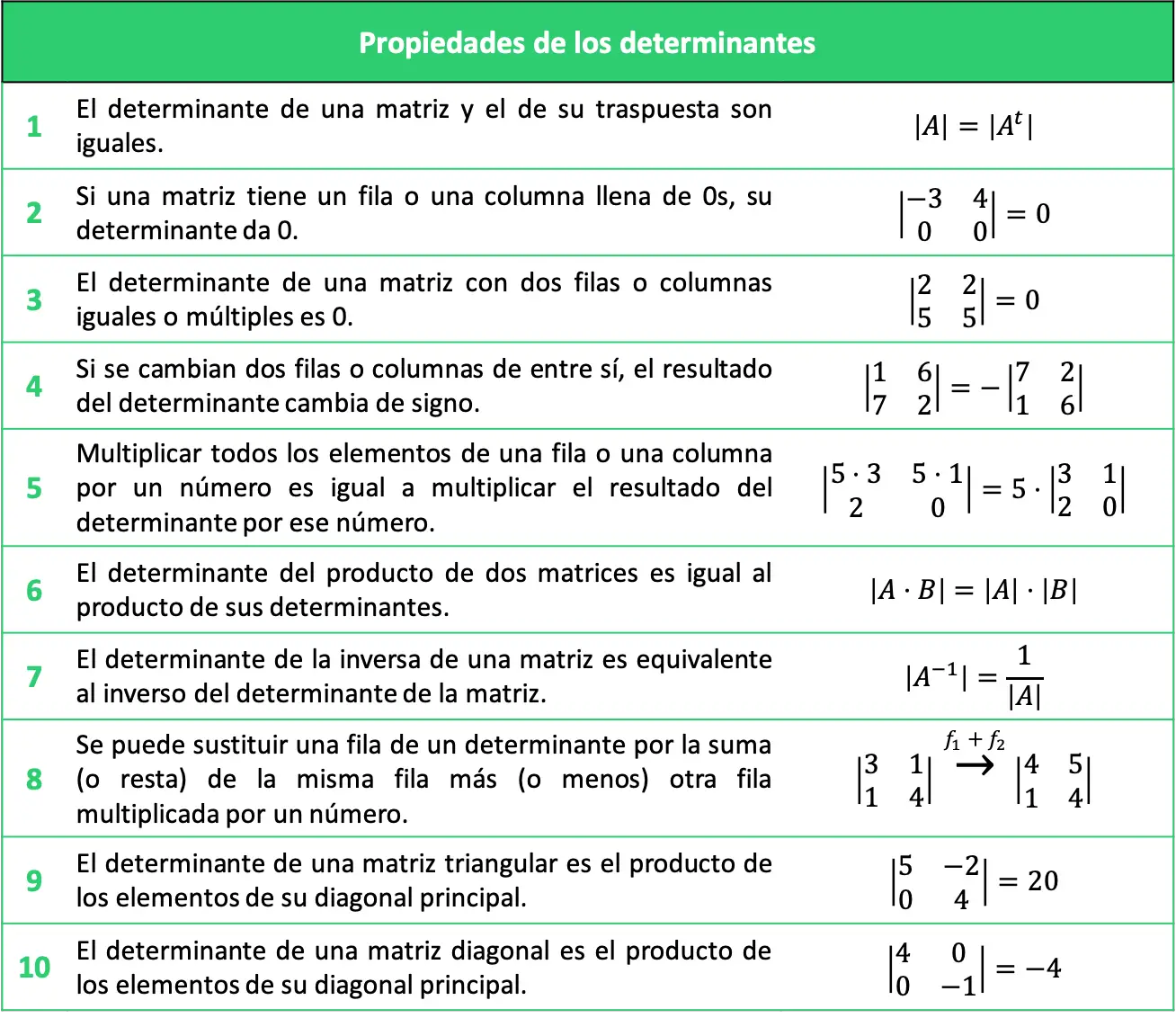
Les propriétés des déterminants expliquées peuvent être résumées dans le tableau suivant :

Exercices résolus avec les propriétés des déterminants

Exercice 1

Résolvez le déterminant suivant :

$\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}$

voir solution

Si un déterminant a une ligne ou une colonne remplie de zéros, le déterminant renvoie 0 (propriété 2). Par conséquent, le résultat du déterminant est 0, car la troisième colonne est remplie de zéros.

Exercice 2

Résolvez le déterminant suivant :

$\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}$

voir solution

Si un déterminant a deux lignes égales ou multiples ou deux colonnes, le déterminant renvoie 0 (propriété 3). Par conséquent, le résultat du déterminant est 0, car la première ligne et la troisième ligne sont égales.

Exercice 3

Calculez le déterminant suivant :

$\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}$

voir solution

Si un déterminant a deux lignes égales ou multiples ou deux colonnes, le déterminant renvoie 0 (propriété 3). Par conséquent, le résultat du déterminant est 0, car la quatrième colonne est le double de la première colonne.

Exercice 4

On connaît le résultat d’un déterminant, bien qu’on ne connaisse pas les éléments de la matrice :

$\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3$

À partir du résultat du déterminant précédent et des propriétés des déterminants, calculez le résultat des déterminants suivants :

$\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}$

voir solution

pour)

$\begin{pmatrix} a & c \\ b & d \end{pmatrix}$ est la matrice transposée de $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ . Et le déterminant d’une matrice est égal au déterminant de sa matrice transposée (propriété 1). Par conséquent, le résultat de ce déterminant est également 3.

$\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}$

b) Dans le déterminant

$\begin{vmatrix} b & a \\ d & c \end{vmatrix}$ les colonnes 1 et 2 ont été modifiées par rapport au déterminant de l’énoncé $\begin{vmatrix} a & b \\ c & d \end{vmatrix}$ . Par conséquent, selon la propriété 4, le résultat est le même que le résultat du déterminant de l’énoncé mais avec un signe différent, c’est-à-dire -3.

$\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}$

c) Dans le déterminant

$\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}$ toute la deuxième colonne du déterminant de l’énoncé a été multipliée par 3. Par conséquent, de la propriété 5, on peut déduire que son résultat sera également le résultat du déterminant de l’énoncé multiplié par 3, soit 9.

$\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}$

Exercice 5

On connaît le résultat de ces deux déterminants :

$\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8$

$\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4$

A partir de ces informations, calculez :

$\displaystyle \vert A \cdot B \vert$

voir solution

Pour calculer le résultat du déterminant, il n’est pas nécessaire de multiplier les matrices 4×4. Puisque le déterminant du produit de deux matrices est égal au produit du déterminant de chaque matrice séparément (propriété 6). Pourtant:

$\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}$

Propriété 1 : Déterminant de la matrice transposée

Exemple:

Propriété 2 : Déterminant avec une ligne ou une colonne remplie de zéros

Exemple:

Propriété 3 : Déterminant avec deux lignes ou colonnes égales

Exemple:

Propriété 4 : Modifier les lignes ou les colonnes d’un déterminant

Exemple:

Propriété 5 : Multiplier une ligne d’un déterminant par un scalaire

Exemple:

Propriété 6 : Déterminant du produit matriciel

Exemple:

Propriété 7 : Déterminant de la matrice inverse

Exemple:

Propriété 8 : Remplacer la ligne d’un déterminant

Exemple:

Propriété 9 : Déterminant d’une matrice triangulaire

Exemple:

Propriété 10 : Déterminant d’une matrice diagonale

Exemple:

Tableau récapitulatif des propriétés des déterminants

Exercices résolus avec les propriétés des déterminants

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply