Théorème des facteurs

Sur cette page, nous expliquons ce qu’est le théorème des facteurs. De plus, nous montrons à quoi sert le théorème des facteurs : divisibilité des polynômes, trouver des racines, factoriser des polynômes,… Enfin, vous pourrez vous entraîner avec des exercices résolus pas à pas sur le théorème des facteurs.

Quel est le théorème des facteurs ?

En mathématiques, le théorème des facteurs dit qu’un polynôme P(x) est divisible par un autre polynôme de la forme (xa) si et seulement si P(a)=0.

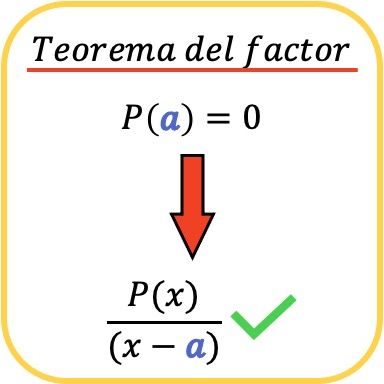
De même, en conséquence du théorème des facteurs, il s’ensuit que si un polynôme P(x) est divisible par le terme (x−a), cela signifie que la valeur a est une racine (ou zéro) du polynôme P(x) .

Qu’un polynôme soit divisible par un autre signifie que le reste (ou reste) de la division entre les deux polynômes est égal à zéro. Au cas où vous ne vous souviendriez pas complètement de ce concept, dans le lien suivant, vous pouvez voir des exemples de division de polynômes , vous y trouverez également l’explication de la façon de diviser des polynômes et des exercices résolus étape par étape.

Exemples de théorème des facteurs

Maintenant que nous connaissons la définition mathématique du théorème des facteurs, examinons plusieurs exemples pour voir comment il est appliqué.

Exemple 1

L’une des applications du théorème des facteurs est de savoir si un polynôme donné est divisible par un binôme . Voyons un exemple de la façon dont cela est fait avec le théorème du facteur :

• Déterminer si le polynôme P(x) est divisible par le binôme Q(x), les deux étant :

Premièrement, le polynôme diviseur, Q(x), est un polynôme de type (xa), nous pouvons donc appliquer le théorème des facteurs pour résoudre le problème.

Donc, pour vérifier si P(x) peut être divisé par Q(x) nous devons calculer la valeur numérique du polynôme P(x) pour x=1, puisque 1 est le terme indépendant du polynôme diviseur avec son signe changé :

La valeur numérique du polynôme P(x) à x = 1 donne zéro, donc selon le théorème du facteur P(x) est divisible par Q(x), ou en d’autres termes, le reste de la division par les deux sera nul.

On peut vérifier que la condition de divisibilité est satisfaite en divisant les 2 polynômes par le théorème de Ruffini :

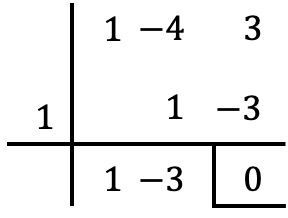
Comme vous pouvez le voir dans cet exemple, le théorème du facteur est un cas particulier du théorème du reste (ou reste). Je vous laisse cet article qui explique ce qu’est le théorème du reste , vous trouverez également des exemples et des exercices résolus avec. Et, en plus, vous pourrez voir quelle est la différence entre le théorème des restes et le théorème des facteurs.

Exemple 2

Le théorème des facteurs peut également être utilisé pour trouver les racines (ou les zéros) d’un polynôme. Mais, évidemment, pour comprendre ce type de problème, vous devez savoir quelles sont les racines d’un polynôme . Si vous ne maîtrisez toujours pas ce concept, vous pouvez jeter un œil à la page liée, qui est expliquée en détail.

Voyons donc à travers un exemple comment le théorème des facteurs est appliqué pour trouver une racine d’un polynôme :

• Étant donné le polynôme P(x), calculez si l’une de ses racines est x=2 :

En appliquant le théorème du facteur, le terme x=2 ne sera une racine du polynôme P(x) que si la valeur numérique de P(x) pour x=2 est nulle. Nous devons donc trouver cette valeur numérique :

En effet, la valeur numérique du polynôme P(x) s’annule en x=2, donc grâce au théorème des facteurs on peut affirmer que x=2 est une racine du polynôme P(x).

Factorisation de polynômes à l’aide du théorème factoriel

Une autre application du théorème des facteurs est la factorisation des polynômes . Au cas où vous ne sauriez pas en quoi il consiste, factoriser un polynôme signifie transformer l’expression d’un polynôme en un produit de facteurs, c’est-à-dire que factoriser un polynôme simplifie son expression algébrique.

Ainsi, le théorème factoriel établit que si un polynôme P(x) vérifie P(a)=0 pour une valeur a donnée, alors l’expression dudit polynôme peut être factorisée en le produit P(x)=(xa)· Q( x), où Q(x) est le polynôme résultant de la division du polynôme P(x) par (xa).

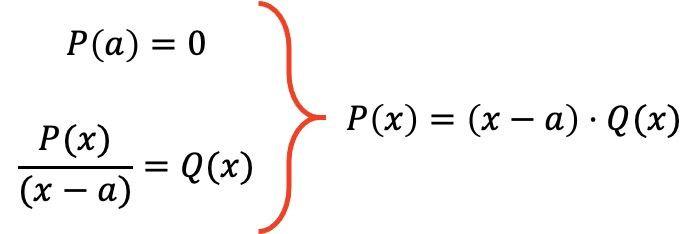
A titre d’exemple, nous allons factoriser le polynôme suivant à l’aide du théorème factoriel :

Du polynôme précédent, nous pouvons savoir que x=-2 est l’une de ses racines, puisque la valeur numérique du polynôme pour x=-2 est égale à zéro :

On divise donc avec la règle de Ruffini le polynôme P(x) entre le binôme formé par x et cette racine changée de signe, c’est-à-dire le facteur (x+2) :

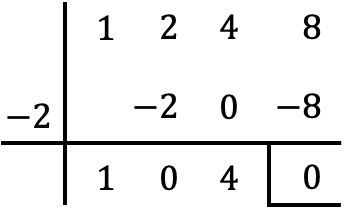
Donc le quotient de la division polynomiale est :

Et enfin, à partir du théorème des facteurs, on peut exprimer le polynôme P(x) sous la forme d’une multiplication du facteur (x+2) par le quotient obtenu à la division précédente :

Nous avons ainsi factorisé le polynôme P(x), mais seulement partiellement. Afin de factoriser complètement un polynôme, une procédure plus longue doit être appliquée. Nous avons fait un guide où nous enseignons pas à pas comment factoriser les polynômes de Ruffini , de plus, dans cet article, nous avons expliqué tous les types de factorisations et vous pourrez vous entraîner avec des exercices résolus. Alors cliquez sur le lien pour découvrir comment factoriser un polynôme à partir de l’ensemble.

Problèmes résolus du théorème des facteurs

Ensuite, nous avons préparé plusieurs exercices résolus étape par étape sur le théorème des facteurs afin que vous puissiez vous entraîner, et ainsi vérifier si vous avez bien compris ce théorème. Nous vous recommandons d’essayer de les faire vous-même, puis de voir si vous avez bien compris la solution. N’oubliez pas non plus que vous pouvez nous laisser vos questions ci-dessous dans les commentaires ! ❓❓💬💬

Exercice 1

Utilisez le théorème factoriel pour trouver si le polynôme P(x) est divisible par le binôme Q(x) et, si c’est le cas, trouvez une racine du polynôme et factorisez-la.

Dans ce cas, le polynôme diviseur Q(x) est un binôme composé uniquement d’un x et d’un terme indépendant. Donc pour montrer que le polynôme P(x) peut être divisé par l’autre polynôme Q(x) avec le théorème factoriel, il faut évaluer la valeur numérique du polynôme P(x) dans le terme indépendant du polynôme diviseur changé de signe, c’est-à-dire à x=3 :

La valeur numérique du polynôme P(x) en x=3 est équivalente à 14, c’est-à-dire qu’elle est différente de zéro. Ainsi, selon le théorème du facteur, P(x) n’est PAS divisible par Q(x) car le reste de la division n’est pas nul.

Exercice 2

Découvrez par le théorème factoriel si le polynôme P(x) est divisible par le binôme Q(x) et, si oui, trouvez une racine du polynôme P(x) et factorisez-la.

Dans ce cas le polynôme diviseur Q(x) est un binôme composé uniquement d’un x et d’un terme indépendant, on peut donc appliquer le théorème factoriel.

Et pour vérifier si le polynôme P(x) peut être divisé par le polynôme Q(x), il faut trouver la valeur numérique du polynôme P(x) pour le terme indépendant du polynôme Q(x) changé de signe, c’est-à-dire , en x=-1 :

Dans ce problème, la valeur numérique du polynôme en x=-1 est zéro, donc P(x) est divisible par Q(x).

Alors, on peut déduire par le théorème factoriel que x=-1 est une racine du polynôme P(x), puisque la valeur numérique de P(x) en x=-1 s’annule.

Ainsi, puisque x=-1 est une racine du polynôme P(x), pour le factoriser il suffit de le diviser par x+1. Et, pour cela, nous allons utiliser la méthode Ruffini :

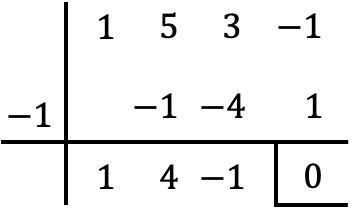
Donc le résultat de l’opération est :

On peut donc factoriser le polynôme P(x) comme suit :

Exercice 3

Trouvez avec le théorème factoriel si le polynôme P(x) est divisible par le binôme Q(x) et, si oui, trouvez également une racine du polynôme P(x) et factorisez-la.

Dans ce cas, le polynôme qui divise Q(x) est un binôme formé uniquement par un x et un terme indépendant, nous pouvons donc utiliser le théorème des facteurs.

Et pour vérifier si le polynôme P(x) est divisible par le polynôme Q(x), il faut déterminer la valeur numérique du polynôme P(x) pour le terme indépendant du polynôme Q(x) changé de signe, c’est-à-dire en x =-3 :

Dans ce cas, la valeur numérique du polynôme en x=-3 est nulle, donc effectivement P(x) est divisible par Q(x).

Pour cette raison, on déduit du théorème factoriel que x=-3 est une racine du polynôme P(x), puisque P(-3) est égal à zéro.

Donc, puisque x=-3 est une racine du polynôme P(x), pour le factoriser il faut le diviser par x+3. Et, pour cela, nous utiliserons la règle de Ruffini :

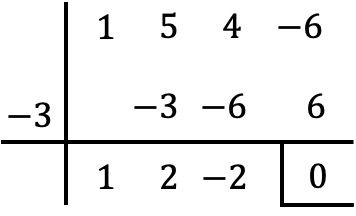
Donc le résultat de la division est :

Et, par conséquent, on peut factoriser le polynôme P(x) de la manière suivante :

Que pensez-vous du théorème des facteurs ? Pensez-vous que c’est utile en algèbre? On vous lit dans les commentaires !
👀⬇⬇⬇👀