Vous trouverez ici l’explication de ce qu’est le théorème des restes (ou théorème des restes) et comment il est appliqué aux polynômes. Vous pourrez également voir des exemples et, en plus, vous entraîner avec des exercices résolus étape par étape sur le théorème des restes.
Quel est le théorème des restes ?
En mathématiques, le théorème des restes dit que le reste de la division de tout polynôme P(x) par un autre polynôme de la forme (xa) est égal à la valeur numérique du polynôme P(x) pour la valeur x=a, soit Autrement dit, le reste de la division P(x):(xa) est équivalent à P(a).

Exemple du théorème des restes
Une fois que nous avons vu en quoi consiste le théorème des restes, voyons un exemple pratique de son application :
- Calculez le reste de la division entre les deux polynômes suivants :
![]()
![]()
Pour trouver le reste (ou résidu) de la division polynomiale on peut profiter du théorème du reste, car dans ce cas le polynôme diviseur est de la forme (xa), c’est-à-dire qu’il est du premier degré, le coefficient du la variable x vaut 1 et a un terme indépendant.
Nous appliquons donc le théorème des restes, qui dit que le reste d’une division comme celle-ci est égal à la valeur numérique du polynôme dividende évalué dans le terme indépendant du polynôme diviseur changé de signe, c’est-à-dire P(1).

Par conséquent, pour trouver le reste de la division, nous devons évaluer le polynôme en x=1 :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff03f53066d698ee3d76e0024f3b51ac_l3.png)
Le reste de la division entre les polynômes est donc 2 .
D’un autre côté, on peut aussi vérifier avec la règle de Ruffini pour diviser les polynômes que le reste coïncide avec le résultat que nous avons trouvé :
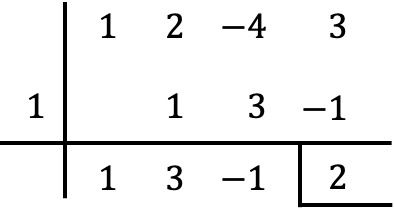
Comme vous pouvez le constater, il est beaucoup plus rapide et plus facile de déterminer le reste d’une division d’un polynôme par un binôme avec le théorème des restes qu’avec la règle de Ruffini, car beaucoup moins de calculs sont effectués.
Théorème du reste et des facteurs
Du théorème des restes et de la définition de la racine (ou zéro) d’un polynôme on peut déduire le théorème des facteurs. Ainsi, le théorème des facteurs implique ce qui suit :
Le théorème des facteurs dit qu’un polynôme P(x) est divisible par un autre polynôme de la forme (xa) si, et seulement si, P(a)=0. Et, dans ce cas, cela signifie que a est une racine ou un zéro du polynôme P(x).
De plus, selon le théorème des restes, cela signifie que si un polynôme est divisible par un autre polynôme, le reste de ladite division est nul, puisque P(a)=0.
Par exemple, si nous avons un certain polynôme :
![]()
Ce polynôme est divisible par le binôme (x-2) car P(2)=0 :
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e90c14ff06cdfa041299e016051b1dd_l3.png)
Puisque x=2 annule le polynôme P(x), cela signifie que x=2 est une racine dudit polynôme.
Et de plus, puisque P(2)=0, on peut savoir grâce au théorème des restes que le reste de la division
![]() est égal à 0.
est égal à 0.
Exercices résolus du théorème des restes
Pour finir de comprendre le théorème des restes, nous vous avons préparé quelques exercices résolus étape par étape afin que vous puissiez vous entraîner. Nous vous conseillons d’essayer d’abord l’exercice par vous-même, puis de vérifier si vous l’avez fait correctement.
Exercice 1
Trouver, par le théorème des restes, le reste de la division polynomiale
![]() , étant les polynômes impliqués dans l’opération :
, étant les polynômes impliqués dans l’opération :
![]()
Le polynôme diviseur est composé uniquement d’un terme du premier degré et d’un terme indépendant et, de plus, le coefficient du terme du premier degré est 1. On peut donc utiliser le théorème des restes.
Et pour appliquer le théorème des restes, il suffit d’évaluer le polynôme dividende dans le terme indépendant du polynôme diviseur changé de signe, ou en d’autres termes, il faut calculer P(2).
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23790b78a8463a23a7b8202ab544ade9_l3.png)
Le reste de la division entre les deux polynômes est donc 21 .
Exercice 2
Étant donné le polynôme
![]() Trouvez le reste obtenu en le divisant par chacun des polynômes suivants :
Trouvez le reste obtenu en le divisant par chacun des polynômes suivants :
Puisque tous les polynômes diviseurs satisfont aux conditions du théorème du reste, nous pouvons utiliser ce théorème pour déterminer le reste de chaque division :
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8ae7d7c667bf9ca6bd7417356756447_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2a31e7c1334f8d1a24ba246d0459e4e_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e8191f6ce490a0786515d84efaf45ec_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d2e1e17bbcf91abb36d8cad24cadf0c_l3.png)
Exercice 3
Calculer combien doit valoir le paramètre
![]() de sorte que le reste de la division des polynômes
de sorte que le reste de la division des polynômes![]() être égal à 3, les deux étant des polynômes :
être égal à 3, les deux étant des polynômes :
![]()
Dans ce cas particulier, le polynôme qui divise est formé d’un monôme du premier degré et d’un terme indépendant et, de plus, le coefficient du monôme du premier degré est 1. On peut donc utiliser le théorème du reste.
Et pour utiliser le théorème des restes, il suffit de remplacer le terme indépendant du polynôme diviseur par un changement de signe où dans le polynôme divisé il y a un x, il faut donc résoudre P(-3).
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-693cd65a618f884d0dd1be2f20594229_l3.png)
Mais évidemment on obtient un résultat basé sur l’inconnue
![]() Cependant, l’énoncé du problème nous dit que le reste doit être égal à trois, nous devons donc définir le reste trouvé égal à 3 :
Cependant, l’énoncé du problème nous dit que le reste doit être égal à trois, nous devons donc définir le reste trouvé égal à 3 :
![]()
Et enfin, on résout l’équation :
![]()
![]()
![]()
![]()
Exercice 4
Déterminer avec le théorème du facteur et du reste si le polynôme
![]() est divisible par le polynôme
est divisible par le polynôme ![]()
![]()
Pour que le polynôme
![]() être divisible par le polynôme
être divisible par le polynôme![]() la division entre ces deux polynômes doit être exacte et donc le reste doit être nul.
la division entre ces deux polynômes doit être exacte et donc le reste doit être nul.
Alors, puisque le polynôme diviseur est
![]() Par le théorème des facteurs et le théorème des restes, nous savons que le polynôme
Par le théorème des facteurs et le théorème des restes, nous savons que le polynôme![]() sera divisible par le polynôme
sera divisible par le polynôme![]() s’il est rempli
s’il est rempli![]() Il faut donc voir si cette égalité est vérifiée :
Il faut donc voir si cette égalité est vérifiée :
![]()
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e8793835809000092b15eaec3877c18_l3.png)
En effet, le reste de la division
![]() est égal à 0, donc le polynôme
est égal à 0, donc le polynôme![]() Oui, il est divisible par l’autre polynôme
Oui, il est divisible par l’autre polynôme ![]()
Qu’avez-vous pensé de l’explication ? Avez-vous apprécié? Esperons-le! N’oubliez pas que vous pouvez nous laisser vos suggestions ou questions dans les commentaires. ⬇⬇⬇ On vous lit tous ! 😁😁