Binômes - Mathority

Sur cette page, vous trouverez une explication de ce qu’est un binôme et, en plus, vous pourrez voir des exemples de chaque type de binôme. Aussi, nous vous montrons les formules qui sont utilisées pour résoudre des opérations avec des binômes : multiplication de binômes, binôme au carré, binôme au cube,…

Qu’est-ce qu’un binôme ?

En algèbre, la définition d’un binôme est la suivante :

Un binôme est un polynôme composé de seulement deux monômes . Autrement dit, un binôme consiste en une expression algébrique avec seulement 2 termes différents qui sont joints par le signe plus (+) ou le signe moins (-).

Le mot binôme vient du grec et est composé de deux composantes lexicales ( bi et nomos ), qui signifient ce qui suit :

bi : préfixe signifiant 2.
nomos : signifie partie.

On peut donc en déduire le sens du binôme : polynôme à deux parties (ou 2 monômes).

D’autre part, le concept de binôme a une autre signification que celle mathématique, à savoir qu’un binôme peut également désigner un ensemble de deux personnalités qui ont un rôle de premier plan dans la vie politique, dans certaines disciplines sportives ou même dans le divertissement. . Mais, évidemment, nous nous concentrerons ici sur la définition mathématique du binôme.

Exemples de binômes

Pour finir de comprendre la notion de binôme, nous allons voir plusieurs exemples de ce type de polynôme :

Exemple de binôme du second degré :

$x^2+4x$

Exemple de binôme du troisième degré :

$x^3+5$

Exemple de binôme du quatrième degré :

$3x^4+8x^2$

Maintenant que nous savons en quoi consiste un binôme, nous allons voir les différents types de binômes qu’il existe et comment les opérations avec les binômes sont résolues.

binôme au carré

Un binôme au carré est une identité remarquable, également appelée produit remarquable ou égalité remarquable. Résoudre la puissance d’un binôme élevé à 2 dépend s’il s’agit d’un binôme somme ou d’un binôme différence.

Un binôme somme fait référence à ce binôme dont les deux termes sont positifs, c’est-à-dire qu’un binôme somme carré est :

$(a+b)^2$

D’autre part, un binôme de différence (ou de soustraction) est le conjugué du binôme d’addition, c’est-à-dire que l’un de ses monômes a un signe négatif. Par conséquent, l’expression algébrique d’une différence binomiale au carré est :

$(a-b)^2$

Pour calculer un binôme au carré, il faut appliquer une formule qui, comme nous l’avons vu, varie selon qu’il s’agit d’une addition ou d’une soustraction. Découvrez comment cela se fait dans les formules des égalités notables , où vous pourrez voir toutes les explications étape par étape ainsi que des exemples et des exercices résolus, et pas seulement de ces 2 égalités notables mais de toutes.

binôme au cube

Bien qu’ils soient moins souvent utilisés, les binômes en cubes sont également considérés comme des produits notables. Ou en d’autres termes, il existe des règles mathématiques qui permettent de trouver rapidement le cube d’un binôme (vous pouvez les voir dans le lien ci-dessus des formules d’identités notables ).

Comme précédemment, le résultat de cette potentialisation dépend s’il s’agit du cube d’une somme :

$(a+b)^3$

Ou si, au contraire, la puissance est constituée par le cube d’une différence ou d’une soustraction :

$(a-b)^3$

Logiquement, la principale différence entre un binôme au carré et un binôme au cube est l’exposant de la puissance. Cependant, la formule d’un binôme au cube est beaucoup plus compliquée que celle d’un binôme au carré.

des accords notables

Il existe en particulier certains types de binômes qui sont un peu particuliers de par leurs caractéristiques, puisqu’ils correspondent à des identités notables (ou produits notables) moins connues.

Somme des carrés: $a^2+b^2$
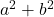
Différence (ou soustraction) de carrés : $a^2-b^2$
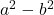
Somme des cubes : $a^3+b^3$
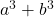
Différence (ou soustraction) de cubes : $a^3-b^3$

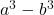
Où

$a$ et $b$ sont deux monômes quelconques.

Bien que ces expressions binomiales ressemblent beaucoup à celles que nous avons vues juste au-dessus (binôme au carré et binôme au cube), si vous regardez attentivement, elles sont différentes. En ce sens, vous pouvez également voir les formules des binômes notables et leurs déductions en cliquant sur le lien au-dessus des ⬆ formules des identités notables .⬆

multiplication binomiale

L’une des opérations les plus courantes avec les binômes est la multiplication. Donc, ensuite, nous allons voir un exemple de la façon de calculer une multiplication entre des binômes.

$(x^2+2x)\cdot (x-5)$

Pour calculer la multiplication binomiale, nous devons d’abord multiplier chaque terme du premier binôme par chaque terme du second binôme :

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Ensuite, nous regroupons les termes similaires, c’est-à-dire qu’ils ont la même partie littérale :

$\bm{x^3-3x^2 -10x}$

Et de cette façon, nous avons réussi à trouver le résultat du produit entre les binômes.

Produit de deux binômes avec un terme commun

Lorsque les binômes qui participent à la multiplication ont pour terme commun la variable

$x,$ Il existe une formule pour calculer rapidement cette opération binomiale :

$(x+a)(x+b) = x^2+(a+b)x+ab$

Ici, nous vous montrons un exercice résolu afin que vous puissiez voir comment appliquer cette formule :

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

binôme de Newton

Le binôme de Newton , également appelé théorème du binôme, est une formule utilisée pour calculer les puissances des binômes.

La formule mathématique du binôme de Newton est la suivante :

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

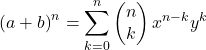
Ou équivalent:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Comme vous pouvez le voir, cette formule est un peu complexe à comprendre. C’est pourquoi nous avons fait les puissances des binômes du plus bas degré ci-dessous afin que vous puissiez mieux le comprendre :

Cette formule peut être un peu fastidieuse pour calculer des binômes au carré ou au cube, puisque, comme nous l’avons vu plus haut, il existe des formules plus simples. Cependant, le binôme de Newton est très utile pour trouver des puissances d’un degré supérieur, par exemple, il est largement utilisé pour déterminer un binôme à la quatrième.

Mais pour appliquer cette formule, il faut savoir calculer un nombre combinatoire, c’est-à-dire l’expression algébrique du type

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$ , calcul pas facile. 🔍 C’est pourquoi nous vous recommandons de chercher comment cela se fait dans notre moteur de recherche en haut à droite 🔎, vous trouverez notre article où nous vous expliquons étape par étape cette opération.