Identités notables (ou produits notables) -

Vous trouverez ici l’explication de la résolution de tous les types d’identités notables (ou de produits notables). Vous pourrez voir quelles sont les formules de toutes les identités notables, ainsi que des exemples et des exercices résolus étape par étape. De plus, nous allons vous montrer à quoi servent ces fameuses règles mathématiques.

👉👉 Ci-dessous nous expliquons chaque identité notable pas à pas, mais si vous préférez vous pouvez aller directement au tableau 😉 où toutes les formules sont résumées . 👈👈

Que sont les identités notables (ou produits notables) ?

Les identités remarquables , également appelées produits remarquables ou égalités remarquables , sont des règles mathématiques qui permettent de résoudre directement des opérations avec des polynômes.

Les formules d’identités notables les plus courantes sont le carré d’une somme , le carré d’une différence (ou soustraction) et la somme multipliée par la différence .

identités de produits ou égalités notables

Mais ci-dessous nous ne vous apprendrons pas seulement comment calculer ces produits notables, mais nous vous montrerons également tous les types d’identités notables qui existent.

Formules d’identités (ou produits) notables

Une fois que nous avons vu la définition des produits notables (ou des égalités notables), nous allons voir quelles sont les formules des identités notables. D’autre part, si vous êtes intéressé par les démos de formules, vous pouvez les afficher en cliquant sur les boutons “voir la démo de formule”.

carré d’une somme

Le carré d’une somme , ou somme au carré , est l’une des principales identités notables. Plus précisément, c’est un binôme à deux termes positifs à la puissance 2, c’est-à-dire que son expression algébrique est (a+b) ² .

Ainsi, la formule du carré d’une somme est :

Voir la démonstration de la formule

Si on part d’un binôme positif élevé au 2 :

$(a+b)^2$

Mathématiquement, le carré ci-dessus est équivalent au facteur

$(a+b)$ multiplié par lui-même :

$(a+b)^2=(a+b)\cdot (a+b)$

Donc, nous faisons la multiplication de polynômes en utilisant la propriété distributive :

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Sur les quatre termes obtenus,

$ab$ et $ba$ se ressemblent donc on peut les regrouper :

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Si bien que nous sommes déjà arrivés à l’expression de la formule d’une somme au carré, pour laquelle il est démontré :

$(a+b)^2= a^2+2ab+b^2$

Par curiosité, le développement de l’expression de ce type de produit remarquable est appelé un trinôme carré parfait.

De sorte que le carré d’une somme est égal au carré du premier terme, plus le double du produit du premier par le second, plus le carré du second.

Donc pour résoudre une somme au carré, il ne suffit pas d’élever chaque addition aux deux, mais, en plus, les deux additions doivent être multipliées entre elles et par 2. Il est important de s’en souvenir car une erreur très typique de ce type de produit Il est remarquable d’oublier ce terme.

Exemple:

Calculez l’identité notable suivante en appliquant sa formule correspondante :

$(x+5)^2$

Comme nous venons de le voir, la formule de l’égalité notable d’une somme au carré est :

$(a+b)^2=a^2+2ab+b^2$

Par conséquent, nous devons d’abord identifier les paramètres

$a$ et $b$ de la formule. Dans ce cas, $a$ représente le $x$ du binôme et $b$ correspond au numéro 5 :

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Donc, maintenant que nous connaissons les valeurs de

$a$ et de $b,$ on peut utiliser la formule d’un binôme positif au carré pour trouver le résultat :

carré d’une différence

Le carré d’une différence , ou différence au carré , est une autre des 3 identités notables les plus utilisées. En particulier, il correspond à un binôme formé par un terme positif et un autre terme négatif élevé au 2, c’est-à-dire que son expression algébrique est (ab) ² .

Ainsi, la formule du carré d’une différence (ou carré d’une soustraction) est la suivante :

Voir la démo de la formule

A partir de l’expression du binôme d’une soustraction élevée au carré :

$(a-b)^2$

Évidemment, la puissance précédente est égale au produit du facteur

$(a-b)$ multiplié par lui-même :

$(a-b)^2= (a-b)\cdot (a-b)$

Maintenant, nous multiplions les deux parenthèses en appliquant la propriété distributive :

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Il suffit donc de regrouper les termes similaires pour finir de vérifier la formule :

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Ensuite, la formule du carré d’une différence est prouvée mathématiquement :

$(a-b)^2=a^2-2ab+b^2$

De sorte que le carré d’une différence est égal au carré du premier terme, moins le double du produit du premier par le second, plus le carré du second.

Comme pour l’égalité remarquable de la somme aux carrés, il ne faut pas oublier de mettre le moyen terme de la formule, puisque l’équation suivante est incorrecte :

Exemple:

Résolvez l’égalité notable suivante d’une différence au carré :

$(x-3)^2$

C’est le produit notable d’une soustraction au carré, il faut donc appliquer sa formule correspondante :

$(a-b)^2=a^2-2ab+b^2$

Ensuite, il faut identifier quelles sont les valeurs des inconnues

$a$ et $b$ de la formule. Dans ce cas, $a$ est la variable $x$ et $b$ correspond au numéro 3 :

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Notez que le signe négatif ne fait pas partie du paramètre

$b,$ mais il faut toujours prendre le nombre sans le signe pour appliquer correctement cette formule.

Nous connaissons donc déjà les valeurs de

$a$ et de $b$ , il suffit donc de substituer ces valeurs dans la formule pour résoudre l’identité notable :

exemples et exercices résolus pas à pas d'égalités notables

somme par différence

Le produit d’une somme par une différence est l’une des 3 identités notables les plus utilisées. Comme son nom l’indique, c’est un binôme positif multiplié par son binôme conjugué (même binôme mais avec le signe intermédiaire changé), c’est-à-dire que l’expression algébrique de ce type de produit remarquable est (a+b)·(ab ) .

La formule de l’identité remarquable du produit d’une somme par une différence est la suivante :

identités, produits et égalités notables des lycées 2, 3 et 4 qui

Voir la démonstration de la formule

Partant du produit d’une somme par une soustraction de deux termes quelconques :

$(a+b)\cdot (a-b)$

Pour démontrer la formule, nous devons simplement multiplier la première parenthèse par la deuxième parenthèse en utilisant la propriété distributive :

$\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}$

Maintenant, nous regroupons des termes similaires :

$a^2 -ab+ba-b^2=a^2-b^2$

Et nous sommes ainsi parvenus à l’expression d’une égalité remarquable. Ainsi la formule de ce type d’identité remarquable est démontrée :

$(a+b)\cdot (a-b) =a^2-b^2$

Ainsi, le produit de la somme par la différence de deux quantités est égal à la différence des carrés de ces quantités. Ou en d’autres termes, multiplier la somme de deux termes différents par la soustraction de ces deux mêmes termes équivaut à mettre au carré chacun des 2 termes et à les soustraire.

Exemple:

Trouver, à l’aide de la formule correspondante, le produit notable suivant de la somme par la différence de deux termes différents :

$(x+2)\cdot (x-2)$

Comme nous l’avons vu plus haut, la formule de l’égalité notable d’une somme multipliée par une différence est la suivante :

$(a+b)\cdot (a-b) =a^2-b^2$

Tout d’abord, ce que nous devons faire est d’identifier les valeurs des lettres

$a$ et $b$ de la formule. Dans ce cas $a$ correspond à la variable $x$ et $b$ correspond au numéro 2.

$\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Et quand on sait déjà quelles valeurs prennent les paramètres

$a$ et $b,$ On applique la formule du produit de la somme par la différence :

carré d’un trinôme

Le carré d’un trinôme (polynôme formé de 3 termes) est égal au carré du premier terme, plus le carré du deuxième terme, plus le carré du troisième terme, plus deux fois le premier par le second, plus deux fois le premier par le troisième, plus deux fois le second pour le troisième.

Quelles sont les formules de toutes les identités, produits ou égalités notables ?

Voir la démo de la formule

A partir de n’importe quel trinôme élevé au carré :

$(a+b+c)^2$

Le carré ci-dessus peut être factorisé dans le trinôme multiplié par lui-même :

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Maintenant, nous résolvons la multiplication polynomiale :

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

Et enfin, nous regroupons des termes similaires :

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

De cette façon, nous sommes déjà arrivés à l’expression de la formule, donc la formule du carré d’un trinôme est démontrée :

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Exemple:

Trouver l’égalité notable suivante :

$\left(x^2+x+3\right)^2$

La formule du carré d’un trinôme est :

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Comme dans toutes les égalités notables, il faut d’abord identifier les valeurs des inconnues dans la formule. Dans cet exercice

$a$ est $x^2,$ le coefficient $b$ correspond à la $x,$ et $c$ est le terme indépendant 3 :

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

Et quand on connaît déjà les valeurs, il suffit de substituer ces valeurs dans la formule et de faire les calculs :

calculateur d'identités, de produits et d'égalités notables

Identités (ou produits) notables au cube

Nous venons d’étudier toutes les identités notables au carré, c’est-à-dire tous les types d’identités notables qui sont formés par des puissances élevées à 2. Eh bien, nous allons maintenant analyser les identités notables au cube. Bien sûr, les formules d’identités au cube sont un peu plus compliquées, mais elles sont aussi très utiles.

cube d’une somme

Le produit notable du cube d’une somme est un binôme (polynôme avec seulement deux monômes) à la puissance 3 dont les deux éléments sont positifs. Par conséquent, algébriquement, le cube d’une somme s’exprime par (a+b) ³ .

La formule de l’égalité notable du cube d’une somme est :

Quels sont tous les produits, identités ou égalités notables ?

Voir la démonstration de la formule

Partant d’un binôme positif élevé au cube :

$(a+b)^3$

La puissance ci-dessus peut être factorisée dans le produit du facteur

$(a+b)$ par son carré :

$(a+b)^3=(a+b)\cdot (a+b)^2$

De même, comme nous l’avons vu dans les égalités au carré notables, le binôme

$(a+b)$ Il peut être résolu avec la formule du carré d’une somme :

$(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)$

Puis on multiplie les deux polynômes ensemble :

$\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}$

Pour finir, nous n’avons qu’à regrouper les termes similaires :

$a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3$

Et ainsi se vérifie la formule de l’identité notable d’un binôme somme élevé au cube :

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Bref, une somme élevée à 3 est égale au cube du premier, plus le triple du carré du premier par le second, plus le triple du premier par le carré du second, plus le cube du second.

Exemple:

Résolvez l’identité notable suivante d’une somme au cube en utilisant sa formule correspondante :

$(x+2)^3$

Dans ce problème nous avons un binôme à la puissance 3 dont les deux termes sont positifs. Il faut donc utiliser la formule d’une somme élevée au cube :

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Il faut maintenant trouver la valeur des paramètres

$a$ et $b$ de la formule. Dans ce cas, $a$ correspond à la variable $x$ et $b$ est le numéro 2.

$\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Avec lequel nous calculons le produit notable en remplaçant les valeurs de

$a$ et de $b$ dans la formule :

10 exemples de produits ou d'identités notables

cube d’une différence

Le cube d’une différence , ou cube d’une soustraction , est un binôme à la puissance 3 qui a un terme avec un signe négatif. Ainsi, l’expression mathématique de ce type de produit remarquable est (ab) ³ .

La formule du cube d’une différence (ou soustraction) est :

identités, produits ou égalités cubiques remarquables

Voir la démonstration de la formule

Évidemment, la preuve de cette formule est très similaire à celle du produit notable d’une somme au cube. Mais dans ce cas, nous partons d’un binôme au cube négatif :

$(a-b)^3$

Clairement, la potentialisation précédente peut être décomposée en produit du facteur

$(a-b)$ multiplié par son carré :

$(a-b)^3=(a-b)\cdot (a-b)^2$

Alors, comme nous l’avons étudié dans les identités au carré notables, le binôme

$(a-b)$ Il peut être calculé avec la formule du carré d’une différence :

$(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)$

On fait maintenant le produit des deux polynômes :

$\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}$

Et la dernière étape consiste à regrouper les termes similaires :

$a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3$

Ainsi la formule de l’identité notable d’un binôme soustrait élevé au cube est vérifiée :

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

Donc, une différence (ou une soustraction) élevée à trois équivaut au cube du premier, moins le triple du carré du premier par le second, plus le triple du premier par le carré du second, moins le cube de la seconde.

Exemple:

Calculez le binôme au cube suivant (différence) à l’aide de sa formule correspondante :

$(3x-2)^3$

Dans cet exercice, nous avons un binôme avec un élément positif et un élément négatif. Il faut donc utiliser la formule d’une différence élevée au cube :

$(a-b)^3 = a^3-3a^2b+3ab^2 -b^3$

D’abord, comme toujours, nous identifions la valeur des inconnues

$a$ et $b$ de la formule. Dans ce cas $a$ représente le monôme $3x$ et $b$ est le terme indépendant du binôme, soit 2.

$\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}$

Notez que le paramètre

$b$ est simplement égal à 2, sans le signe négatif du nombre. Il est important de garder cela à l’esprit pour bien appliquer la formule.

Enfin, on retrouve l’identité remarquable en mettant les valeurs de

$a$ et de $b$ dans la formule :

développer des identités, des produits et des égalités remarquables

Tableau récapitulatif des identités notables

En résumé, nous avons fait un tableau avec toutes les identités (ou produits) notables que nous avons vues, il vous sera donc plus facile de les étudier. 😉

formules d'identités ou d'égalités de produits notables

Exercices résolus d’identités (ou de produits) notables

Afin que vous finissiez de comprendre la notion d’identités remarquables, aussi appelées produits remarquables ou égalités remarquables, nous vous avons préparé plusieurs exercices résolus étape par étape. Vous pouvez essayer de les faire et ensuite vérifier si vous avez bien réussi avec les solutions des exercices.

⬇⬇ N’oubliez pas que vous pouvez nous poser toutes vos questions ci-dessous dans les commentaires ! ⬇⬇

Exercice 1

Développez les identités notables suivantes (carrés de somme) :

$\text{A)} \ (x+3)^2$

$\text{B)} \ (6x+2)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

voir solution

Toutes les identités notables dans le problème sont des sommes au carré, donc dans ce cas nous devons toujours appliquer la même formule :

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Exercice 2

Développer les produits notables suivants (différences au carré) :

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

voir solution

Tous les produits notables de cet exercice sont des soustractions élevées au carré, nous n’avons donc qu’à appliquer une seule formule :

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

Exercice 3

Développez les égalités notables suivantes (produits de sommes par différences) :

$\text{A)} \ (x+5)(x-5)$

$\text{B)} \ (2x+6)(2x-6)$

$\text{C)} \ (x+7)(x-7)$

$\text{D)} \ (x-4y)(x+4y)$

voir solution

Puisque toutes les égalités notables dans cet exercice sont des multiplications de sommes par des différences, elles sont toutes résolues avec la même formule :

$(a+b)\cdot (a-b) =a^2-b^2$

$\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}$

$\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}$

$\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}$

$\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}$

Exercice 4

Résolvez toutes les identités notables suivantes :

$\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)$

$\text{B)} \ \left(4x^2+2y^3\right)^2$

$\text{C)} \ \left(6x^3-4y^4\right)^2$

$\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)$

$\text{E)} \ \left(5x^2-9x\right)^2$

voir solution

$\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

$\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}$

$\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}$

Exercice 5

Calculez les produits notables suivants :

$\text{A)} \ (x+4)^3$

$\text{B)} \ \left(x^2-5\right)^3$

$\text{C)} \ \left(2x-1\right)^3$

$\text{D)} \ (5x+2)^3$

voir solution

Pour trouver tous les produits notables du problème il faut appliquer les formules d’une somme et d’une différence au cube selon les cas :

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

$\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}$

Exercice 6

Résolvez les égalités notables suivantes :

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

voir solution

Pour résoudre toutes ces identités notables, nous devons utiliser la formule du carré d’un trinôme, qui est :

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Exercice 7

Calculez les identités notables suivantes avec racines et fractions (difficulté élevée) :

$\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

$\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)$

voir solution

La section A) consiste en une soustraction élevée au carré, donc pour la résoudre, sa formule correspondante doit être appliquée et, de plus, il faut se rappeler que si une racine est élevée au carré, elle est simplifiée :

$\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

La section B) traite d’une addition par une soustraction et les monômes ont des coefficients fractionnaires, avec lesquels il faut déterminer ce produit notable au moyen de la formule d’une addition par une soustraction et des propriétés des fractions :

$\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}$

L’égalité notable de la section C) est une somme élevée à 2 et, de même, est composée de fractions. Par conséquent, pour le calculer, nous devons utiliser la formule d’une somme au carré plus les propriétés des fractions :

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

La dernière identité notable traite d’une somme multipliée par une différence avec des coefficients irrationnels, nous appliquons donc la formule pour une somme multipliée par une différence, puis nous simplifions les racines au carré :

$\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}$

Autres types d’identité notables

Toutes les identités notables dont nous avons discuté ci-dessus sont les plus couramment utilisées. Cependant, en mathématiques, il existe d’autres types de produits notables qu’il est également intéressant de connaître, car ils sont utilisés à des fins différentes.

somme de cubes

La somme des cubes correspond à un binôme dont les deux termes sont positifs et, de plus, ses racines cubiques sont exactes. Par conséquent, l’expression algébrique d’une somme de cubes est a ³ +b ³ .

identités, produits ou égalités notables résolus

La formule de ce produit notable est utilisée pour factoriser un polynôme, c’est-à-dire qu’à travers la formule on transforme un polynôme en un produit d’un binôme par un trinôme.

Pour que vous puissiez voir comment c’est fait, voici un exemple d’application de cette identité remarquable :

$x^3+8$

En effet, l’expression précédente consiste en une addition de cubes car la racine cubique du monôme

$x^3$ est exact (ne donne pas de nombre décimal) et le nombre 8 aussi :

$\sqrt[3]{x^3} = x$

$\sqrt[3]{8} = 2$

$x^3+8=x^3+2^3$

Par conséquent, nous pouvons utiliser la formule de la somme des cubes parfaits pour transformer l’expression cubique en un produit d’un binôme par un trinôme :

$a^3+b^3 = (a+b)(a^2-ab+b^2)$

$\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}$

différence de cubes

La différence (ou soustraction) de cubes est un binôme composé d’un terme positif et d’un terme négatif dont les racines cubiques sont exactes. Autrement dit, une différence de cubes s’exprime sous la forme a ³ -b ³ .

Exercices résolus de factorisation de polynômes avec des identités notables

Faisons un exemple pour que vous puissiez voir comment ce type d’identité remarquable est résolu :

$x^3-27$

C’est une différence de cubes car à la fois la racine cubique du monôme

$x^3$ comme 27 sont exacts:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{27} = 3$

$x^3-27=x^3-3^3$

Vous pouvez donc utiliser la formule de la différence des cubes parfaits pour factoriser le binôme :

$a^3-b^3 = (a-b)(a^2+ab+b^2)$

$\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}$

Produit de binômes avec un terme commun

Ce produit notable est utilisé pour convertir un produit de deux binômes qui ont un terme commun en un polynôme du second degré.

identités, produits ou égalités remarquables pdf

Voici un exemple élaboré de ce type de produit remarquable :

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

plus d’identités

Bien que les identités notables soient les plus célèbres car elles sont les plus courantes, il convient de noter qu’il existe également plus d’identités avec d’autres noms. Voici une liste d’autres identités moins connues au cas où vous seriez curieux :

Identités de Lagrange :

$(a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2$
$(a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2$

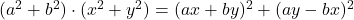
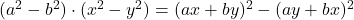
Identités Legendre :

$(a+b)^2+(a-b)^2=2(a^2+b^2)$
$(a+b)^2-(a-b)^2=4ab$
$(a+b)^4-(a-b)^4=8ab(a^2+b^2)$

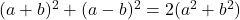
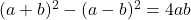
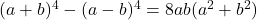
L’identité d’Argand :

$(x^2+x+1)(x^2-x+1) = x^4+x^2+1$

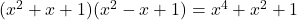
Identités gaussiennes :

$a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)$
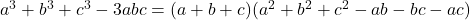
$a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]$

Applications d’identité notables

Si vous êtes arrivé jusqu’ici, cela signifie que vous savez déjà comment faire des calculs avec des identités notables. Brillant! Mais vraiment… à quoi servent les identités notables ? Et quand les identités notables sont-elles utilisées ?

Comme nous l’avons vu tout au long de cet article, l’utilité principale des identités notables est de simplifier les calculs. C’est-à-dire que grâce à des produits remarquables on peut résoudre directement certaines puissances de polynômes complexes sans avoir à effectuer des opérations difficiles.

Mais les égalités notables ont également d’autres fonctions, telles que la factorisation de polynômes et la complétion de carrés. Ensuite nous verrons en quoi consiste chacune de ces applications.

Factorisation de polynômes

Certains types très spécifiques de polynômes peuvent être factorisés avec des identités notables. Par exemple, si l’on trouve un polynôme composé de deux termes qui sont des carrés parfaits (leurs racines carrées sont exactes), on peut le factoriser à l’aide de la formule d’égalité remarquable du produit d’une somme par une différence :

$a^2-b^2 =(a+b)(a-b)$

$x^2-9 =(x+3)(x-3)$

De même, les trinômes qui respectent les identités notables du carré d’une addition ou d’une soustraction peuvent être factorisés :

$a^2+2ab+b^2=(a+b)^2$

$x^2+4x+4=(x+2)^2$

$a^2-2ab+b^2=(a-b)^2$

$x^2-10x+25=(x-5)^2$

De même, une fois qu’un polynôme a été factorisé, les racines (ou zéros) de ce polynôme peuvent être trouvées. Même ainsi, ce concept est un peu plus compliqué à comprendre, donc si vous êtes plus intéressé, nous vous recommandons de rechercher l’explication dans le moteur de recherche sur notre site Web (en haut à droite), car nous avons un article entier l’expliquant.

achèvement carré

La complétion des carrés est une procédure mathématique utilisée pour convertir un trinôme quadratique en la somme d’un carré plus (ou moins) un nombre.

Etant donné n’importe quel trinôme :

$ax^2+bx+c$

Ensuite, le trinôme peut être transformé en l’expression suivante :

$a(x+h)^2+k$

où les paramètres

$h$ et $k$ sont calculés avec les formules suivantes :

$h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2$

Même si cela ne vous semble pas, ces deux formules sont déduites d’identités notables. Ainsi, grâce aux produits remarquables, les carrés peuvent être complétés.

A titre d’exemple, nous allons appliquer cette procédure au trinôme suivant :

$2x^2+4x+3$

Nous calculons les paramètres

$h$ et $k:$

$h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1$

$k=c-ah^2 = 3-2\cdot 1^2 = 1$

Et, par conséquent, le polynôme reste :

$2(x+1)^2+1$

Que sont les identités notables (ou produits notables) ?

Formules d’identités (ou produits) notables

carré d’une somme

Exemple:

carré d’une différence

Exemple:

somme par différence

Exemple:

carré d’un trinôme

Exemple:

Identités (ou produits) notables au cube

cube d’une somme

Exemple:

cube d’une différence

Exemple:

Tableau récapitulatif des identités notables

Exercices résolus d’identités (ou de produits) notables

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Autres types d’identité notables

somme de cubes

différence de cubes

Produit de binômes avec un terme commun

plus d’identités

Applications d’identité notables

Factorisation de polynômes

achèvement carré

Leave a Comment Cancel Reply