Sur cette page vous découvrirez comment diviser des polynômes, aussi bien la division d’un polynôme par un monôme que la division d’un polynôme par un autre polynôme. Vous pourrez également voir des exemples de divisions de polynômes et vous entraîner avec des exercices résolus étape par étape. Et en plus, vous trouverez les propriétés de cette opération polynomiale.
Division polynomiale (ou polynomiale)
Avant de voir exactement comment deux polynômes sont divisés, nous allons revoir brièvement les concepts de division polynomiale, afin qu’il soit ensuite plus facile de comprendre la méthode que nous allons utiliser.
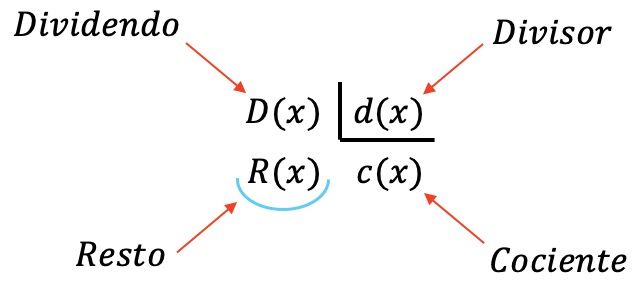
Quatre polynômes sont impliqués dans une division polynomiale :
- Dividende : le polynôme divisé.
- Diviseur : le polynôme qui divise le dividende.
- Quotient : résultat de la division du dividende par le diviseur.
- Reste (ou résidu) : le polynôme restant lors de la division entre les deux polynômes.
D’autre part, il faut aussi savoir qu’il existe deux types de division entre polynômes :
- Division exacte de polynômes : une division entre polynômes est exacte lorsque le reste est nul. Dans ce cas, le polynôme de dividende est égal au diviseur multiplié par le quotient.
De plus, dans ce cas, le dividende
est un multiple du diviseur
et le quotient
De même, le polynôme diviseur et le polynôme quotient sont tous deux des diviseurs du dividende.
- Division entière de polynômes : dans une division entière (ou inexacte) de polynômes le reste est différent de zéro (0). Alors, la propriété fondamentale de la division polynomiale est satisfaite :
Maintenant que nous avons vu ce qu’est la division de polynômes, voyons comment diviser les polynômes les uns par les autres. Plus précisément, nous expliquerons d’abord la division entre un polynôme et un monôme puis la division entre 2 polynômes.
Division d’un polynôme par un monôme
Avant de voir comment diviser un polynôme par un monôme, rappelons d’abord comment les monômes sont divisés entre eux, puisqu’il est nécessaire de le connaître pour pouvoir faire ce type d’opération polynomiale.
La division de deux monômes consiste à diviser leurs coefficients entre eux et leurs parties littérales entre eux, c’est-à-dire que les coefficients des monômes sont divisés et que les exposants des variables qui ont la même base sont soustraits. Regardez l’exemple suivant :
Voyons maintenant en quoi consiste la division d’un polynôme par un monôme :
En mathématiques, pour résoudre la division d’un polynôme par un monôme, chaque terme du polynôme est divisé par le monôme.
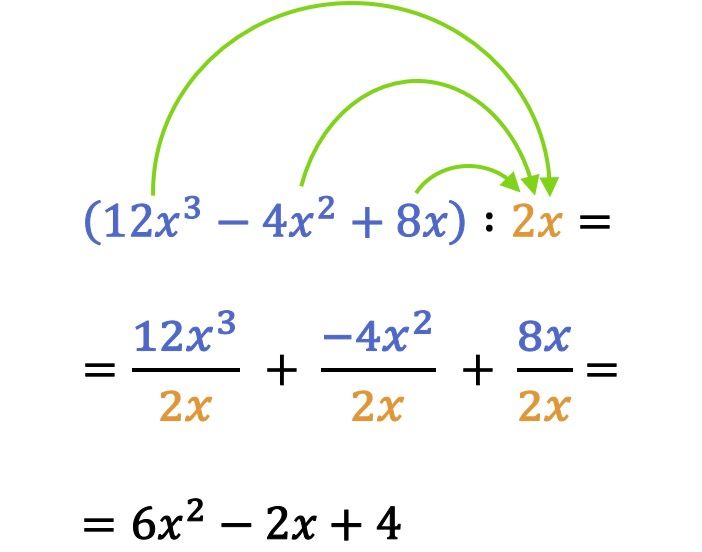
Remarquez dans l’exemple de la division précédente que lorsqu’on divise des monômes ou des polynômes il faut aussi tenir compte de la règle des signes. En fait, une erreur très courante dans les divisions entre polynômes et monômes est de se tromper sur le signe d’un terme.
Division d’un polynôme par un autre polynôme
Pour diviser deux polynômes, il faut suivre une procédure, voyons donc à quoi ressemble la méthode de division de polynômes, également appelée division longue de polynômes, en résolvant un exemple étape par étape :
- Calculer le résultat de la division du polynôme
entre le polynôme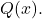
Étant les deux polynômes :
La première chose à faire est de placer les polynômes sous forme de division. A gauche on écrit le numérateur de la fraction (polynôme dividende) et à droite on met le dénominateur de la fraction (polynôme diviseur) :
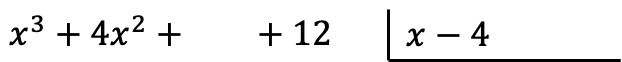
Attention : Si un polynôme n’a pas de monôme d’un certain degré, nous devons laisser un espace à sa place. Par exemple, le polynôme
Il n’y a pas de terme de première année, il y a donc un espace vide à la place.
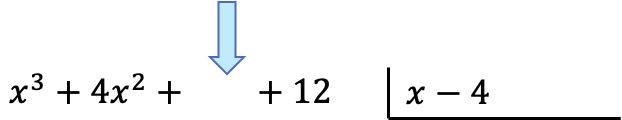
Une fois que nous avons mis les polynômes en place, nous allons trouver le quotient. Et pour trouver le premier terme du quotient il faut diviser le premier terme du dividende par le premier terme du diviseur :
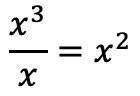
Et on met le résultat de la division à la place du quotient :
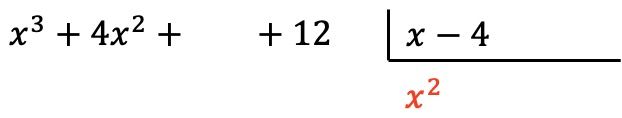
Maintenant on multiplie le terme trouvé par chaque élément du diviseur, et on met chaque résultat en dessous du dividende dans sa colonne correspondante , en changeant son signe :
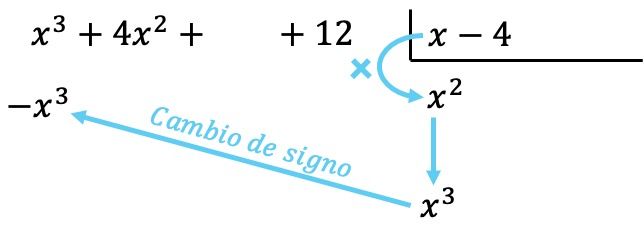
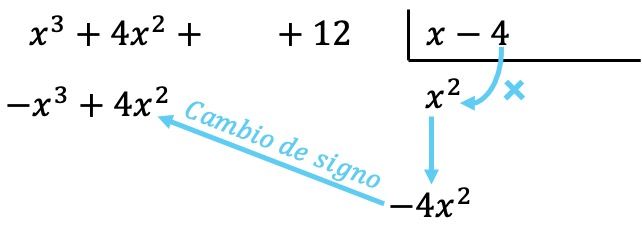
Comme dans toutes les opérations avec des polynômes, il est important d’ordonner les polynômes du degré le plus élevé au degré le plus bas afin que tous les termes de même degré se trouvent dans la même colonne.
Une fois que nous avons placé les résultats des multiplications avec le signe opposé, nous devons ajouter les termes alignés verticalement :
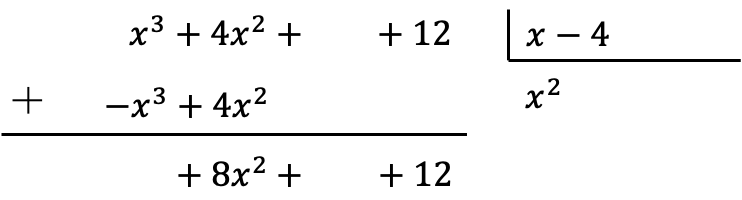
Notez qu’en faisant cette somme, le coefficient ayant le degré le plus élevé s’annule et, par conséquent, nous avons un terme de moins dans le dividende.
Nous devons maintenant répéter la même procédure jusqu’à ce que le polynôme dividende soit d’un degré inférieur au polynôme diviseur.
On divise donc le premier terme du dividende par le premier terme du diviseur :
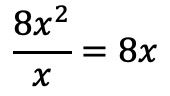
On place le résultat dans le quotient :
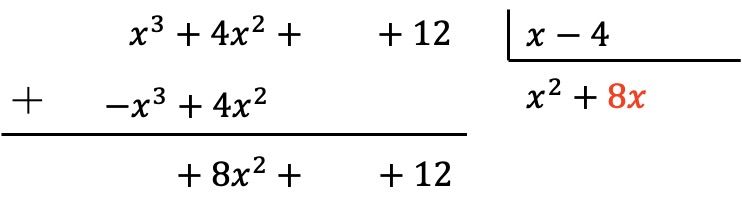
Comme précédemment, on multiplie le nouveau terme du quotient par chaque élément du diviseur et on met les résultats de signe opposé dans les colonnes correspondantes du dividende :
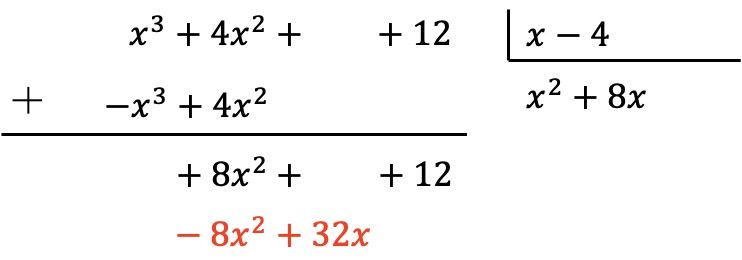
Et on ajoute verticalement :
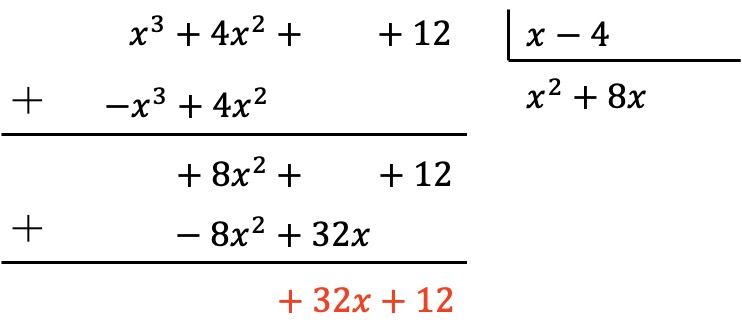
Le polynôme dividende n’est toujours pas d’un degré inférieur au polynôme diviseur, nous devons donc continuer à faire le même processus.
Donc d’abord on divise le premier terme du dividende par le premier terme du diviseur, ensuite on multiplie le résultat par chaque terme du diviseur, puis on met les résultats modifiés en signe dans le dividende et, enfin, on additionne verticalement :
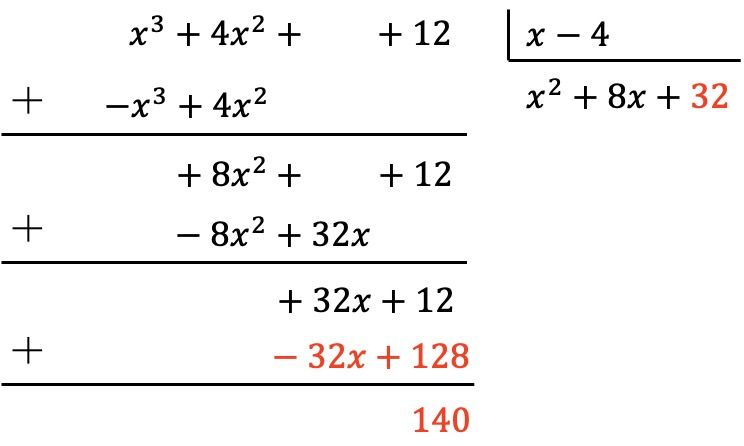
Nous avons donc déjà obtenu que le polynôme du dividende est de degré inférieur au degré du diviseur, car le dividende est de degré 0 et le diviseur de degré 1. Par conséquent, la division est terminée.
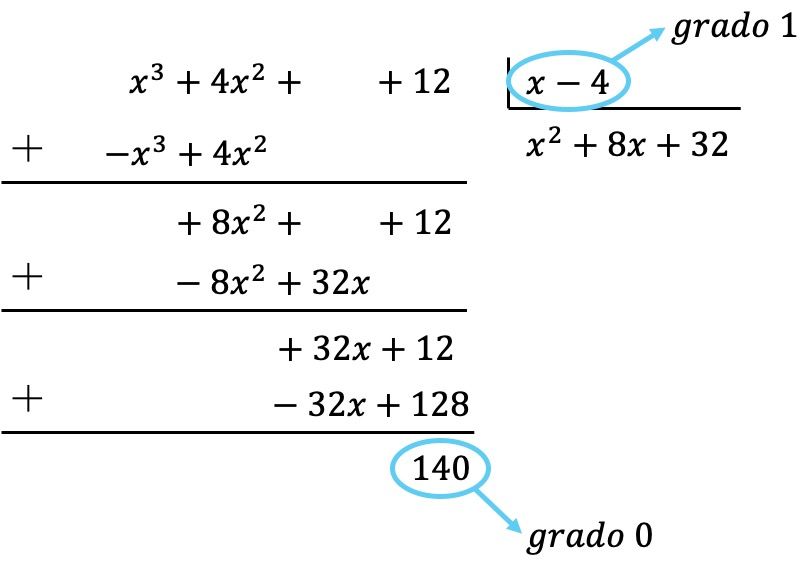
Le résultat de la division est donc :
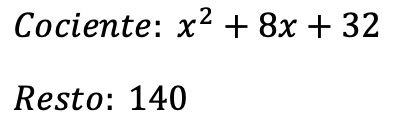
D’autre part, nous pouvons vérifier que nous avons effectué correctement la division polynomiale en nous basant sur la condition fondamentale de la division des polynômes :
✅
L’équation est satisfaite, la division polynomiale a donc été effectuée correctement.
Pour que nous ayons fini de diviser les polynômes, nous espérons avoir pu vous aider avec cette explication. Qu’avez-vous pensé de la méthode de division des polynômes ? As-tu un doute? Tu aimes? Ou préféreriez-vous que les divisions polynomiales n’existent pas ? 😂 On vous lit dans les commentaires ! 👇👇👇
Propriétés de division des polynômes
Toute division de polynômes répond aux caractéristiques suivantes :
✓ Le degré du polynôme dividende doit toujours être supérieur au degré du polynôme diviseur.
✓ Le degré du polynôme de dividende est équivalent à la somme des degrés du diviseur et du quotient.
✓ Le degré du reste est toujours inférieur au degré du diviseur (et donc aussi du dividende).
✓ Le dividende est égal au produit du diviseur par le quotient plus le reste. Cette condition est également remplie dans la division des nombres.
Exercices résolus sur la division des polynômes
Exercice 1
Déterminer le résultat de la division suivante d’un polynôme par un monôme :
Pour diviser un polynôme par un monôme il faut résoudre la division de chaque terme du polynôme par ledit monôme :
![\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffa558b26adc36e2ac45a842a6cf33df_l3.png "Rendered by QuickLaTeX.com")
N’oubliez pas que lors de la division entre les monômes, les coefficients sont divisés entre eux et les exposants des puissances dont la base est la même sont soustraits.
Exercice 2
Calculez la division suivante d’un polynôme par un monôme :
Pour diviser un polynôme par un monôme il faut diviser chaque terme du polynôme par ledit monôme :
![\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868da1546d3e4d33e8226774020cbb2d_l3.png "Rendered by QuickLaTeX.com")
N’oubliez pas que dans la division monôme, les coefficients sont divisés entre eux et les exposants des puissances dont la base est équivalente sont soustraits.
Exercice 3
Résolvez la division suivante d’un polynôme par un monôme :
Pour diviser un polynôme par un monôme il faut résoudre la division de chaque terme du polynôme par ledit monôme :
![\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8d5fe46b397f2f531a865e7cb0df3cf_l3.png "Rendered by QuickLaTeX.com")
Gardez à l’esprit que le monôme diviseur est négatif et que, par conséquent, les signes de toutes les divisions changent.
Exercice 4
Effectuez la division suivante des polynômes :
Pour diviser des polynômes il faut appliquer la méthode expliquée ci-dessus :
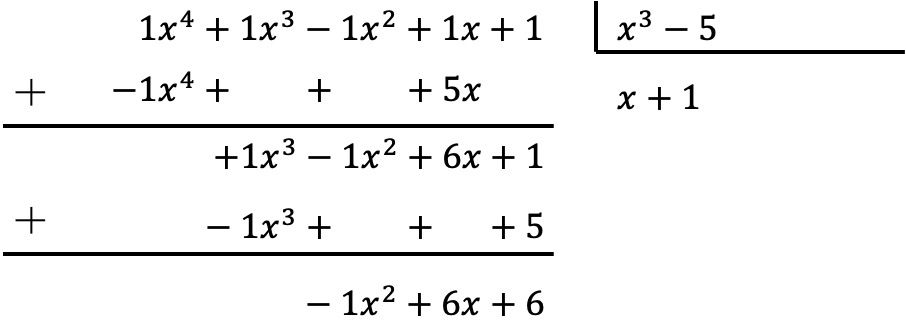
Le résultat de la division entre les deux polynômes est donc :
Quotient:
Repos:
Exercice 5
Calculez la division suivante de polynômes :
Pour résoudre la division du polynôme par le binôme il faut appliquer la méthode que nous avons vue ci-dessus :
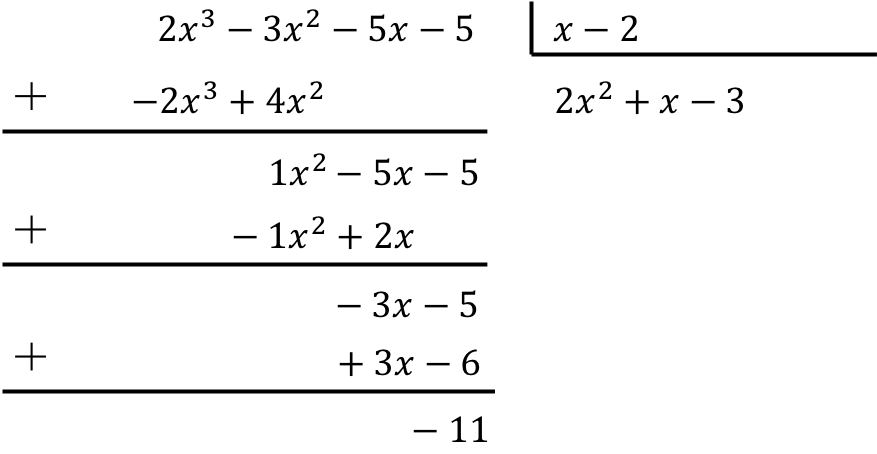
Le résultat de la division polynomiale est donc :
Quotient:
Repos:
Exercice 6
Résolvez la division de polynômes suivante :
Pour calculer la division des polynômes, nous devons appliquer la méthode expliquée :
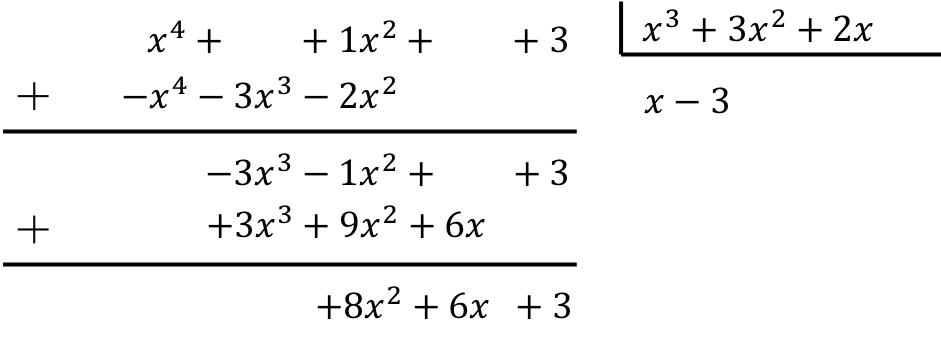
Le résultat de la division entre les deux polynômes est donc :
Quotient:
Repos:
Exercice 7
Trouvez le résultat de la division suivante entre 2 polynômes :
Pour calculer la division du polynôme par le trinôme il faut appliquer la méthode expliquée :
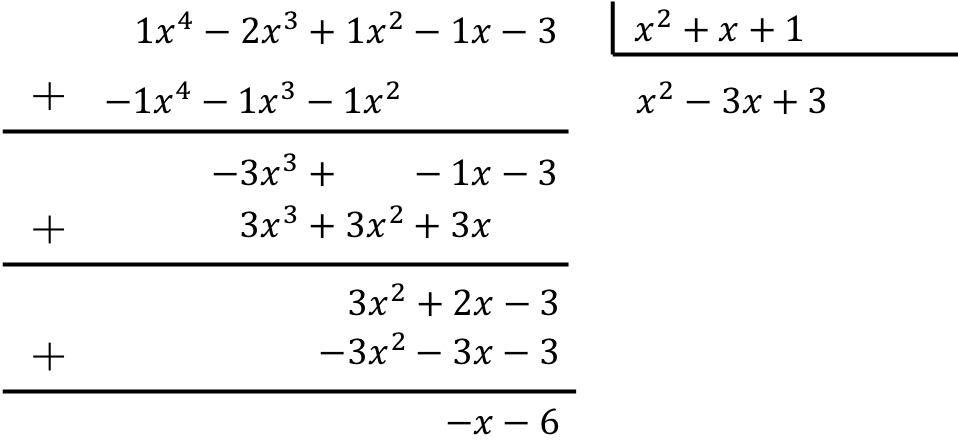
Le résultat de la division entre les deux polynômes est donc :
Quotient:
Repos:
👉👉👉Si vous êtes arrivé jusqu’ici, cela signifie que vous savez déjà comment les polynômes sont divisés. Brillant! Maintenant que vous maîtrisez les divisions de polynômes, sachez qu’il existe une méthode qui permet de résoudre certaines divisions entre polynômes beaucoup plus rapidement . Il s’agit d’ une division synthétique ou règle de Ruffini , vous pouvez voir comment cette astuce est appliquée et quand elle peut être utilisée en cliquant sur le lien.😉
