Vous trouverez ici l’explication de ce qu’elles sont et comment on les appelle toutes les parties d’un polynôme (degré, variables, terme indépendant,…). De plus, vous pourrez voir plusieurs exemples et pratiquer avec des exercices résolus des parties d’un polynôme.
Mais avant de voir ce que sont toutes les parties d’un polynôme, passons rapidement en revue sa définition mathématique afin de bien comprendre le concept : un polynôme est une expression algébrique formée par l’addition ou la soustraction de monômes de degrés différents.
Quelles sont les parties d’un polynôme ?
Les parties d’un polynôme sont :
- Termes : chaque monôme faisant partie du polynôme.
- Coefficients : les nombres qui accompagnent chaque terme du polynôme.
- Degré : Le plus grand exposant auquel la variable du polynôme est élevée.
- Variable : est la lettre que possède le polynôme.
- Terme principal : est le terme de plus haut degré du polynôme.
- Terme indépendant : terme du polynôme qui ne contient pas de variable.
- Coefficient dominant : coefficient du terme dominant du polynôme.
Lorsque le polynôme n’a qu’une seule variable, son degré est égal au plus grand exposant de ses termes. Cependant, si le polynôme a deux variables ou plus, il est plus difficile de connaître son degré puisqu’il faut faire une opération. Découvrez comment cela se fait en cliquant sur le lien suivant du degré d’un polynôme de deux variables (ou plus).
Comment identifier les parties d’un polynôme
Les parties ou éléments d’un polynôme peuvent être facilement trouvés visuellement. Voyez comment cela se fait dans le schéma suivant:
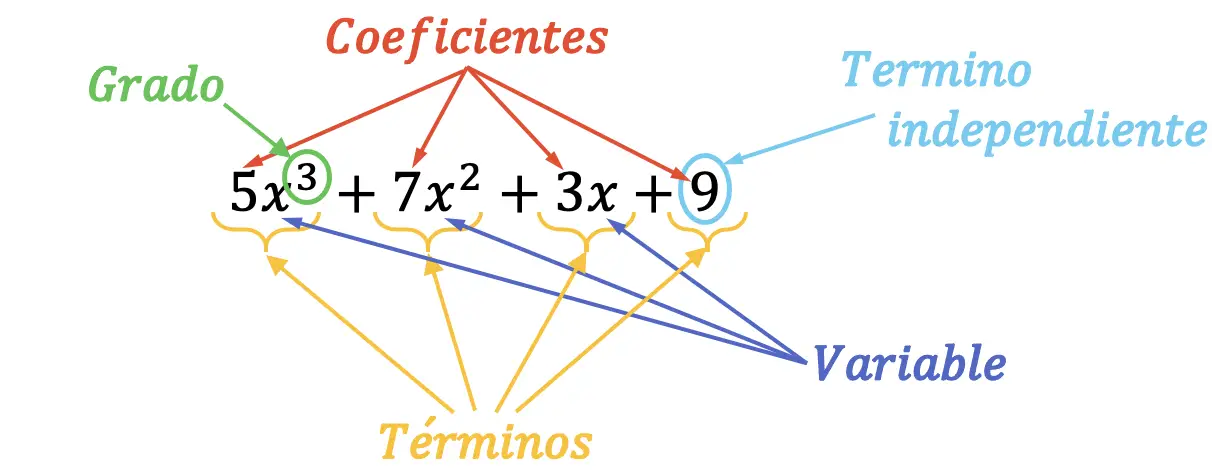
Le polynôme précédent, qui est du troisième degré, a toutes ses parties marquées. De plus, le terme principal dudit polynôme est d’environ 5x 3 , car c’est le monôme de degré le plus élevé. De même, le coefficient dominant du polynôme est 5, puisqu’il s’agit du coefficient du terme dominant.
Dans ce cas, le polynôme a une seule variable et n’a donc qu’un seul type de degré. Mais il faut savoir que lorsque le polynôme est multivariable, il faut faire la différence entre le degré absolu et le degré relatif d’une variable. Vous pouvez voir en quoi consiste chacun d’eux dans le lien que je vous ai laissé ci-dessus ⬆⬆ ( degré d’un polynôme de deux variables ).
Exemples de parties d’un polynôme
Pour finir de comprendre la signification des parties d’un polynôme et la fonction qu’elles remplissent, nous allons voir quelques exemples de détermination des parties de tout type de polynôme :
Exemple 1
Identifiez les parties du polynôme suivant du second degré (de degré 2) :
![]()
- Termes : 4x 2 , -8x, 1
- Coefficients : 4, -8, 1
- 2e année
- Variable : x
- Terme principal : 4x 2
- Mandat indépendant : 1
- Coefficient directeur : 4
D’autre part, il convient de noter que le polynôme dans cet exemple est appelé un trinôme . Vous pouvez voir en quoi consiste ce type de polynôme dans des exemples de trinômes . En outre, vous pouvez également être intéressé par un autre type de polynôme appelé binôme (il est plus facile de faire certaines opérations avec), vous pouvez voir ce qu’il a de spécial dans des exemples de binômes .
Exemple 2
Trouver les parties du polynôme suivant :
![]()
- Termes : y 3 , 9y 2 , -5y, 3
- Coefficients : 1, 9, -5, 3
- 3e année
- variables : et
- Terme principal : et 3
- Mandat indépendant : 3
- Coefficient directeur : 1
Comme vous pouvez le voir dans cet exemple, lorsqu’un monôme n’a pas de nombre devant lui, cela signifie que son coefficient est l’unité. Donc le coefficient directeur de ce polynôme est égal à 1.
Exercices résolus des parties d’un polynôme
Pour vous aider à retenir les noms de toutes les parties d’un polynôme, nous vous avons préparé plusieurs exercices résolus. Vous pouvez nous poser toutes vos questions à leur sujet dans les commentaires. ⬇⬇
Exercice 1
Trouver toutes les parties du polynôme suivant :
![]()
Le polynôme de cet exercice n’a pas de terme indépendant puisque tous les termes sont formés par au moins une variable (ou lettre).
Termes : 2x 4 , 6x 2 , x
Coefficients : 2, 6, 1
Niveau 4
Variable : x
Terme principal : 2x 4
Terme indépendant : n’a pas
Coefficient directeur : 2
Exercice 2
Trouver toutes les parties du polynôme suivant :
![]()
Le polynôme de ce problème est composé de deux variables : x et y. Pourtant:
Termes : -7x 4 y 2 , 3x 4 , -5y 2 , xy, -10
Coefficients : -7, 3, -5, 1, -10
6ème année
Variables : x, y
Terme principal : -7x 4 et 2
Mandat indépendant : -10
Coefficient directeur : -7
Comme vous pouvez le voir, pour résoudre des polynômes comme celui-ci, vous devez savoir comment calculer le degré d’un polynôme avec plus d’une variable. Si vous ne savez toujours pas comment procéder, je vous recommande de consulter le lien ci-dessus dans la section Quelles sont les parties d’un polynôme ? ( degré d’un polynôme de deux variables ). ⬆⬆ Vous y trouverez l’explication étape par étape ainsi que plusieurs exemples.
Bien qu’il s’agisse d’un concept radicalement différent, si vous êtes arrivé jusqu’ici, vous serez sûrement également intéressé à savoir ce qu’est l’ expression polynomiale d’un nombre. C’est quelque chose que peu de gens connaissent mais qui est en fait très utile.