Monômes - Mathority

Nous expliquons ici tout ce que vous devez savoir sur les monômes : ce qu’ils sont, quelles sont leurs parties (et comment les identifier), les différents types de monômes, comment calculer des opérations avec des monômes, la valeur numérique d’un monôme,. .. De plus, vous pourrez voir des exemples et des exercices résolus pas à pas de monômes.

Que sont les monômes ?

En mathématiques, la définition d’un monôme est la suivante :

Un monôme est une expression algébrique formée par une combinaison de chiffres et de lettres. Plus précisément, un monôme est composé du produit entre un nombre et une ou plusieurs variables (lettres) élevées aux exposants.

Par exemple, le terme 7x ³ y ² est appelé un monôme car il a un chiffre (7) et différentes lettres (x, y).

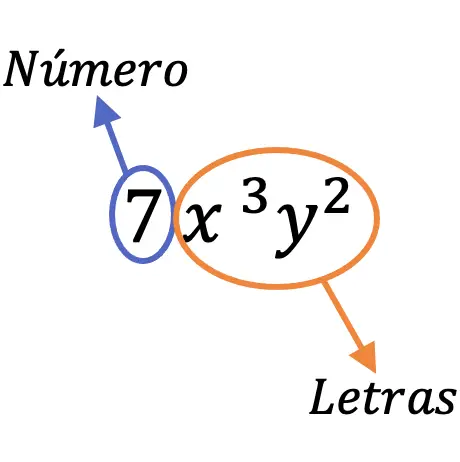
Parties d’un monôme

Maintenant que nous avons vu la signification d’un monôme, voyons ce que sont toutes les parties d’un monôme :

Coefficient : est le nombre qui multiplie les variables (ou lettres) du monôme.
Variable : est chacune des lettres qui apparaissent dans le monôme.
Partie littérale : correspond à toutes les variables qui composent le monôme avec tous leurs exposants respectifs.
Degré : consiste en la somme de tous les exposants des lettres qui forment le monôme.

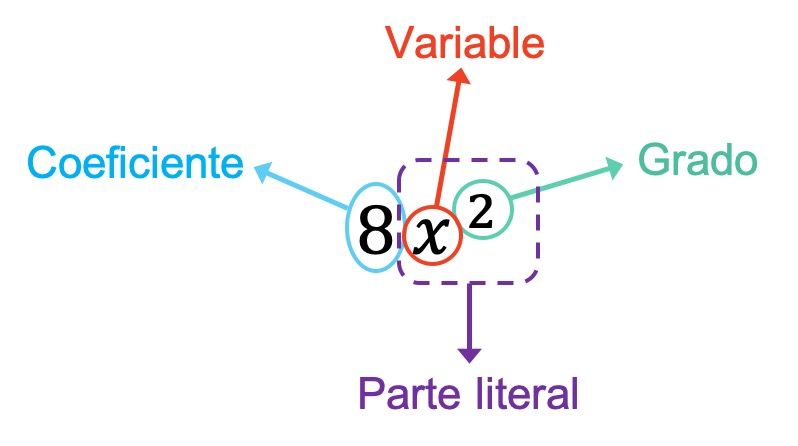
Le coefficient du monôme dans l’exemple ci-dessus est 8 puisque c’est le nombre qui multiplie les variables. De plus, dans ce cas, le monôme n’a qu’une seule variable, qui est x. Ainsi, la partie littérale du monôme est formée par cette variable plus son exposant, c’est x ² . Enfin, le degré du monôme est 2 car c’est le seul exposant qu’il possède.

Essayez maintenant de résoudre l’exercice suivant sur les parties d’un monôme :

Identifiez toutes les parties du monôme suivant :

$5x^4y^2z$

voir solution

Les composants du monôme de l’énoncé sont :

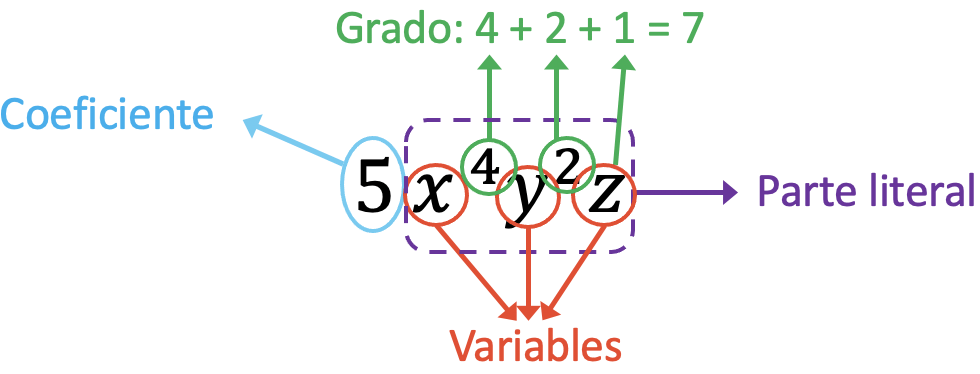
Le coefficient du monôme du problème est 5, puisque c’est le terme qui multiplie les lettres. D’autre part, les variables de ce monôme sont x, y, z. Troisièmement, la partie littérale du monôme correspond à l’expression x ⁴ y ² z. Et enfin, le degré du monôme est égal à la somme de tous les exposants des variables, soit 7 (4+2+1=7).

Notez que lorsqu’une lettre n’a pas d’exposant, cela signifie en fait qu’elle a un 1 comme exposant. Par conséquent, pour calculer le degré du monôme du problème, nous avons ajouté une unité qui représente l’exposant de la variable z.

Types de monômes

Il existe différents types de monômes, chacun ayant ses propres propriétés. Les monômes les plus importants sont les monômes similaires, les monômes homogènes, les monômes hétérogènes et les monômes opposés. Ensuite, nous verrons les caractéristiques de chaque type.

monômes similaires

Les monômes similaires sont les monômes qui ont la même partie littérale. Par conséquent, deux ou plusieurs monômes sont similaires lorsqu’ils ont les mêmes lettres et les mêmes exposants.

Par exemple, les deux monômes suivants sont similaires car, bien qu’ils aient des coefficients différents, ils sont formés par les mêmes variables et élevés aux mêmes exposants.

$4x^5y^3 \qquad \qquad 9x^5y^3$

Comme nous le verrons plus loin, ce type de monômes est utilisé pour résoudre des opérations sur les monômes.

monômes homogènes

Deux monômes sont homogènes lorsque leur degré absolu est égal.

Par exemple, les deux monômes suivants sont homogènes car le degré des deux est égal à 5 :

$2x^5 \qquad \qquad 6x^2y^3$

Le premier monôme a une seule variable qui est élevée à la puissance 5, donc son degré est 5. Et le deuxième polynôme a une variable élevée au carré et une autre élevée au cube, de sorte que son degré est également 5 (2+ 3 =5).

Comme vous pouvez le voir, pour que deux monômes soient homogènes, ils n’ont pas besoin d’avoir la même partie littérale, mais seulement d’avoir le même degré absolu.

monômes hétérogènes

Les monômes hétérogènes sont des monômes qui n’ont pas le même degré absolu. Autrement dit, les monômes hétérogènes sont à l’opposé des monômes homogènes.

Les 3 monômes suivants sont hétérogènes car chacun a un degré différent :

$x^8 \qquad 3xy \qquad 7a^9b^2$

Le premier monôme est de degré 8, le deuxième monôme est de degré 2 et le troisième monôme est de degré 11. Par conséquent, les trois monômes sont hétérogènes les uns aux autres.

Monômes opposés

Les monômes opposés sont les monômes qui sont homogènes (ont la même partie littérale) et, de plus, leurs coefficients sont opposés, c’est-à-dire que leurs coefficients ont la même valeur mais un signe opposé.

Par exemple, les deux monômes suivants sont opposés :

$3x^5y^2 \qquad \qquad -3x^5y^2$

Les deux monômes précédents sont opposés car ils ne diffèrent que par leur signe, le premier a un signe positif et le second un signe négatif.

Maintenant que vous avez vu plusieurs exemples de monômes, vous pourriez être intéressé par une autre expression algébrique similaire : le binôme . En fait, un binôme est constitué de l’addition (ou de la soustraction) de plusieurs monômes, il est donc intéressant de voir la relation entre ces deux concepts. Vous pouvez voir ce que le sens de binôme est en cliquant sur ce lien.

Opérations avec des monômes

Pour approfondir le concept de monôme, nous allons voir quelles opérations peuvent être faites avec les monômes. En particulier, les monômes peuvent être additionnés, soustraits, multipliés, divisés et puissance. Et chaque type d’opération a ses particularités, nous les analyserons donc une par une séparément ci-dessous.

somme de monômes

Deux monômes ou plus ne peuvent être ajoutés que s’il s’agit de monômes similaires. Alors, la somme de deux monômes similaires est égale à un autre monôme composé de la même partie littérale et de la somme des coefficients de ces deux monômes.

Exemples de sommes de monômes

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

Si vous voulez vous entraîner à faire des exercices d’addition de monômes, vous pouvez les rechercher dans le moteur de recherche en haut à droite, car nous avons une page entière pleine d’exercices d’addition de monômes résolus.

soustraction de monômes

Deux monômes ou plus ne peuvent être soustraits que s’ils sont des monômes similaires. Ainsi, la soustraction de deux monômes similaires est égale à un autre monôme composé de la même partie littérale et de la soustraction des coefficients de ces deux monômes.

Exemples de soustraction de monômes

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

Vous pouvez vous entraîner avec les exercices résolus étape par étape de soustraction de monômes qui se trouvent sur notre site Web. Vous pouvez les trouver via le moteur de recherche en haut à droite.

multiplication de monômes

Le résultat de la multiplication de deux monômes est un autre monôme dont le coefficient est le produit des coefficients des monômes et dont la partie littérale s’obtient en multipliant les variables qui ont la même base, c’est-à-dire en additionnant leurs exposants.

Ainsi, pour résoudre le produit entre deux monômes différents, les coefficients doivent être multipliés ensemble et les exposants des puissances qui ont la même base doivent être ajoutés.

D’autre part, si nous multiplions deux monômes avec une puissance de base différente, nous devons simplement multiplier leurs coefficients ensemble et laisser les puissances identiques :

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Exemples de multiplication de monômes

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Pour pratiquer avec des exercices résolus étape par étape de multiplication de monômes, vous pouvez consulter l’article que nous avons sur ce site. Vous le trouverez facilement avec le moteur de recherche en haut à droite.

division de monômes

Le résultat de la division des monômes est un autre monôme dont le coefficient est équivalent au quotient des coefficients des monômes et dont la partie littérale s’obtient en divisant les variables qui ont la même base, c’est-à-dire en soustrayant leurs exposants.

Donc, pour diviser deux monômes différents, nous divisons simplement les coefficients entre eux et soustrayons les exposants des puissances qui ont la même base.

Exemples de divisions de monômes

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

La division des monômes est plus difficile qu’il n’y paraît, nous vous recommandons donc d’essayer de faire les exercices résolus étape par étape que nous avons sur la division des monômes . Le moyen le plus rapide de les trouver est via notre moteur de recherche en haut à droite.

puissance d’un monôme

Pour calculer la puissance d’un monôme, chaque élément du monôme doit être élevé à l’exposant de puissance . Autrement dit, la puissance d’un monôme consiste à élever son coefficient et ses variables (lettres) à l’exposant de la puissance.

Rappelez-vous des propriétés des puissances que lorsque nous élevons un terme qui est déjà élevé, les deux exposants sont multipliés ensemble. Pour cette raison , dans la puissance d’un monôme, l’exposant de chaque lettre est toujours multiplié par l’exposant qui indique la puissance .

Exemples de puissances de monômes

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Il est assez facile de se tromper dans ce type d’opération avec des monômes. C’est pourquoi nous vous recommandons de vous entraîner avec les exercices que nous avons résolus étape par étape sur notre site Web. Vous les trouverez rapidement en les recherchant dans le moteur de recherche en haut à droite.

Valeur numérique d’un monôme

La valeur numérique d’un monôme est le résultat obtenu en substituant les variables d’un monôme à certaines valeurs.

Par exemple, si nous avons le monôme suivant :

$5x^2$

Si nous voulons trouver la valeur numérique du monôme précédent pour

$x=2$ il faut remplacer la lettre $x$ du monôme par 2 et résoudre les opérations résultantes :

$5\cdot 2^2= 5 \cdot 4 = 20$

Donc la valeur numérique du monôme

$5x^2$ pour $x=2$ est égal à 20.

Vous pouvez également déterminer la valeur numérique d’un monôme multivariable. Par exemple, si nous avons le monôme bivariable suivant, ou en d’autres termes, à deux variables :

$3x^4y$

Pour calculer la valeur numérique du monôme ci-dessus lorsque

$x$ vaut 1 e $y$ vaut -2, on substitue les lettres à leurs valeurs respectives :

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

Donc la valeur numérique du monôme du problème pour

$x=1$ et $y=-2$ renvoie -6.

Monômes et polynômes

Enfin, sachez que les polynômes peuvent être formés à partir de monômes :

Un polynôme est le groupement de deux monômes ou plus.

$P(x)= 4x^5+3x^2-7x$

Par exemple, le polynôme précédent résulte de l’addition (ou de la soustraction) de 3 monômes hétérogènes.

Par curiosité, lorsqu’un polynôme n’a que 2 monômes, on l’appelle un binôme . Et lorsqu’un polynôme a exactement 3 monômes, on l’appelle un trinôme .

Si vous voulez en savoir plus sur les polynômes, vous pouvez consulter la page principale du Web, où nous expliquons tout ce que vous devez savoir sur les polynômes.