Opérations avec des monômes -

Sur cette page nous expliquons comment effectuer toutes les opérations avec les monômes (addition, soustraction, multiplication, division et puissance). De plus, vous pourrez voir des exemples de chaque type d’opération avec des monômes et vous entraîner avec des exercices résolus étape par étape.

Addition et soustraction de monômes

Deux monômes ou plus ne peuvent être ajoutés ou soustraits que s’ils sont des monômes similaires, c’est-à-dire si les deux monômes ont une partie littérale identique (mêmes lettres et mêmes exposants).

Alors, la somme (ou soustraction) de deux monômes similaires est égale à un autre monôme composé de la même partie littérale et de la somme (ou soustraction) des coefficients de ces deux monômes.

que sont les opérations avec les monômes

L’addition et la soustraction de monômes sont également appelées respectivement addition et soustraction de monômes.

Exemples d’addition et de soustraction de monômes

Pour que vous puissiez bien comprendre comment ajouter et soustraire deux monômes ou plus, nous vous laissons ci-dessous plusieurs exemples :

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

Les monômes du dernier exemple ne peuvent pas être ajoutés ou soustraits car ils ne sont pas similaires ou, en d’autres termes, ils ont des inconnues ou des exposants différents.

Produit d’un nombre de fois un monôme

Pour résoudre le produit d’un monôme par un nombre, il suffit de multiplier le coefficient du monôme par ce nombre, en laissant la partie littérale du monôme identique.

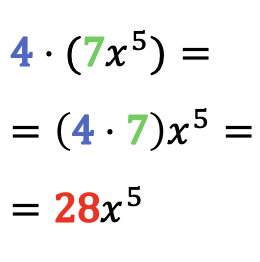
Exemples de multiplication de nombres par des monômes

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

Multiplication des monômes

Le résultat de la multiplication de deux monômes est un autre monôme dont le coefficient est le produit des coefficients des monômes et dont la partie littérale est obtenue en multipliant les variables qui ont la même base, c’est-à-dire en additionnant leurs exposants.

Par conséquent, pour multiplier deux monômes différents, il faut multiplier les coefficients entre eux et additionner les exposants des puissances qui ont la même base.

Cependant, si nous multiplions deux monômes avec une puissance de base différente , nous devons simplement multiplier leurs coefficients ensemble et laisser les puissances identiques. Par exemple:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

En revanche, lors de la multiplication de monômes, il faut tenir compte de la règle des signes :

Un monôme positif multiplié par un monôme positif donne un autre monôme positif.
Un monôme positif multiplié par un monôme négatif (ou vice versa) équivaut à un monôme négatif.
Deux monômes négatifs multipliés ensemble donnent naissance à un monôme positif.

Exemples de multiplications de monômes

Vous trouverez ci-dessous plusieurs exemples de multiplication entre monômes afin que vous puissiez voir comment cela se fait :

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Comme vous l’avez vu, résoudre une multiplication de monômes est relativement simple. Mais vous devez garder à l’esprit que les monômes peuvent également être multipliés par des polynômes, et même 2 polynômes ou plus peuvent être multipliés ensemble. Si vous êtes plus intéressé, vous pouvez voir comment se déroulent toutes ces opérations en cliquant sur multiplication polynomiale .

Division des monômes

En mathématiques, le résultat de la division des monômes est un autre monôme dont le coefficient est équivalent au quotient des coefficients des monômes et dont la partie littérale est obtenue en divisant les variables qui ont la même base, c’est-à-dire en soustrayant leurs exposants.

Évidemment, toute division de monômes peut également être exprimée sous forme de fraction :

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

Comme dans la multiplication, dans la division des monômes il faut appliquer la loi des signes :

Un monôme positif divisé par un monôme positif donne un autre monôme positif.
Un monôme positif divisé par un monôme négatif (ou vice versa) équivaut à un monôme négatif.
Deux monômes négatifs divisés l’un par l’autre donnent naissance à un monôme positif.

Exemples de divisions de monômes

Vous pouvez voir plus d’exemples de la façon dont deux ou plusieurs monômes sont divisés ci-dessous :

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Sûrement à un moment donné, lorsque vous avez appris quelque chose de nouveau en mathématiques, vous vous êtes demandé : à quoi ça sert ? Eh bien, la division des monômes est utilisée pour diviser des polynômes. En fait, il est assez courant de faire une erreur en divisant des polynômes parce que deux monômes ont été mal divisés. C’est pourquoi nous vous recommandons, maintenant que vous êtes familier avec la division entre monômes, de voir comment est calculée la division des polynômes , car il vous sera maintenant beaucoup plus facile d’apprendre la procédure (c’est assez compliqué).

Pouvoir d’un monôme

En mathématiques, pour calculer la puissance d’un monôme, chaque élément du monôme est élevé à l’exposant de la puissance . Autrement dit, la puissance d’un monôme consiste à élever son coefficient et ses variables (lettres) à l’exposant de la puissance.

comment les opérations avec les monômes sont résolues

Rappelez-vous des propriétés des puissances que lorsque l’on élève un terme déjà élevé, les deux exposants se multiplient. C’est pourquoi , à la puissance d’un monôme, l’exposant de chaque lettre est toujours multiplié par l’exposant qui indique la puissance .

Par contre, pour effectuer correctement cette opération vous devez retenir la propriété suivante des puissances :

Un monôme négatif élevé à un exposant pair équivaut à un monôme positif.
Au lieu de cela, un monôme négatif élevé à un exposant impair donne un monôme négatif.

Exemples de pouvoirs des monômes

Nous vous laissons quelques exemples pour que vous puissiez bien comprendre comment se calcule la puissance d’un monôme :

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

Opérations combinées avec des monômes

Une fois que vous avez vu ce que sont toutes les opérations avec les monômes, sachez qu’elles peuvent également être combinées entre elles. C’est-à-dire que nous pouvons trouver des exercices dans lesquels on nous demande de résoudre des opérations avec des monômes où tous les types sont impliqués : addition, soustraction, multiplication, division et puissances.

Mais ne vous inquiétez pas, ils ne sont pas aussi difficiles qu’il y paraît. La seule chose dont vous devez vous souvenir est l’ordre dans lequel les opérations combinées sont résolues :

Tout d’abord, les opérations avec les monômes entre parenthèses sont résolues.
Ensuite, les puissances des monômes sont calculées.
Troisièmement, les multiplications et divisions des monômes sont effectuées.
Et enfin, les additions et soustractions de monômes sont déterminées.

Je suis sûr qu’en résolvant un exemple, vous le verrez plus clairement :

Exemple d’opération combinée de monômes

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

Tout d’abord, il faut résoudre les opérations avec des monômes entre parenthèses :

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

Dans ce cas, nous n’avons aucun pouvoir. Alors maintenant, calculons les multiplications et divisions des monômes :

$-2x^5+18x^5 - 7x^5$

Et enfin, on fait l’addition et la soustraction de monômes :

$16x^5 - 7x^5$

$\bm{9x^5}$

Exercices résolus sur les opérations avec des monômes

Au cas où vous souhaiteriez vous entraîner, nous vous laissons ci-dessous plusieurs exercices résolus étape par étape de difficulté ESO sur les opérations avec des monômes.

Exercice 1

Calculez les additions et soustractions suivantes de monômes :

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

Voir la solution

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

Exercice 2

Résolvez les multiplications de monômes suivantes :

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

Voir la solution

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}$

Exercice 3

Déterminez le résultat des divisions de monômes suivantes :

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

Voir la solution

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

Dans l’opération précédente nous avons simplifié le terme

$y^0$ car tout nombre élevé à 0 est égal à 1. Donc :

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}$

Exercice 4

Trouvez les puissances suivantes des monômes :

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

Voir la solution

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

Exercice 5

Résolvez les opérations suivantes combinées avec des monômes et simplifiez autant que possible :

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

Voir la solution

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

L’opération ne peut pas être simplifiée davantage car les deux monômes ont des exposants différents, le résultat est donc un polynôme.

Si vous êtes arrivé jusqu’ici, cela signifie que vous maîtrisez déjà toutes les opérations avec les monômes. Brillant! Eh bien, une autre opération qui va sûrement vous intéresser est la factorielle d’un nombre. Il s’agit d’une opération assez curieuse, puisqu’elle se calcule différemment des autres. Et, en fait, beaucoup de gens ne savent pas ce qu’est la factorielle d’un nombre. Découvrez comment résoudre une factorielle en cliquant sur ce lien.

Addition et soustraction de monômes

Exemples d’addition et de soustraction de monômes

Produit d’un nombre de fois un monôme

Exemples de multiplication de nombres par des monômes

Multiplication des monômes

Exemples de multiplications de monômes

Division des monômes

Exemples de divisions de monômes

Pouvoir d’un monôme

Exemples de pouvoirs des monômes

Opérations combinées avec des monômes

Exemple d’opération combinée de monômes

Exercices résolus sur les opérations avec des monômes

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply