▷ Comment multiplier des polynômes (exercices résolus)

Sur cette page, vous découvrirez comment les polynômes sont multipliés. Vous pourrez également voir des exemples de multiplications de polynômes et, en plus, des exercices résolus étape par étape. Enfin, vous découvrirez quelles sont les propriétés des polynômes multiplicateurs.

Cependant, pour bien comprendre le concept de multiplication de polynômes, nous passerons du plus basique au plus compliqué, c’est-à-dire que nous commencerons par comment multiplier un polynôme par un nombre, puis nous verrons comment multiplier un polynôme par un monôme et, enfin, nous expliquerons comment multiplier deux ou plusieurs polynômes entre eux.

Je vous conseille de suivre cet ordre, mais si vous pensez maîtriser déjà les opérations avec les polynômes précédents vous pouvez passer directement à la multiplication entre polynômes en cliquant sur l’index :

Multiplier un polynôme par un nombre

Le produit d’un scalaire (ou d’un nombre) et d’un polynôme est assez simple à résoudre, il suffit de multiplier le nombre par le coefficient de chaque terme du polynôme .

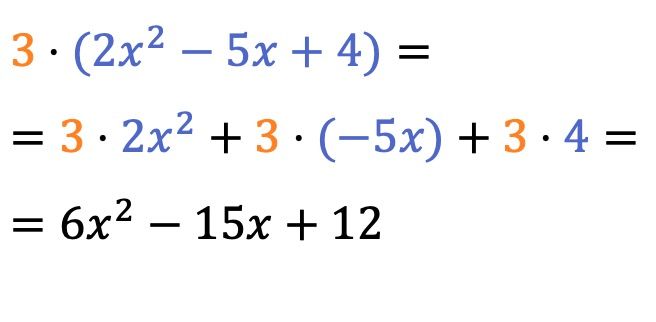
multiplication d'un nombre par un polynôme

Le signe de multiplication devant les parenthèses peut être omis.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

Multiplication d’un polynôme par un monôme

Avant de voir comment multiplier un polynôme par un monôme, nous allons d’abord rappeler comment les monômes se multiplient entre eux, car il faut le connaître pour pouvoir faire ce type d’opération polynomiale.

Le produit de deux monômes consiste à multiplier leurs coefficients entre eux et leurs parties littérales entre elles, c’est-à-dire que les coefficients des monômes sont multipliés et que les exposants des variables qui ont la même base sont ajoutés. Regardez l’exemple suivant :

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

Voyons maintenant comment multiplier un monôme par un polynôme :

En mathématiques, pour résoudre la multiplication d’un monôme par un polynôme, le monôme est multiplié par chaque terme du polynôme.

multiplication d'un polynôme par un monôme

Comme précédemment, le signe de multiplication peut également être omis :

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Remarquez dans l’exemple précédent que lorsqu’on multiplie des monômes ou des polynômes il faut aussi prendre en compte la règle des signes. En fait, une erreur très courante lors de la multiplication de monômes et de polynômes est de se tromper sur le signe d’un terme.

Sûrement à un moment donné, lorsque vous avez vu quelque chose de nouveau en mathématiques, vous vous êtes demandé : à quoi ça sert ? Eh bien, ce type de multiplication sert à obtenir le facteur commun d’un polynôme , une opération qui permet de simplifier les polynômes (très utile). Vous pouvez voir de quoi il s’agit et comment le facteur commun d’un polynôme est calculé dans ce lien.

Multiplication de deux polynômes

Une fois que nous savons comment multiplier des polynômes par des nombres et par des monômes, voyons ce que c’est et comment multiplier des polynômes par des polynômes.

Pour multiplier des polynômes, suivez les étapes suivantes :

Multipliez chaque terme du premier polynôme par tous les termes du deuxième polynôme.
Ajoutez (ou soustrayez) des monômes du même degré (monômes similaires).

Pour que vous puissiez voir exactement en quoi consiste cette méthode, nous allons résoudre étape par étape la multiplication de polynômes suivante :

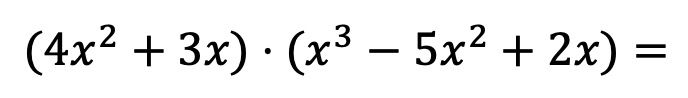
Tout d’abord, il faut multiplier chaque élément du premier polynôme multiplicateur par chaque terme du deuxième polynôme :

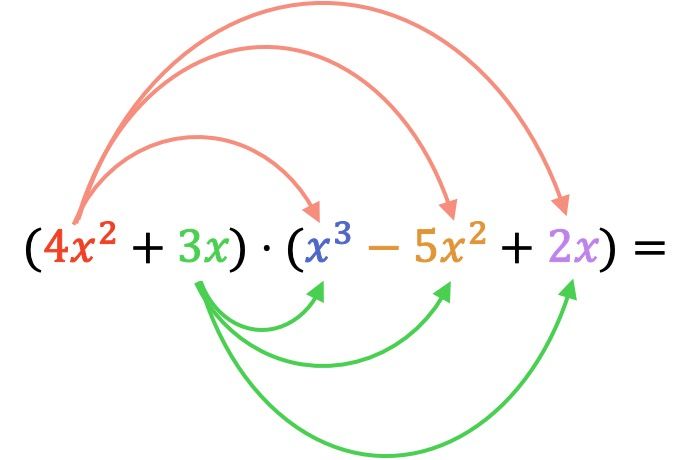
multiplication de polynômes étape par étape

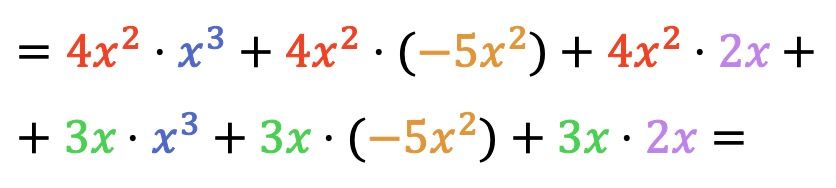
Maintenant, nous faisons toutes les multiplications de monômes :

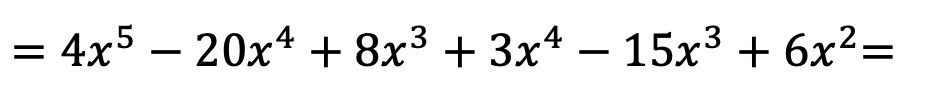
Une fois que nous avons multiplié les polynômes entre eux, il suffit de regrouper les termes résultants qui sont similaires, c’est-à-dire les termes ayant la même lettre et le même exposant :

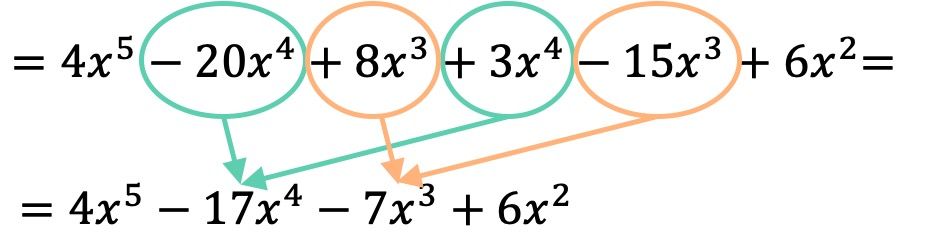
multiplication de polynômes par polynômes

Le résultat de la multiplication polynomiale est donc :

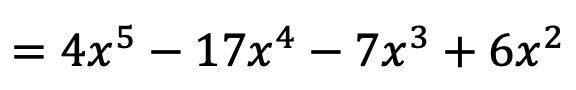
Et de cette façon nous avons déjà calculé la multiplication des polynômes. Peut-être que cela vous semble très difficile maintenant, mais vous verrez que lorsque vous pratiquez avec deux ou trois exercices, ce sera beaucoup plus facile.

Maintenant que vous avez vu comment est résolue la multiplication entre deux polynômes, vous êtes probablement intéressé de savoir comment diviser des polynômes . En fait, diviser des polynômes est bien plus compliqué que les multiplier, c’est pourquoi nous vous avons expliqué la procédure (et les astuces) étape par étape pour que vous puissiez parfaitement la comprendre. Si vous êtes intéressé, cliquez sur ce lien pour voir comment les polynômes sont divisés.

Multiplication polynomiale verticale

Nous venons de voir comment multiplier un polynôme par un autre polynôme horizontalement, mais cela peut aussi se faire de manière plus classique : multiplier des polynômes verticalement. Voyons comment cette méthode est utilisée en résolvant un exemple de multiplication polynomiale.

Si l’on veut multiplier verticalement les deux polynômes suivants :

$(5x^2+3x-4) \cdot (2x^2-x)$

La première chose que nous devons faire est de placer un polynôme en dessous de l’autre, sous forme de multiplication algébrique de polynômes :

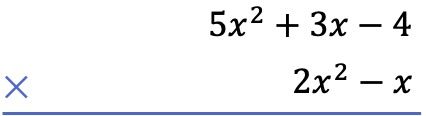
Deuxièmement, on multiplie chaque terme du polynôme ci-dessous par chaque terme du polynôme ci-dessus, et on met les résultats classés par colonnes du degré le plus élevé au degré le plus bas :

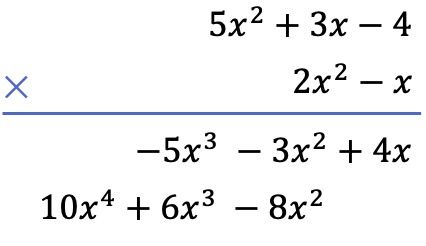
Et enfin, nous ajoutons les termes alignés verticalement :

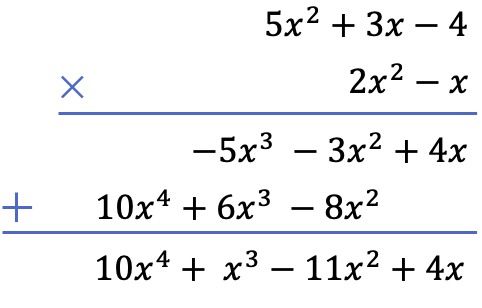
Maintenant que vous avez vu les 2 méthodes qui existent pour résoudre une multiplication de polynômes, saviez-vous qu’on peut aussi multiplier des fractions avec des polynômes ? Et pas seulement des multiplications, mais toutes sortes d’opérations peuvent être effectuées avec ces types de fractions. Cliquez sur ce lien et découvrez ce que sont les fractions algébriques .

Propriétés de la multiplication polynomiale

La multiplication de polynômes répond aux caractéristiques suivantes :

Propriété commutative : l’ordre des polynômes multiplicateurs ne modifie pas le résultat de la multiplication.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

Propriété associative : lorsque trois polynômes ou plus sont multipliés, le résultat du produit est le même quelle que soit la façon dont les facteurs sont regroupés :

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Propriété distributive : la somme de deux polynômes multipliée par un tiers est égale à la somme de chaque addition multipliée par le troisième polynôme.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

Le degré du polynôme résultant d’une multiplication entre deux polynômes est égal à la somme des degrés des deux polynômes multipliés.

Exercices résolus sur la multiplication de polynômes

Pour que vous puissiez vous entraîner, je vous laisse avec plusieurs exercices résolus sur la multiplication des polynômes. Vous pouvez essayer de les résoudre vous-même et vérifier vos résultats avec la solution proposée. Vous pouvez alors nous poser toutes vos questions dans les commentaires, nous serons ravis de vous aider.

Exercice 1

Calculez les produits suivants entre polynômes et scalaires :

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

Voir la solution

Pour calculer la multiplication d’un polynôme par un nombre il faut multiplier le nombre par le coefficient de chaque élément du polynôme. Donc:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Exercice 2

Résolvez les multiplications suivantes entre polynômes et monômes :

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

Voir la solution

Pour résoudre la multiplication d’un polynôme par un monôme il faut multiplier ledit monôme par chaque terme du polynôme. Donc:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Exercice 3

Déterminez le résultat des multiplications suivantes entre polynômes :

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

Voir la solution

Pour calculer une multiplication de deux polynômes, nous devons multiplier chaque élément du premier polynôme par chaque élément du deuxième polynôme, puis regrouper les termes similaires. Donc:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Exercice 4

Trouvez le résultat des multiplications suivantes entre polynômes :

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

Voir la solution

Pour calculer une multiplication de deux polynômes, nous devons multiplier chaque élément du premier polynôme par chaque élément du deuxième polynôme, puis ajouter les termes similaires. Donc:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Exercice 5

Calculez les multiplications de polynômes suivantes :

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

Voir la solution

Pour faire un produit de 2 polynômes, il faut multiplier chaque terme du premier polynôme par chaque terme du deuxième polynôme, puis regrouper les monômes similaires obtenus. Pourtant:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Exercice 6

Résolvez la multiplication suivante de 3 polynômes :

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

Voir la solution

Le fonctionnement du problème consiste en 2 multiplications de polynômes, plus précisément il est composé de deux binômes et d’un trinôme. Nous devons donc d’abord résoudre un produit, puis multiplier le résultat par le polynôme restant.

On calcule donc la première multiplication :

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

Et maintenant, nous résolvons la multiplication restante :

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Exercice 7

Multipliez les polynômes suivants avec des coefficients rationnels (avec des fractions) :

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

Voir la solution

Bien que les polynômes aient des fractions, il s’agit toujours d’une multiplication entre deux polynômes. Il faut donc le résoudre comme n’importe quel produit polynomial : multiplier tous les éléments entre eux puis regrouper les monômes similaires.

On multiplie donc les polynômes :

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

Et, pour finir, on ajoute (ou soustrait) les termes dont les parties littérales sont identiques :

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

Pour bien réaliser cet exercice, il était important que vous maîtrisiez les opérations avec les fractions. Mais si vous avez des questions sur une étape, vous pouvez les poser dans les commentaires et nous y répondrons le plus rapidement possible.

Multiplication (ou produit) de polynômes

Multiplier un polynôme par un nombre

Multiplication d’un polynôme par un monôme

Multiplication de deux polynômes

Multiplication polynomiale verticale

Propriétés de la multiplication polynomiale

Exercices résolus sur la multiplication de polynômes

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Leave a Comment Cancel Reply