Fractions algébriques : simplification, opérations, exercices résolus,… -

Sur cette page, nous expliquons ce que sont les fractions algébriques, quand elles sont équivalentes, comment les simplifier et comment effectuer des opérations avec des fractions algébriques (addition, soustraction, multiplication et division). De plus, vous pourrez voir des exercices résolus étape par étape pour les fractions algébriques. Bref, vous trouverez ici tout sur les fractions algébriques.

Que sont les fractions algébriques ?

En mathématiques, une fraction algébrique est une fraction qui a un polynôme au numérateur et un autre polynôme au dénominateur.

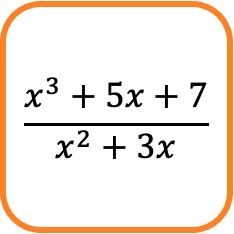
Par exemple, l’expression fractionnaire ci-dessus consiste en une fraction algébrique car son numérateur et son dénominateur sont constitués de polynômes.

Fractions algébriques équivalentes

Une fois que nous connaissons la définition des fractions algébriques, voyons quand deux fractions de ce type sont égales.

Mathématiquement, deux fractions algébriques sont équivalentes si la condition suivante est remplie :

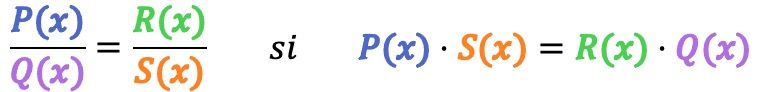
$exemples de fractions algébriques équivalentes$

A titre d’exemple, nous allons vérifier si les 2 fractions algébriques suivantes sont équivalentes :

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Pour déterminer si les fractions sont algébriquement égales, on multiplie leurs termes transversalement :

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Calculons maintenant les multiplications de polynômes :

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Nous avons obtenu la même expression des deux côtés de l’équation, ce sont donc effectivement deux fractions algébriques équivalentes.

Simplifier les fractions algébriques

Pour simplifier une fraction algébrique, il faut d’abord factoriser les polynômes du numérateur et du dénominateur, puis éliminer les facteurs qu’ils ont en commun.

Évidemment, afin de simplifier les fractions algébriques, il est essentiel que vous sachiez ce qu’est la factorisation des polynômes et comment cela se fait. Si vous ne savez toujours pas comment les polynômes sont factorisés ou si vous ne vous en souvenez pas complètement, je vous recommande d’aller sur la page liée avant de continuer, sinon vous comprendrez à peine la procédure. On y explique étape par étape comment factoriser des polynômes et, en plus, vous pourrez voir plusieurs exemples et vous entraîner avec des exercices résolus.

Voyons maintenant comment une fraction algébrique est simplifiée en appliquant la méthode de factorisation des polynômes à l’aide d’un exemple :

Simplifiez la fraction algébrique suivante :

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Tout d’abord, on factorise les polynômes du numérateur et du dénominateur de la fraction :

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Si vous ne savez pas comment les polynômes ont été factorisés, jetez un œil au lien ci-dessus)⬆

Et une fois que nous avons factorisé les polynômes, nous éliminons les facteurs communs entre le numérateur et le dénominateur, c’est-à-dire que nous supprimons tous les termes qui sont répétés :

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

La fraction algébrique simplifiée ressemble donc à ceci :

$\cfrac{(x+1)(x+2)}{x-1}$

Dans ce problème, les polynômes de la fraction algébrique ont été factorisés en trouvant leurs racines ; cependant, parfois un polynôme peut être factorisé directement en prenant le facteur commun (méthode beaucoup plus rapide). Dans ce lien, vous verrez ce que signifie prendre un facteur commun à partir d’un polynôme et vous découvrirez comment simplifier une fraction algébrique en utilisant un facteur commun.

Opérations avec des fractions algébriques

Comme tout type de fractions, des opérations peuvent également être effectuées avec des fractions algébriques. Plus précisément, les fractions algébriques peuvent être additionnées, soustraites, multipliées et divisées. Ci-dessous, nous expliquons étape par étape avec des exemples comment chaque type d’opération est calculé.

Addition et soustraction de fractions algébriques

La procédure d’addition et de soustraction de fractions algébriques est pratiquement identique, nous les analyserons donc ensemble. Nous verrons d’abord un exemple de deux fractions algébriques ajoutées et, ci-dessous, nous étudierons la différence entre la méthode de soustraction de fractions algébriques.

Addition de fractions algébriques

L’addition de fractions algébriques se fait de la même manière qu’avec les fractions normales : réduisez d’abord les fractions à un dénominateur commun puis additionnez les numérateurs.

Voyons comment les fractions algébriques sont ajoutées à l’aide d’un exemple :

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Nous factorisons d’abord les dénominateurs des fractions :

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Il faut maintenant trouver le lcm (plus petit commun multiple) des dénominateurs pour réduire les fractions à un dénominateur commun.

Astuce : le lcm des dénominateurs est toujours formé du produit des facteurs qu’ils ont en commun élevé au plus grand exposant multiplié par les facteurs non communs .

Par exemple, dans notre cas

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Le diviseur commun entre les dénominateurs élevés au plus grand exposant est $(x+1)^2.$

Et le facteur non commun entre les dénominateurs est $x.$

Par conséquent, le lcm des dénominateurs dans ce cas est : $(x+1)^2 \cdot x$

Le lcm des dénominateurs est donc

$(x+1)^2 \cdot x,$ ce sera donc le nouveau dénominateur des 2 fractions.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Une fois qu’on a trouvé le dénominateur commun, il faut modifier les numérateurs. Pour ce faire, on suit le même processus que pour l’addition de fractions normales : pour chaque fraction on divise le lcm

$\bigl( \ x(x+1)^2 \ \bigr)$ entre le dénominateur d’origine et multipliez le résultat par le numérateur :

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Alors maintenant, nous pouvons rassembler les deux fractions car elles ont le même dénominateur :

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Enfin, nous opérons sur le numérateur. On fait d’abord le produit du monôme et du polynôme :

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Ensuite, nous ajoutons les termes similaires au numérateur :

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Normalement, nous en serions déjà là, mais si nous examinons ce problème de près, nous pouvons encore simplifier davantage la fraction algébrique en supprimant un facteur commun au numérateur. Pourtant:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

Et ainsi nous avons déjà terminé la somme des deux fractions algébriques.

Soustraction de fractions algébriques

Pour soustraire des fractions algébriques, nous devons appliquer une procédure similaire à celle de l’addition de fractions algébriques : d’abord réduire les fractions à un dénominateur commun, puis soustraire les numérateurs.

Voyons comment les fractions algébriques sont soustraites avec un exemple :

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Tout d’abord, nous devons factoriser les dénominateurs des deux fractions :

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Comme pour la soustraction de fractions normales, il faut maintenant calculer le lcm (plus petit commun multiple) des dénominateurs pour réduire les fractions à un dénominateur commun. Dans ce cas, le lcm des dénominateurs est

$(x+2)^2(x-3) ,$ ce sera donc le nouveau dénominateur des 2 fractions.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Maintenant, nous appliquons le même processus que pour la soustraction de fractions normales : pour chaque fraction, nous divisons le lcm

$\bigl( \ x(x+1)^2 \ \bigr)$ entre le dénominateur d’origine et multipliez le résultat par le numérateur :

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

On joint maintenant les deux fractions algébriques puisqu’elles ont le même dénominateur :

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

Et on opère sur le numérateur. Nous résolvons d’abord les multiplications polynomiales :

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Une erreur très courante lors de la soustraction de fractions algébriques est d’oublier de mettre une parenthèse après avoir effectué cette multiplication. Ce serait une erreur puisque le signe négatif affecte tous les éléments résultants du produit, et pas seulement le premier terme.

Nous effectuons les opérations entre parenthèses :

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Ainsi, grâce au signe négatif, on change le signe de tous les termes entre parenthèses :

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

Et, pour finir, nous regroupons les monômes similaires :

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Multiplication de fractions algébriques

Pour multiplier des fractions algébriques, on factorise d’abord tous les polynômes desdites fractions, ensuite on multiplie les numérateurs entre eux et les dénominateurs entre eux et, enfin, on simplifie la fraction obtenue.

Par conséquent, le produit de fractions algébriques est en fait calculé de la même manière que le produit de fractions normales.

Voyons ensuite comment multiplier deux fractions algébriques avec un exemple :

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Tout d’abord il faut factoriser tous les polynômes des fractions, aussi bien les numérateurs que les dénominateurs :

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Maintenant, multiplions les fractions. Pour ce faire, on multiplie les numérateurs et les dénominateurs entre eux :

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

Et enfin, nous simplifions les facteurs qui sont répétés au dénominateur et au numérateur :

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Le résultat de la multiplication est donc :

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

La fraction ne peut pas être simplifiée davantage. Nous avons donc déjà fini de multiplier des fractions algébriques.

Division de fractions algébriques

Pour calculer une division de fractions algébriques , on factorise d’abord tous les polynômes, puis on multiplie les fractions transversalement (le premier numérateur par le deuxième dénominateur et le premier dénominateur par le deuxième numérateur) et enfin, on simplifie la fraction algébrique.

Voyons donc mieux comment deux fractions algébriques sont divisées à l’aide d’un exemple :

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

La première étape pour diviser deux fractions algébriques consiste à factoriser tous les polynômes impliqués dans l’opération :

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Il faut maintenant diviser les fractions. Pour ce faire, on multiplie les fractions transversalement, c’est-à-dire que le premier numérateur est multiplié par le deuxième dénominateur et le résultat sera le numérateur de la nouvelle fraction, et, de la même manière, le premier dénominateur est multiplié par le deuxième numérateur et le résultat sera le dénominateur de la nouvelle fraction :

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Nous simplifions les facteurs qui sont répétés au dénominateur et au numérateur :

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

Et nous pouvons encore simplifier davantage la fraction, puisque

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

La fraction ne peut pas être simplifiée davantage. Par conséquent, nous avons déjà divisé les fractions algébriques.

Exercices résolus sur les fractions algébriques

Ci-dessous nous vous proposons plusieurs exercices résolus étape par étape sur les fractions algébriques, afin que vous puissiez vous entraîner et ainsi finir de comprendre le concept. N’oubliez pas que vous pouvez nous poser toutes vos questions ci-dessous dans les commentaires ! 💬💬💬

Exercice 1

Déterminez si les fractions algébriques suivantes sont équivalentes ou non :

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Voir la solution

Pour vérifier si deux fractions algébriques sont équivalentes, il faut les multiplier transversalement et voir si on obtient une égalité. Nous allons donc d’abord vérifier la première et la deuxième fraction :

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

On résout l’identité notable à gauche de l’équation :

$x^2-9=x^2-9$ ✅

Dans ce cas, nous avons obtenu une égalité, de sorte que les première et deuxième fractions sont algébriquement égales.

Nous appliquons maintenant la même procédure avec la première et la troisième fraction algébrique :

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$ ❌

Cependant, cette fois, les fractions algébriques ne satisfont pas à l’équation, donc les première et troisième fractions sont mathématiquement différentes.

En conclusion, la troisième fraction est différente de la première fraction et, par conséquent, elle est également inégale à la deuxième fraction puisque les première et deuxième fractions sont équivalentes.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Exercice 2

Simplifiez les fractions algébriques suivantes :

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Voir la solution

Pour simplifier une fraction algébrique, nous devons factoriser les polynômes du numérateur et du dénominateur, puis éliminer les facteurs répétés. Pourtant:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Exercice 3

Calculez les additions et soustractions suivantes de fractions algébriques :

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Voir la solution

Pour additionner (ou soustraire) des fractions algébriques, nous devons d’abord réduire les fractions à un dénominateur commun, puis ajouter (ou soustraire) les numérateurs. Donc:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Exercice 4

Résolvez les multiplications et divisions suivantes de fractions algébriques :

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Voir la solution

Pour multiplier des fractions algébriques, nous devons d’abord factoriser tous les polynômes, puis multiplier les numérateurs et les dénominateurs ensemble et enfin simplifier la fraction obtenue.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Par contre, pour diviser des fractions algébriques on factorise d’abord tous les polynômes, puis on multiplie les fractions transversalement (le premier numérateur par le deuxième dénominateur et le premier dénominateur par le deuxième numérateur) et, enfin, on simplifie la fraction algébrique trouvée.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Qu’avez-vous pensé de l’explication ? Avez-vous apprécié? Ou avez-vous des suggestions ? 💬 Dites-nous ce que vous pensez de cette page dans les commentaires ! On vous lit tous ! 👀 Et n’oubliez pas que vous pouvez également nous poser toutes vos questions ! ❔👇❔👇

Que sont les fractions algébriques ?

Fractions algébriques équivalentes

Simplifier les fractions algébriques

Opérations avec des fractions algébriques

Addition et soustraction de fractions algébriques

Addition de fractions algébriques

Soustraction de fractions algébriques

Multiplication de fractions algébriques

Division de fractions algébriques

Exercices résolus sur les fractions algébriques

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply