▷ Comment supprimer (ou extraire) le facteur commun ✅ (exercices résolus)

Sur cette page nous expliquons comment prendre (ou extraire) le facteur commun d’un polynôme. Vous trouverez ici les différents types de facteur commun et vous pourrez voir plusieurs exemples de la façon dont cela est réalisé. De plus, vous pouvez vous entraîner avec des exercices résolus étape par étape.

Quel est le facteur commun ?

En mathématiques, le facteur commun est un facteur présent dans tous les termes d’un polynôme, c’est-à-dire que le facteur commun est constitué d’un nombre ou d’une lettre qui multiplie chaque terme d’un polynôme.

A titre d’exemple, nous allons identifier quel est le facteur commun du polynôme suivant :

$4x+4y$

Au numéro 4 il est répété dans tous les termes du polynôme :

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

Le facteur commun de ce polynôme est donc égal à 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

Comment obtenir (ou extraire) le facteur commun

Une fois que nous connaissons la signification du facteur commun, voyons comment obtenir le facteur commun à partir d’un polynôme.

Lorsque deux ou plusieurs termes d’un polynôme ont un facteur commun, le facteur commun peut être pris (ou extrait) pour transformer les additions ou soustractions du polynôme en une multiplication.

Cela peut vous paraître un peu difficile à écrire, voyons donc comment extraire le facteur commun d’un polynôme avec un exemple :

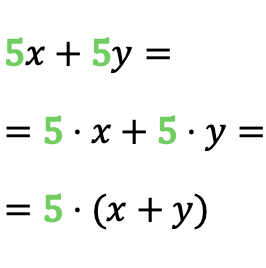
extraire ou supprimer le facteur commun d'un polynôme

Comme vous pouvez le voir dans l’exemple, le nombre 5 est répété dans le monôme 5x et dans le monôme 5y, donc le facteur commun du polynôme est 5. Ainsi, une fois que nous avons identifié le facteur commun, nous pouvons convertir la somme des monômes dans un produit.

N’oubliez pas de mettre les parenthèses lors de l’extraction du facteur commun, car le facteur commun doit multiplier tous les addends.

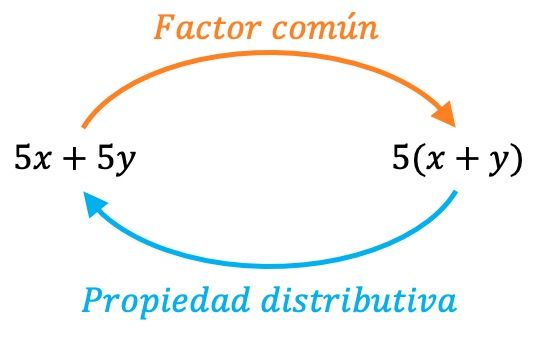
La suppression du facteur commun est l’opération inverse de la propriété distributive , c’est-à-dire qu’en réalité nous appliquons la propriété distributive à l’envers. Par conséquent, nous pouvons toujours vérifier que nous avons correctement extrait le facteur commun en effectuant le processus inverse :

Si en appliquant la propriété distributive nous obtenons le même polynôme depuis le début, cela signifie que nous avons obtenu correctement le facteur commun.
D’un autre côté, lorsque le résultat de l’utilisation de la propriété distributive est un autre polynôme différent du polynôme d’origine, cela implique que nous avons commis une erreur dans le processus d’extraction du facteur commun.

facteur commun et propriété distributive

Exemples de prise (ou d’extraction) de facteur commun

Nous vous laissons avec plus d’exemples pour finir de comprendre le concept de facteur commun :

Exemple 1

Comme vous le voyez dans cet exemple, un facteur commun peut être extrait de plus de deux termes en même temps :

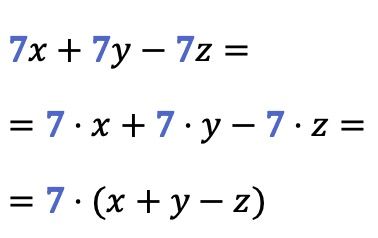
Exemple 2

Vous pouvez également extraire un facteur commun des variables (ou lettres) :

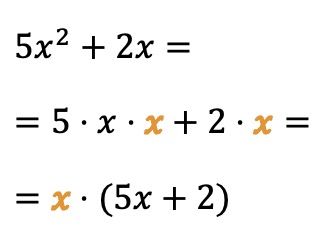
extraire le facteur commun dans les expressions algébriques

Dans ce cas, la lettre x multiplie les deux termes du polynôme, nous pouvons donc simplifier l’expression algébrique en prenant la variable x comme facteur commun.

Exemple 3

Dans cet exemple, le premier terme a la variable x élevée à la puissance 3 et dans le deuxième terme, le x est élevé à la puissance 2, de sorte que les deux termes ont deux x. Le facteur commun n’est donc pas seulement un x, mais x ² :

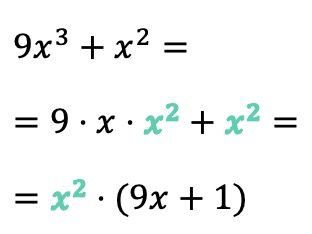
Par contre, remarquez que si le facteur commun du polynôme coïncide exactement avec un terme, lorsque nous extrayons le facteur commun, nous devons mettre un 1 à sa place . Sinon, si on ne mettait rien à la place, on n’obtiendrait pas une expression équivalente.

comment extraire ou trouver un facteur commun

Exemple 4

Parfois, le facteur commun n’est pas si évident et n’est pas visible directement, mais il s’agit plutôt d’un diviseur des coefficients des monômes. Par exemple, le facteur commun dans l’exemple suivant est 3, puisque la décomposition factorielle de 6 et 9 contient 3 :

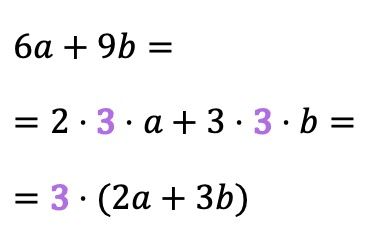
Ce type de facteur commun est appelé dans certains livres d’algèbre facteur commun maximum , puisque le facteur commun est en même temps le plus grand facteur commun (PGCD) des coefficients des termes polynomiaux.

Si vous êtes arrivé jusqu’ici, cela signifie que vous savez probablement déjà comment trouver le facteur commun d’un polynôme, parfait. Cependant, ne vous êtes-vous pas demandé à quoi sert le facteur commun ? Eh bien, une application du facteur commun est qu’il est utilisé pour factoriser des polynômes. Si vous ne savez toujours pas de quoi il s’agit, dans ce lien vous pouvez voir en quoi consiste la factorisation des polynômes et pourquoi le facteur commun est si important pour réaliser cette opération polynomiale.

Facteur commun aux fractions

Le facteur commun est également très utile pour simplifier des termes en fractions avec des polynômes au numérateur et au dénominateur.

Pour voir comment cela se fait, simplifions la fraction suivante à titre d’exemple :

$\cfrac{2x^2+4}{14x+8y}$

La première chose que nous devons faire est de trouver le facteur commun du polynôme numérateur et du polynôme dénominateur. Dans ce cas, le facteur commun des deux polynômes est 2 :

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

Extrayons maintenant le facteur commun des deux polynômes :

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

Et une fois que nous avons obtenu un facteur commun aux deux polynômes, nous devons supprimer les facteurs qui se répètent au numérateur et au dénominateur :

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

En conclusion, la fraction simplifiée est :

$\cfrac{x^2+2}{7x+4y}$

Facteur commun par regroupement

Une façon de réduire les termes d’un polynôme consiste à utiliser la méthode du facteur commun en regroupant les termes , également appelée extraction du double facteur commun. Comme son nom l’indique, cette procédure consiste à simplifier l’expression d’un polynôme en regroupant deux fois ses termes.

Cette méthode est un peu complexe, voyons donc comment elle est appliquée étape par étape avec le polynôme suivant :

$x^2+2x+5x+10$

Nous devons d’abord déterminer deux facteurs communs possibles différents, nous séparons donc le polynôme en deux parties :

$(x^2+2x)+(5x+10)$

Dans ce cas, les éléments x ² et 2x ont la lettre x comme facteur commun, et les termes 5x et 10 ont 5 comme facteur commun (puisque 10 est un multiple de 5). Nous avons donc ces deux facteurs en commun :

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

Et enfin, puisque les deux produits polynomiaux restants ont le facteur (x+2), nous pouvons simplifier le polynôme comme suit :

$(x+2)\cdot (x+5)$

Comme vous pouvez le constater, cette méthode n’est pas du tout facile. N’hésitez donc pas à nous poser toutes vos questions dans les commentaires, et nous y répondrons dans les plus brefs délais.

Exercices de facteurs communs résolus étape par étape

Nous vous laissons plusieurs exercices résolus étape par étape afin que vous puissiez vous entraîner à extraire le facteur commun d’un polynôme.

Exercice 1

Extrayez le facteur commun des polynômes suivants :

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

Voir la solution

A) Tous les termes qui composent le premier polynôme ont un 6, donc le facteur commun du polynôme est 6 :

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) Dans le deuxième polynôme, tous ses éléments ont au moins une lettre x. Voilà donc le facteur commun du polynôme :

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C) Le premier monôme du polynôme a évidemment un 2, et le deuxième monôme est un multiple de 2. Donc le facteur commun du polynôme est 2 :

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D) Dans le dernier polynôme toutes les variables sont au moins au carré. Le facteur commun est donc x ² :

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

Rappelons que lorsque le facteur commun est identique à un terme, il faut mettre un 1 à sa place.

Exercice 2

Prenons le facteur commun des polynômes suivants :

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

Voir la solution

A) Tous les coefficients des éléments qui composent le premier polynôme sont des multiples de 2, par conséquent, en extrayant le facteur commun le polynôme devient :

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B) Dans tous les termes du polynôme il y a au moins un x, donc :

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C) Le plus grand commun diviseur des coefficients de tous les termes du polynôme est 5, de sorte que le commun diviseur dudit polynôme est 5 :

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D) Tous les termes du polynôme ont au moins un x et, de plus, tous les coefficients sont des multiples de 3. Par conséquent, le facteur commun du polynôme est 3x :

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

Exercice 3

Trouvez le facteur commun de chacun des polynômes suivants et retirez-le :

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

Voir la solution

A) Tous les monômes ont au moins la lettre

$a$ au carré et la lettre $b$ au cube, donc le facteur commun est $a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B) Tous les coefficients du polynôme sont des multiples de 8 et, de plus, ils ont au minimum x ² et y ² comme partie littérale. Le facteur commun du polynôme est donc 8x ² y ² .

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C) Dans ce cas, le facteur commun coïncide avec la valeur du monôme intermédiaire

$\left(6ab^2c\right)$ , puisque les coefficients des autres monômes sont des multiples de $6$ et absolument tout le monde a $ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D) Dans ce cas particulier, le polynôme n’a pas de facteur commun, puisqu’aucun facteur n’est répété dans tous les termes du polynôme. Par conséquent, l’expression polynomiale ne peut pas être simplifiée algébriquement.

$18x^2y+10xy-5xy^3+4z$

Exercice 4

Simplifiez les fractions algébriques suivantes en prenant le facteur commun :

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

Voir la solution

La procédure pour simplifier une fraction algébrique, c’est-à-dire une fraction avec des polynômes, consiste à extraire le facteur commun du numérateur et du dénominateur de la fraction, puis à éliminer les facteurs qui se répètent au-dessus et au-dessous de la fraction. Donc:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

Exercice 5

Prenez le facteur commun des expressions polynomiales suivantes :

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

Voir la solution

A) Tous les termes du polynôme peuvent être décomposés factoriellement au tiers, donc :

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B) Le facteur commun du polynôme à l’intérieur de la racine est 4 mais, alors, on peut sortir le facteur commun en calculant sa racine carrée :

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C) Dans ce polynôme on peut appliquer le processus d’extraction du facteur commun en regroupant :

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D) Tous les coefficients fractionnaires du polynôme sont des multiples de moitié, donc le facteur commun du polynôme est ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

Qu’avez-vous pensé de l’explication ? Avez-vous apprécié? N’oubliez pas non plus que si vous avez des questions sur la façon dont est déterminé le facteur commun d’un polynôme ou si vous ne comprenez pas un exercice, vous pouvez toujours nous les poser dans les commentaires, et nous vous répondrons.

Extraire ou retirer le facteur commun

Quel est le facteur commun ?

Comment obtenir (ou extraire) le facteur commun

Exemples de prise (ou d’extraction) de facteur commun

Exemple 1

Exemple 2

Exemple 3

Exemple 4

Facteur commun aux fractions

Facteur commun par regroupement

Exercices de facteurs communs résolus étape par étape

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply