Sur cette page, nous expliquons comment appliquer la règle de Ruffini pour diviser des polynômes. En plus de l’explication, vous pourrez voir des exemples et des exercices résolus étape par étape sur les divisions de polynômes avec la règle de Ruffini. De plus, vous trouverez toutes les applications de cette méthode et, en fait, plus d’une vous surprendra sûrement.
Quelle est la règle de Ruffini ?
En mathématiques, la règle de Ruffini est une méthode algébrique qui permet de diviser rapidement n’importe quel polynôme par des polynômes de la forme xr . La règle de Ruffini doit son nom au mathématicien Paolo Ruffini, qui a inventé cette méthode.
Cependant, la règle de Ruffini n’est pas seulement utilisée pour diviser des polynômes, elle a bien d’autres utilisations. Par exemple, la règle de Ruffini est également utilisée pour trouver les racines d’un polynôme, pour trouver la valeur numérique d’un polynôme, pour factoriser un polynôme ou même pour résoudre des équations de troisième degré ou plus. Ci-dessous, nous verrons comment la règle de Ruffini est appliquée pour pouvoir effectuer toutes ces opérations.
Enfin, la règle de Ruffini est également connue sous le nom de méthode de Ruffini, théorème de Ruffini ou division synthétique de polynômes.
Comment appliquer la règle de Ruffini
Comme nous l’avons vu, l’utilité principale de la règle de Ruffini est de diviser un polynôme par un binôme, c’est-à-dire de faire une division du type suivant :
![]()
A noter que pour utiliser la règle de Ruffini , le polynôme diviseur doit toujours être formé par un x (avec un coefficient égal à 1) et un nombre (positif ou négatif), sinon l’algorithme de Ruffini ne peut pas être utilisé.
Pour appliquer la règle de Ruffini, toute une procédure doit être suivie, nous allons donc ci-dessous résoudre un exemple étape par étape pour voir comment la règle de Ruffini (ou la méthode de Ruffini) est appliquée.
Exemple de règle de Ruffini
- Résolvez la division de polynômes suivante en utilisant la règle de Ruffini :
![]()
Tout d’abord il faut tracer deux droites perpendiculaires se coupant, puis placer le dividende et le diviseur comme suit :
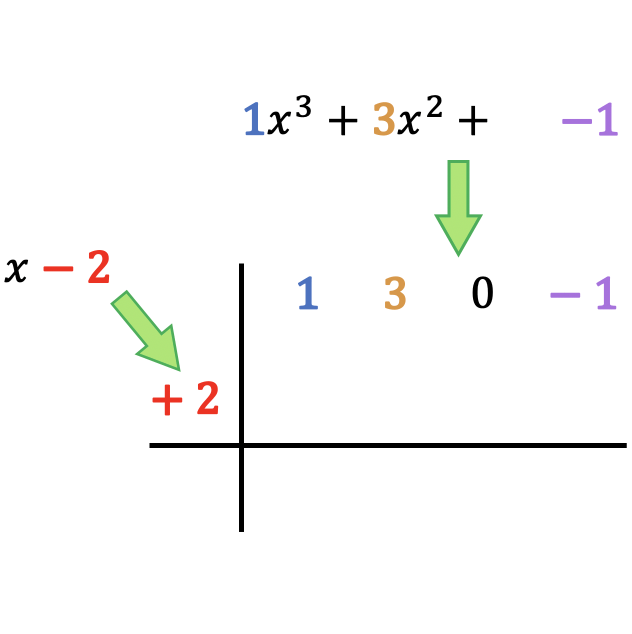
Comme vous pouvez le constater, il faut mettre les coefficients du polynôme dividende en haut, classés du degré le plus élevé au plus bas, et on place le terme indépendant du polynôme diviseur à gauche de la case avec un changement de signe .
Attention : Si le polynôme dividende n’a pas de terme d’un certain degré (polynôme incomplet), un 0 est mis à sa place. Par exemple, dans ce cas le polynôme
![]() Il n’a pas de monôme de degré 1, nous avons donc mis un 0 à sa place.
Il n’a pas de monôme de degré 1, nous avons donc mis un 0 à sa place.
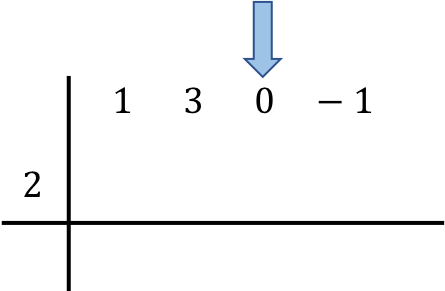
Une fois que l’on a positionné les polynômes impliqués dans l’opération, on abaisse le premier nombre directement à la ligne du dessous :
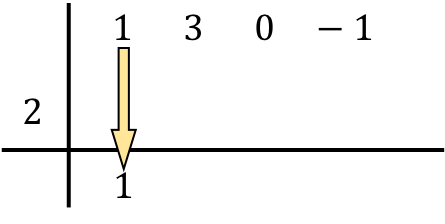
Vient maintenant l’étape qui caractérise la règle de Ruffini : on multiplie le nombre ci-dessous par le nombre de gauche et on place le résultat dans la colonne suivante :
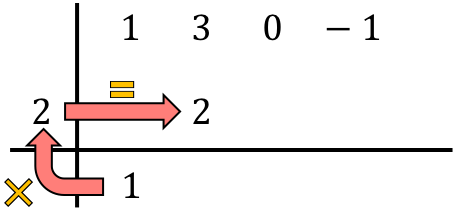
Et on additionne les nombres dans la colonne, en mettant le résultat de la somme juste en dessous :
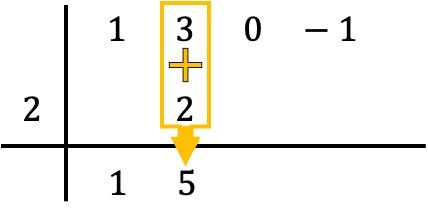
Ainsi, la méthode de Ruffini consiste à répéter ce processus. On refait donc la même chose : on multiplie le nombre du bas par le nombre de gauche, on met le résultat dans la colonne suivante et, enfin, on additionne les nombres qui sont alignés verticalement :
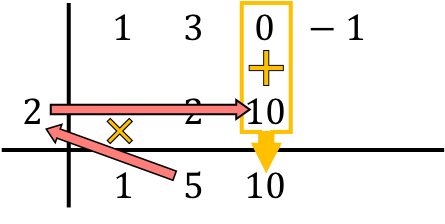
Et on répète la même procédure successivement jusqu’à la fin. On fait d’abord le produit du nombre ci-dessous par le nombre de gauche, puis on place le résultat dans la colonne suivante et, enfin, on additionne les nombres dans la même colonne :
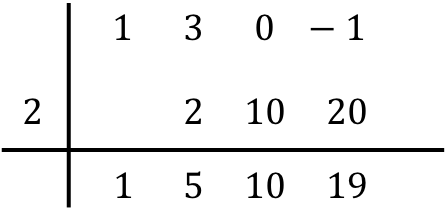
Ainsi, lorsque nous avons rempli toutes les colonnes, cela signifie que nous avons fini de diviser les polynômes.
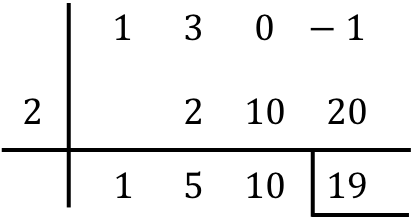
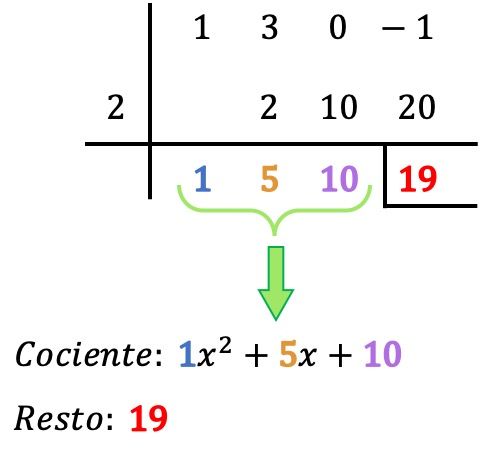
Il suffit donc de trouver le résultat de la division des polynômes :
- Le reste de la division entre les deux polynômes est le dernier nombre de la ligne ci-dessous, donc dans notre cas le reste est égal à 19. Le reste est généralement indiqué en plaçant une barre à gauche et une autre en dessous dudit nombre.
- Le quotient de la division polynomiale est déterminé par les autres valeurs obtenues, qui sont les coefficients du quotient polynomial. Le premier chiffre en partant de la droite correspond au coefficient du terme grade 0, le chiffre suivant est le coefficient du terme grade 1, le suivant au grade 2, le suivant au grade 3,… et ainsi de suite jusqu’à la fin. . Donc:
Exercices résolus de la règle de Ruffini
Ci-dessous vous trouverez plusieurs exercices résolus étape par étape sur la règle de Ruffini afin que vous puissiez vous entraîner et comprendre comment résoudre des divisions de polynômes avec cette méthode. Nous vous recommandons d’essayer chaque exercice puis de vérifier si vous l’avez fait correctement en regardant la correction.
Exercice 1
Effectuez la division suivante de polynômes avec la règle de Ruffini :
![]()
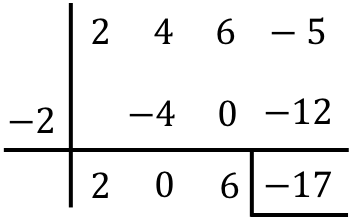
Le résultat de la division entre les deux polynômes est donc :
Quotient:
![]()
Repos:
![]()
Exercice 2
Calculez la division suivante de polynômes en utilisant la règle de Ruffini :
![]()
Dans ce cas particulier le polynôme dividende n’a pas de terme du deuxième degré, il faut donc mettre un zéro à sa place :
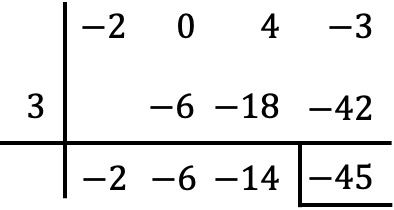
Le résultat de la division entre les 2 polynômes est donc :
Quotient:
![]()
Repos:
![]()
Exercice 3
Trouvez le résultat de la division suivante des polynômes par la règle de Ruffini :
![]()
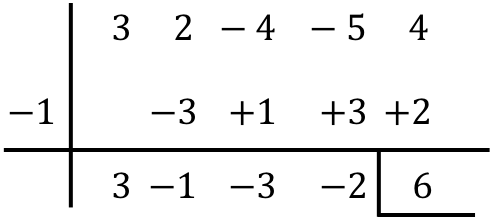
En conclusion, le résultat de la division des deux polynômes est :
Quotient:
![]()
Repos:
![]()
Exercice 4
Trouvez la valeur de l’inconnue m pour que le reste de la division suivante des polynômes soit équivalent à 5 :
![]()
Puisque le diviseur est de la forme (xr) ou (x+r), nous pouvons appliquer la règle de Ruffini pour résoudre la division. Nous appliquons donc la méthode de Ruffini en faisant glisser l’inconnu m :
Maintenant on égalise le reste obtenu à 5, car le reste doit être 5 :
![]()
Et on résout l’équation pour trouver la valeur du paramètre m :
![]()
![]()
Ainsi, lorsque la variable m est équivalente à 3, le reste de la division entre les polynômes sera égal à 5.
Exercice 5
Déterminer la valeur du paramètre m pour que le reste de la division polynomiale suivante donne 3 :
![]()
Puisque le diviseur est de la forme (xr) ou (x+r), nous pouvons appliquer la règle de Ruffini pour résoudre la division. Par conséquent, nous utilisons la méthode de Ruffini en faisant glisser l’inconnue m :
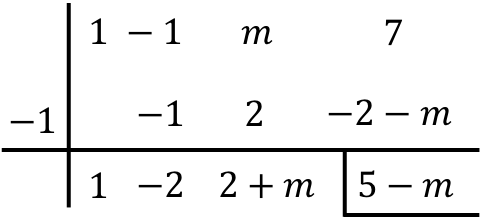
Gardez à l’esprit la propriété distributive lors de la dernière multiplication :
![]()
En revanche, le calcul du reste de la division est :
![]()
![]()
![]()
Nous égalisons maintenant l’expression du reste obtenue à 3, puisque le reste de la division doit être égal à 3 :
![]()
Et on résout l’équation résultante pour déterminer la valeur du paramètre m :
![]()
![]()
![]()
![]()
Par conséquent, m doit être égal à 2 pour que le reste de la division polynomiale soit égal à 3.
Plus d’applications de la règle de Ruffini
Comme expliqué, la règle de Ruffini est principalement utilisée pour effectuer une division entre polynômes. Cependant, la règle de Ruffini est également utilisée pour effectuer d’autres calculs, nous les verrons ci-dessous chacun d’entre eux.
Racines d’un polynôme
Les racines d’un polynôme peuvent être facilement déterminées à l’aide de la règle de Ruffini. Si vous ne savez pas quelle est la racine d’un polynôme, passons en revue sa définition :
Les racines (ou zéros) d’un polynôme sont les valeurs qui annulent le polynôme. Ou en d’autres termes, les racines d’un polynôme sont toutes ces valeurs qui, lorsqu’elles sont évaluées dans le polynôme, ont une valeur numérique égale à 0.
![]()
D’autre part, nous savons grâce au théorème des restes que si la valeur numérique d’un polynôme pour une valeur donnée
![]() est nul, nécessairement le reste de la division dudit polynôme entre
est nul, nécessairement le reste de la division dudit polynôme entre![]() Il doit également être 0.
Il doit également être 0.
![]()
Par conséquent, si vous utilisez la règle de Ruffini pour diviser un polynôme
![]() entre un autre polynôme de la forme
entre un autre polynôme de la forme![]() on obtient un reste égal à 0, cela veut dire que
on obtient un reste égal à 0, cela veut dire que![]() est une racine du polynôme
est une racine du polynôme![]()
Avec un exemple, on comprendra sûrement mieux :
- Vérifier si
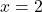 est une racine du polynôme
est une racine du polynôme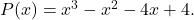
Pour vérifier si la valeur donnée est une racine du polynôme, il suffit d’appliquer la méthode de Ruffini avec ledit polynôme et ladite valeur :
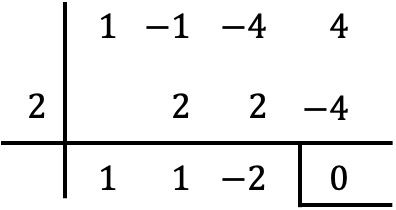
Puisque le reste obtenu par la règle de Ruffini est égal à zéro, cela signifie que effectivement
![]() est une racine du polynôme
est une racine du polynôme ![]()
Factorisation de polynômes
La règle de Ruffini est la méthode habituellement appliquée aux polynômes factoriels, car elle permet de connaître rapidement toutes les racines d’un polynôme de degré 3, 4, 5, etc.
Voyons donc comment factoriser un polynôme avec l’algorithme de Ruffini à l’aide d’un exemple :
- Factoriser le polynôme du troisième degré suivant :
![]()
La première chose à faire est de trouver toutes les racines du polynôme. Et les racines possibles d’un polynôme sont les diviseurs du terme indépendant, qui dans ce cas est 6. Donc :
Racines possibles du polynôme : +1, -1, +2, -2, +3, -3, +6, -6
Nous devons maintenant essayer de diviser le polynôme entre chacune de ces valeurs avec la règle de Ruffini. Si le reste de la division est égal à 0, cela signifie que la valeur est une racine du polynôme ; cependant, si le reste de la division est différent de 0, la valeur n’est pas une racine du polynôme. Ainsi, tester la règle de Ruffini avec tous les nombres n’annule le reste que dans les trois cas suivants :
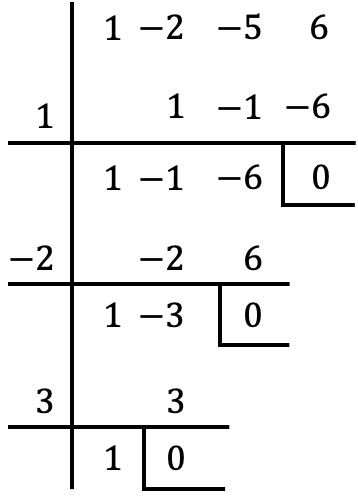
Par conséquent, les racines du polynôme du problème sont les valeurs avec lesquelles le reste s’annule, c’est-à-dire :
![]()
Enfin, pour factoriser le polynôme il faut exprimer chaque racine
![]() sous la forme d’un facteur du type
sous la forme d’un facteur du type![]() , c’est-à-dire que pour chaque racine il faut mettre une parenthèse avec un
, c’est-à-dire que pour chaque racine il faut mettre une parenthèse avec un![]() et la racine trouvée a changé de signe :
et la racine trouvée a changé de signe :
![]()
Comme vous pouvez le constater, nous avons réussi à décomposer le polynôme en facteurs en utilisant la règle de Ruffini. Cependant, vous avez peut-être eu des doutes sur la factorisation des polynômes, car il s’agit d’un sujet très complexe. Dans ce cas, vous pouvez rechercher sur notre site Web (dans le moteur de recherche en haut à droite) l’article que nous avons sur la façon de factoriser les polynômes , nous l’expliquons là plus en détail et vous pouvez vous entraîner avec des exercices résolus étape par étape. De plus, nous vous montrons également d’autres méthodes pour factoriser des polynômes.
Calculer la valeur numérique d’un polynôme
Bien que cela puisse paraître surprenant, la valeur numérique d’un polynôme peut être déterminée par la règle de Ruffini grâce au théorème des restes.
Mais évidemment, pour ce faire, vous devez connaître le théorème des restes. Si ce n’est pas le cas, vous pouvez rechercher l’explication du théorème des restes sur notre site internet (dans le moteur de recherche en haut à droite) .
Ainsi, grâce au théorème des restes, nous pouvons connaître la valeur numérique de n’importe quel polynôme. Voyons comment procéder à l’aide d’un exemple :
- Calculer la valeur numérique de
 pour
pour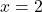 appliquant la règle de Ruffini, étant
appliquant la règle de Ruffini, étant 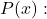
![]()
Pour trouver la valeur numérique du polynôme pour la valeur
![]() La seule chose que nous devons faire est d’utiliser la règle de Ruffini avec le polynôme et ladite valeur :
La seule chose que nous devons faire est d’utiliser la règle de Ruffini avec le polynôme et ladite valeur :
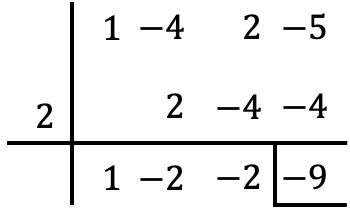
Ainsi, d’après le théorème des restes, nous savons que la valeur numérique du polynôme coïncide avec le reste de la division polynomiale . Par conséquent, la valeur numérique du polynôme dans
![]() est -9.
est -9.
![]()
En revanche, on peut vérifier que la règle de Ruffini est bien appliquée en calculant numériquement la valeur numérique :
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Résoudre des équations du troisième degré ou plus
Une autre application de la règle de Ruffini est de résoudre des équations de degré supérieur à 2, puisque dans ces cas il n’y a pas de formule comme dans l’équation du deuxième degré. Voyons comment procéder à l’aide d’un exemple :
- Résolvez l’équation du troisième degré suivante en utilisant la règle de Ruffini :
![]()
Nous devons traiter l’équation comme s’il s’agissait d’un polynôme. Ensuite, il faut calculer autant de racines du “polynôme” par la règle de Ruffini jusqu’à obtenir une équation du deuxième degré . Dans ce cas il s’agit d’une équation de degré 3, il suffit donc de déterminer une racine du « polynôme » :
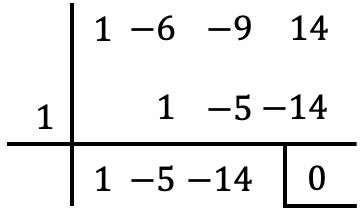
Une solution de l’équation sera donc
![]() Eh bien, pour trouver les autres solutions, il faut mettre le polynôme obtenu dans le quotient de la règle de Ruffini égal à 0 :
Eh bien, pour trouver les autres solutions, il faut mettre le polynôme obtenu dans le quotient de la règle de Ruffini égal à 0 :
![]()
Et maintenant, nous résolvons l’équation quadratique résultante avec sa formule correspondante :
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
En conclusion, les 3 solutions de l’équation du troisième degré sont :
![]()