Matrice orthogonale

Sur cette page, vous verrez ce que sont les matrices orthogonales et la relation qu’elles ont avec l’inverse d’une matrice. Vous verrez également plusieurs exemples pour le comprendre parfaitement. De plus, nous vous apprenons la formule qui vérifie n’importe quelle matrice orthogonale, avec laquelle vous saurez en trouver une rapidement. Et enfin, vous trouverez les propriétés et les applications de ces matrices particulières ainsi qu’un exercice typique d’examen résolu.

Qu’est-ce qu’une matrice orthogonale ?

La définition de matrice orthogonale est la suivante :

Une matrice orthogonale est une matrice carrée à nombres réels qui multipliée par sa transposée (ou transposition) est égale à la matrice d’identité. C’est-à-dire que la condition suivante est remplie :

$A\cdot A^t = A^t \cdot A =I$

Où

$A$ est une matrice orthogonale et $A^t$ représente sa matrice transposée.

Pour que cette condition soit remplie, les colonnes et les lignes d’une matrice orthogonale doivent être des vecteurs unitaires orthogonaux, c’est-à-dire qu’elles doivent former une base orthonormée. Pour cette raison, certains mathématiciens les appellent également matrices orthonormées .

Inverse d’une matrice orthogonale

Une autre façon d’expliquer le concept de matrice orthogonale est à travers la matrice inverse, car la matrice transposée (ou transposée) d’une matrice orthogonale est égale à son inverse.

Pour bien comprendre ce théorème, il est important que vous sachiez inverser une matrice . Dans ce lien, vous trouverez une explication détaillée de l’inverse d’une matrice, toutes ses propriétés et vous avez même des exercices résolus étape par étape pour vous entraîner.

La matrice inversée d’une matrice orthogonale peut facilement être montrée comme étant équivalente à sa transposée en utilisant la condition de matrice orthogonale et la propriété principale des matrices inverses :

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Par conséquent, une matrice orthogonale sera toujours une matrice inversible , ou en d’autres termes, ce sera une matrice régulière ou non dégénérée.

Ensuite, nous allons voir plusieurs exemples de matrices orthogonales pour finir de comprendre le concept de tout.

Exemple de matrice orthogonale 2×2

La matrice suivante est une matrice orthogonale de dimension 2×2 :

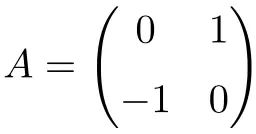
On peut vérifier qu’il est orthogonal en calculant le produit par sa transposée :

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Puisque le résultat donne la matrice Identique, on vérifie que A est une matrice orthogonale.

Exemple de matrice orthogonale 3×3

La matrice suivante est une matrice orthogonale de dimension 3×3 :

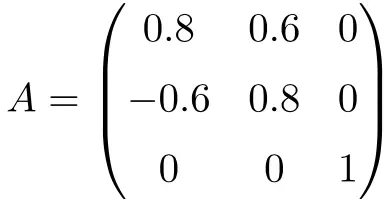
On peut montrer qu’elle est orthogonale en multipliant la matrice A par sa transposée :

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Puisque la solution est la matrice unitaire, on montre que A est une matrice orthogonale.

Formule pour trouver une matrice orthogonale 2×2

Nous allons voir ensuite la preuve que toutes les matrices orthogonales d’ordre 2 suivent le même schéma.

Soit une matrice générique de taille 2×2 :

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Pour que cette matrice soit orthogonale, l’équation matricielle suivante doit être satisfaite :

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

En résolvant la multiplication matricielle, on obtient les équations suivantes :

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Si vous regardez bien, ces égalités ressemblent beaucoup à la relation trigonométrique fondamentale de Pythagore :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Par conséquent, les termes satisfaisant aux équations (1) et (3) obtenus sont :

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

De plus, en substituant les valeurs dans la deuxième équation, nous obtenons la relation entre les deux angles :

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

C’est-à-dire que l’une des deux conditions suivantes doit être remplie :

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Donc, en conclusion, les matrices orthogonales doivent avoir la structure de l’une des deux matrices suivantes :

formule de la matrice orthogonale de dimension 2x2

Où

$\theta$ est un nombre réel.

En effet, si à titre d’exemple on accorde la valeur

$\displaystyle\theta=\frac{\pi}{2}$ et on prend la première structure, on obtiendra la matrice dont on a vérifié qu’elle était orthogonale dans la section « Exemple de matrice orthogonale 2×2 » :

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Propriétés de la matrice orthogonale

Les caractéristiques de ce type de matrice sont :

Une matrice orthogonale ne peut jamais être une matrice singulière , car elle peut toujours être inversée. En ce sens, l’inverse d’une matrice orthogonale est une autre matrice orthogonale.

Toute matrice orthogonale peut être diagonalisée. On dit alors que les matrices orthogonales sont diagonalisables orthogonalement.

Toutes les valeurs propres ou valeurs propres d’une matrice orthogonale ont un module égal à 1.

Toute matrice orthogonale composée uniquement de nombres réels est également une matrice normale.

L’analogue de la matrice orthogonale dans un environnement avec des nombres complexes est la matrice unitaire.

Évidemment, la matrice d’identité est une matrice orthogonale.

L’ensemble des matrices orthogonales de dimension n × n ainsi que l’opération du produit matriciel forment un groupe appelé groupe orthogonal. Autrement dit, le produit de deux matrices orthogonales est égal à une autre matrice orthogonale.

De plus, le résultat de la multiplication d’une matrice orthogonale par sa transposée peut être exprimé par le delta de Kronecker :

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Enfin, le déterminant d’une matrice orthogonale vaut toujours +1 ou -1.

$\displaystyle \text{det}(A)=\pm 1$

Exercice résolu de matrices orthogonales

Nous allons ensuite résoudre un exercice sur les matrices orthogonales.

Étant donné la matrice carrée d’ordre 3 suivante, trouver les valeurs de $a$ et $b$ pour le rendre orthogonal :

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Pour que l’orthogonalité de la matrice soit remplie, il faut que le produit de la matrice par sa transposée soit égal à la matrice d’Identité. Donc:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

On fait la multiplication des matrices :

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Nous pouvons maintenant obtenir une équation du coin supérieur gauche des matrices, car les éléments situés à cette position doivent correspondre. Pourtant:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Nous résolvons l’équation et éliminons l’inconnue :

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Cependant, il y a des équations qui ne tiennent pas avec la solution positive, par exemple celle dans le coin supérieur droit. Donc seule la solution négative est réalisable .

D’autre part, pour calculer la variable

$b$ nous pouvons faire correspondre, par exemple, les termes placés dans la deuxième ligne de la première colonne :

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

En remplaçant la valeur de

$a$ dans l’équation :

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Bref, la seule solution possible est :

$\displaystyle \bm{a=b =-2}$

Donc la matrice orthogonale qui correspond à ces valeurs est :

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Applications des matrices orthogonales

Bien que cela puisse ne pas sembler être le cas car elles ont généralement une forme très simple, les matrices orthogonales sont très importantes en mathématiques, en particulier dans le domaine de l’algèbre linéaire.

En géométrie, les matrices orthogonales représentent des transformations isométriques (qui ne changent pas les distances et les angles) dans des espaces vectoriels réels, c’est pourquoi elles sont appelées transformations orthogonales. De plus, ces transformations sont des isomorphismes internes de l’espace vectoriel considéré. Ces transformations peuvent être des rotations , des réflexions spéculaires ou des inversions .

Enfin, ce type de matrice est également utilisé en physique, puisqu’il permet d’étudier le mouvement des corps rigides. Et ils sont même utilisés dans la formulation de certaines théories des champs.