Dans cette page vous trouverez l’explication d’une matrice régulière ou inversible et comment savoir quand l’inversion d’une matrice peut être effectuée et quand non. De plus, vous verrez également plusieurs exemples de matrices régulières pour bien comprendre le concept et, enfin, nous vous montrerons toutes les propriétés de ce type de matrice.
Qu’est-ce qu’une matrice régulière ?
La définition d’une matrice régulière est la suivante :
Une matrice régulière est une matrice carrée qui peut être inversée, c’est-à-dire que l’inverse de ladite matrice peut être calculé. Par conséquent, son déterminant est différent de zéro (0).
Les matrices régulières sont également appelées matrices inversibles, non singulières ou non dégénérées .
La matrice opposée à la matrice régulière est la matrice singulière ou dégénérée.
Ainsi, pour savoir quand une matrice est régulière ou singulière, c’est-à-dire quand une matrice est inversible ou non, il suffit de résoudre le déterminant de la matrice :
- Si le déterminant de la matrice est non nul, la matrice est régulière ou inversible.
- Si le déterminant de la matrice est égal à zéro, la matrice est singulière ou non inversible.
En conclusion, calculer le déterminant d’une matrice est le moyen le plus simple de savoir si la matrice a un inverse ou non, c’est donc ce que nous recommandons pour déterminer l’inversibilité de toute matrice.
Si vous voulez savoir comment inverser une matrice, vous pouvez consulter la formule de la matrice inverse , qui explique pas à pas comment inverser une matrice, et vous trouverez également plusieurs exemples et exercices résolus pour vous entraîner.
Exemples de matrices régulières ou inversibles
Une fois que nous avons vu la signification de matrice régulière ou inversible, voyons quelques exemples de matrices régulières de différentes dimensions :
Exemple de matrice 2×2 régulière ou inversible
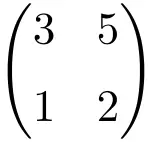
On peut vérifier qu’il s’agit d’une matrice régulière en calculant son déterminant :
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e4a833393b2e66b49eb3b434136b755_l3.png)
Le déterminant de la matrice d’ordre 2 est différent de 0, c’est donc une matrice régulière.
Exemple de matrice 3×3 régulière ou inversible
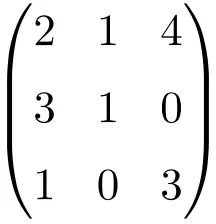
Il faut faire le déterminant de la matrice pour vérifier qu’il s’agit d’une matrice inversible :
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0389d86d007f9ee667b14c0071b6395_l3.png)
Le déterminant de la matrice d’ordre 3 donne un résultat autre que 0, donc c’est une matrice régulière.
Exemple de matrice 4×4 régulière ou inversible

Prendre le déterminant de la matrice montre qu’il s’agit d’une matrice régulière :
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a07b3fa1ed83267c0bc723dd027d724_l3.png)
Le déterminant de la matrice d’ordre 4 n’est pas nul, c’est donc une matrice inversible.
Attention : Si vous avez des doutes sur les calculs des déterminants, vous pouvez consulter la page comment calculer un déterminant .
Propriétés des matrices régulières ou inversibles
Les matrices régulières ou inversibles sont très importantes pour l’algèbre linéaire, et cela est dû aux caractéristiques suivantes :
- Si A est une matrice inversible, sa matrice transposée ou transposée l’est aussi. De plus, la matrice inverse de la transposition est égale à la transposition de l’inverse.
![]()
- La plage d’une matrice régulière est toujours le maximum possible, ou en d’autres termes, la plage est équivalente à la dimension de la matrice.
- Le produit matriciel entre deux matrices inversibles donne naissance à une autre matrice régulière. Cette condition peut être facilement démontrée avec les propriétés des déterminants :
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-88d940d46390d4f5f0d6e694ac5a18d5_l3.png)
- Toute matrice orthogonale est en même temps une matrice régulière.
- Soit A la matrice qui représente un système d’équations linéaires
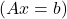 , si A est une matrice régulière, le système a une solution unique, c’est donc un système déterminant compatible (SCD).
, si A est une matrice régulière, le système a une solution unique, c’est donc un système déterminant compatible (SCD).
- De plus, si le système est un système homogène
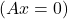 et A peut s’inverser, la solution du système est triviale :
et A peut s’inverser, la solution du système est triviale :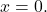
- Les colonnes et les lignes d’une matrice régulière sont linéairement indépendantes les unes des autres.
- Toutes les valeurs propres (ou valeurs propres) d’une matrice régulière ou inversible sont non nulles.