Sur cette page vous apprendrez ce que c’est et comment calculer l’inverse d’une matrice par la méthode des déterminants (ou matrice adjointe) et par la méthode de Gauss. Vous verrez également toutes les propriétés de la matrice inverse, et vous trouverez également des exemples et des exercices résolus étape par étape pour chaque méthode afin que vous les compreniez parfaitement. Enfin, nous expliquons une formule pour inverser rapidement une matrice 2×2 et même la plus grande utilité de cette opération matricielle : résoudre un système d’équations linéaires.
Quel est l’inverse d’une matrice ?
Être
![]() une matrice carrée. La matrice inverse de
une matrice carrée. La matrice inverse de![]() ça s’écrit
ça s’écrit![]() , et c’est cette matrice qui satisfait :
, et c’est cette matrice qui satisfait :
![]()
![]()
Où
![]() est la matrice Identité.
est la matrice Identité.
Quand peut-on inverser une matrice et quand ne le peut-on pas ?
Le moyen le plus simple de déterminer l’inversibilité d’une matrice consiste à utiliser son déterminant :
- Si le déterminant de la matrice en question est différent de 0, cela signifie que la matrice est inversible. Dans ce cas on dit que c’est une matrice régulière. De plus, cela implique que la matrice est de rang maximum.
- En revanche, si le déterminant de la matrice est égal à 0, la matrice ne peut pas être inversée. Et, dans ce cas, on dit qu’il s’agit d’une matrice singulière ou dégénérée.
Principalement, il existe deux méthodes pour inverser n’importe quelle matrice : la méthode des déterminants ou matrice adjointe et la méthode de Gauss. Ci-dessous vous avez l’explication du premier, mais vous pouvez également consulter ci-dessous comment inverser une matrice avec la méthode de Gauss.
Inverser une matrice par la méthode des déterminants (ou par la matrice adjacente)
Pour calculer l’ inverse d’une matrice ,
![]() , la formule suivante doit être appliquée :
, la formule suivante doit être appliquée :
![]()
Où:
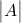 est le déterminant de la matrice
est le déterminant de la matrice
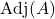 est la matrice adjointe de
est la matrice adjointe de
- L’exposant
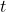 indique la transposition de la matrice, c’est-à-dire que la matrice attachée doit être transposée.
indique la transposition de la matrice, c’est-à-dire que la matrice attachée doit être transposée.
Commentaire : Certains livres utilisent une formule matricielle inverse légèrement différente : ils transposent d’abord la matrice A puis calculent sa matrice adjointe, au lieu de calculer d’abord la matrice adjointe puis de la transposer. En réalité, l’ordre n’a pas d’importance car le résultat est exactement le même. Nous vous laissons ici la formule pour inverser une matrice modifiée au cas où vous préféreriez utiliser celle-ci :

Nous allons ensuite voir comment trouver l’inverse d’une matrice en résolvant un exercice à titre d’exemple :
Exemple de calcul de la matrice inverse par la méthode des déterminants (ou matrice adjointe) :
- Calculez l’inverse de la matrice suivante :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
Pour déterminer l’inverse de la matrice, il faut appliquer la formule suivante :
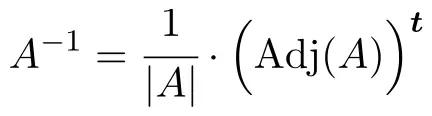
Mais si le déterminant de la matrice est nul cela signifie que la matrice n’est pas inversible. Par conséquent, la première chose à faire est de calculer le déterminant de la matrice et de vérifier qu’il est différent de 0 :
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2](https://mathority.org/wp-content/ql-cache/quicklatex.com-710ccd4e4912dd492b496a742eaf7f56_l3.png)
Le déterminant n’est pas 0 , donc la matrice est inversible .
Par conséquent, en substituant la valeur du déterminant dans la formule, l’inverse de la matrice sera :
![]()
![]()
Il faut maintenant calculer la matrice adjointe de A. Pour ce faire, il faut remplacer chaque élément de la matrice A par son adjoint.
N’oubliez pas que pour calculer l’ attachement de
![]() , c’est-à-dire de l’élément row
, c’est-à-dire de l’élément row![]() et de la colonne
et de la colonne![]() , la formule suivante doit être appliquée :
, la formule suivante doit être appliquée :
![]()
Où le mineur complémentaire de
![]() est le déterminant de la matrice éliminant la ligne
est le déterminant de la matrice éliminant la ligne![]() et la colonne
et la colonne![]() .
.
Ainsi, les adjoints des éléments de la matrice A sont :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
![]()
![]()
![]()
![]()
Commentaire : Ne confondez pas le déterminant 1×1 avec la valeur absolue, car dans le déterminant 1×1 le nombre n’est pas converti en positif.
Une fois les adjoints calculés, il suffit de remplacer les éléments de A par leurs adjoints pour trouver la matrice adjointe de A :
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08fb7666b4518399c2a469ba445762be_l3.png)
Commentaire : à certains endroits la matrice adjointe est la transposée de la matrice adjointe que nous avons définie ici.
Par conséquent, nous substituons la matrice ci-jointe dans la formule matricielle inverse et elle devient :
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0abb4127db9c3c1d0a7b669fbc782605_l3.png)
L’exposant
![]() Cela nous dit qu’il faut transposer la matrice . Et pour transposer une matrice il faut changer ses lignes en colonnes , c’est-à-dire que la première ligne de la matrice devient la première colonne de la matrice, et la deuxième ligne devient la deuxième colonne :
Cela nous dit qu’il faut transposer la matrice . Et pour transposer une matrice il faut changer ses lignes en colonnes , c’est-à-dire que la première ligne de la matrice devient la première colonne de la matrice, et la deuxième ligne devient la deuxième colonne :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22965912cf8aee99610c81cf575c0ecd_l3.png)
Et enfin, on multiplie chaque terme de la matrice par
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-220748840151b429919c7ce6587b1bc0_l3.png)
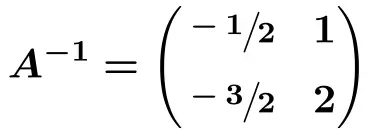
Exercices résolus sur les matrices inverses avec la méthode des déterminants (ou la matrice attenante)
Exercice 1
Inversez la matrice suivante de dimension 2×2 par la méthode de la matrice adjointe :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfb0807249e78845b375a402eb23a32b_l3.png)
La formule matricielle inverse est :
![]()
On calcule d’abord le déterminant de la matrice :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c4e3bac90eb0da0361b4be1a2225146_l3.png)
Le déterminant est différent de 0, donc la matrice peut être inversée.
Calculons maintenant la matrice adjointe de A :
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dea8fca2c025ff9b7d7673904344996_l3.png)
Une fois le déterminant de la matrice et son adjoint calculés, on substitue leurs valeurs dans la formule :
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9475e4162eff7e1ed9c08f363a8279ec_l3.png)
On transpose la matrice ci-jointe :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a6aaa8168e55c6eab1e3be1229a3da_l3.png)
La matrice inverse de A est donc :
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1236ad7262705dbbd9b0a094084ceac5_l3.png)
Exercice 2
Inversez la matrice carrée suivante par la méthode des déterminants :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb735917d200ed35918cd44be6bd155b_l3.png)
La formule matricielle inverse est :
![]()
On calcule d’abord le déterminant de la matrice :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-49cd3daf7c50c811e78c29efe036bda4_l3.png)
Le déterminant est différent de 0, donc la matrice peut être inversée.
Calculons maintenant la matrice adjointe de A :
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-208ab7161076485ca6928bd1208f6714_l3.png)
Une fois le déterminant de la matrice et son adjoint trouvés, on substitue leurs valeurs dans la formule :
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-babecc87455bdc54006a77ba5369e540_l3.png)
On transpose la matrice ci-jointe :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17529597656a112a27d136ca212834d8_l3.png)
On multiplie chaque élément par
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be52d2df839244cbb0b0ee00c9e45265_l3.png)
La matrice inverse de A est donc :
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13e218c7d075daba3f875345f324d001_l3.png)
Exercice 3
Inversez la matrice suivante de dimension 3×3 par la méthode de la matrice adjointe :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b6a5f638281754d80983b5a50e15be_l3.png)
La formule matricielle inverse est :
![]()
Nous résolvons d’abord le déterminant de la matrice avec la règle de Sarrus :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcac1cb3935b1000b6493a2866e8728a_l3.png)
Le déterminant est différent de 0, donc la matrice peut être inversée.
Une fois le déterminant résolu, on trouve la matrice adjointe de A :
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c510482ac77a8c5d511c095de600f1ba_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa99e03d34c925098c1ad3ed6f06c745_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bf9f8565b3e4a99ff254c7558699c13_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-99e2c3f55fbba7b5faa014758b60f4a8_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23326bccecf752508e7418cbbc8eacd3_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9d056af07ce26751783152a67cdedb6_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bed501806c35c94e491ad2063b2d0653_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f108a61eec662b9420708f6920060be_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77a152a00dbb5f1e0f8702dd9511095a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4642a75697fd30286065cdb4063a7bd_l3.png)
Une fois que l’on a calculé le déterminant de la matrice et son adjoint, on substitue leurs valeurs dans la formule :
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fae003a07d40b69690566cde77857c3a_l3.png)
On transpose la matrice ci-jointe :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55717407766afe98f50ca75f20536edc_l3.png)
Et la matrice inversée A est :
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9835713a5b791ee959d6571d706180f3_l3.png)
Exercice 4
Inversez la matrice d’ordre 3 suivante par la méthode de la matrice adjointe :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf71320b51e9514d1c372389aeb3410a_l3.png)
La formule matricielle inverse est :
![]()
Nous devons d’abord calculer le déterminant de la matrice, car si le déterminant est 0, cela signifie que la matrice n’a pas d’inverse.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb7dc647f4121450eeadf2f5b62b4475_l3.png)
Le déterminant de A est 0, la matrice ne peut donc pas être inversée.
Exercice 5
Inversez la matrice carrée 3 × 3 suivante par la méthode de la matrice des déterminants :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92e56e0f8013b6b65c0894a139537cae_l3.png)
La formule matricielle inverse est :
![]()
Tout d’abord on résout le déterminant de la matrice avec la règle de Sarrus :
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-07f116ed906c31644ed0513667988e6f_l3.png)
Le déterminant est différent de 0, donc la matrice peut être inversée.
Une fois le déterminant résolu, on trouve la matrice adjointe de A :
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-20da2eac0d49b1134b39b1f5c95c5659_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5b80624f0963dfb1a111d96b4e1ceae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50dd371e77d1896adb197321b68efd1d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60b779f4366a3ef38ae522fcfca8e7d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51cb00c42e6932810a4220eb85c61acd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b26cbfa55d5567d2dae10c5dfbd158_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d9f1bf4f5e01df910cd59bd4b25f816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ce129b17734facf076e48fb1928d0e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c8b319461dad7880bf2b9f20187b6fb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-748fcb9d9d2a8326379da4d2bd08534a_l3.png)
Une fois que l’on a calculé le déterminant de la matrice et son adjoint, on substitue leurs valeurs dans la formule :
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a0fc0e6effb520e22ff82c3034b4d4c_l3.png)
On transpose la matrice ci-jointe :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bba6ddbc8ab9f2c64eb03cdb9fea530a_l3.png)
Et enfin, nous opérons :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f999c23e7d5ce129b410b9f486983e_l3.png)
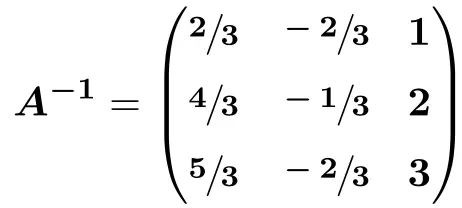
Inverser une matrice par la méthode de Gauss :
Pour calculer l’inverse d’une matrice avec la méthode de Gauss , il faut effectuer des opérations sur les lignes d’une matrice (nous le verrons plus loin). Alors avant de voir comment utiliser la méthode de Gauss, il est important que vous connaissiez toutes les opérations que l’on peut faire sur les lignes des matrices :
Transformations de lignes autorisées dans la méthode de Gauss
- Changez l’ordre des lignes de la matrice.
Par exemple, on peut changer l’ordre des lignes 2 et 3 d’une matrice :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d3f607625afb96bfb250168bd330818_l3.png)
- Multipliez ou divisez tous les termes d’une ligne par un nombre autre que 0.
Par exemple, nous pouvons multiplier la ligne 1 par 4 et diviser la ligne 3 par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cca4df71c23b1f005068a0a93b77dfe_l3.png)
- Remplacez une ligne par la somme de la même ligne plus une autre ligne multipliée par un nombre.
Par exemple, dans la matrice suivante, nous ajoutons la ligne 3 multipliée par 1 à la ligne 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ca6644f015dd42ddbf4ab159bd10dec_l3.png)
Exemple de calcul de la matrice inverse par la méthode de Gauss :
Voyons avec un exemple comment appliquer la méthode de Gauss pour inverser une matrice :
- Calculez l’inverse de la matrice suivante :
![Rendered by QuickLaTeX.com \displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-71553480cefa679dcb8eb98d97e0c717_l3.png)
La première chose que nous devons faire est de regrouper la matrice A et la matrice Identité en une seule matrice . La matrice A à gauche et la matrice Identité à droite :
![]()
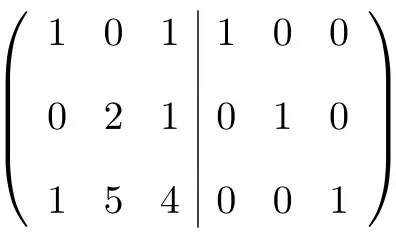
Pour calculer la matrice inverse, nous devons convertir la matrice de gauche en matrice identité. Et, pour ce faire, nous devons appliquer des transformations aux lignes jusqu’à ce que nous y parvenions.
Nous procéderons par colonnes, c’est-à-dire que nous effectuerons des opérations sur les lignes pour transformer d’abord les nombres de la première colonne, puis ceux de la deuxième colonne, et enfin ceux de la troisième colonne.
Les 1 et 0 dans la première colonne conviennent déjà, puisque la matrice d’identité a également un 1 et un 0 à ces positions. Par conséquent, il n’est pas nécessaire d’appliquer une transformation à ces lignes pour le moment.
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f51b3a869dde9c1697be9e57fce1548_l3.png)
Cependant, la matrice identité a un 0 dans le dernier élément de la première colonne, là où nous avons maintenant un 1. Il faut donc convertir le 1 en 0. Pour ce faire, on ajoute la ligne 1 multipliée par – à la ligne 3. 1:

Donc si on fait cette somme on se retrouve avec la matrice suivante :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-992a31603c2182a97d31ddf787df4f06_l3.png)
Nous avons ainsi réussi à transformer le 1 en 0.
Passons maintenant à la deuxième colonne de la matrice de gauche. Le premier élément est un 0, ce qui est bien car la matrice d’identité a un 0 à cette même position. Cependant, au lieu d’un 2, il devrait y avoir un 1, nous divisons donc la deuxième ligne par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a86b61ee601f9cd0ff9a70d1a280f887_l3.png)
De plus, dans la deuxième colonne, nous devons également transformer le 5 en 0. Eh bien, comme le 5 est cinq fois plus grand que le 1 dans la deuxième ligne, nous ajouterons la ligne 2 multipliée par -5 à la ligne 3 :

Par conséquent, en effectuant cette opération, nous nous retrouvons avec la matrice avec un 0 dans le dernier élément de la deuxième colonne :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcc790f05d73d308cb7d992841ab031a_l3.png)
Enfin, nous allons transformer la dernière colonne de la matrice à gauche, mais cette fois il faut commencer par le bas. Il faut donc transformer le
![]() en un 1. Par conséquent, nous multiplions la dernière ligne par 2 :
en un 1. Par conséquent, nous multiplions la dernière ligne par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-69614cae4dd388b6454ffd9b8d63c9a5_l3.png)
Il faut maintenant transformer le
![]() reste de la dernière colonne en 0. Cependant, cette fois, nous ne pouvons pas multiplier la ligne par 2, car nous convertirions également le 1 en 2 (lorsque la matrice d’identité a un 1 à cette position). Par conséquent, nous ajouterons la ligne 3 divisée par -2 à la ligne 2 :
reste de la dernière colonne en 0. Cependant, cette fois, nous ne pouvons pas multiplier la ligne par 2, car nous convertirions également le 1 en 2 (lorsque la matrice d’identité a un 1 à cette position). Par conséquent, nous ajouterons la ligne 3 divisée par -2 à la ligne 2 :

Donc en faisant cette opération on arrive à transformer le
![]() dans un 0 :
dans un 0 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-537958a51f67c7602ef121fa2c997ca8_l3.png)
Finalement, il suffit de transformer le 1 de la première ligne de la troisième colonne en 0. La troisième ligne a également un 1 dans cette même colonne, nous ajouterons donc la ligne 3 multipliée par -1 à la ligne 1 :
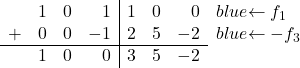
Et en faisant cette opération on arrive à convertir le 1 en un 0 :
![Rendered by QuickLaTeX.com \ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ddd39df6bc92258ba163c65de4fd59f_l3.png)
Une fois que l’on a réussi à convertir la matrice de gauche en matrice identité, on connaît aussi la matrice inverse. Parce que la matrice inverse est la matrice que l’on obtient du côté droit en convertissant la matrice de gauche en matrice identité . L’inverse de la matrice est donc :
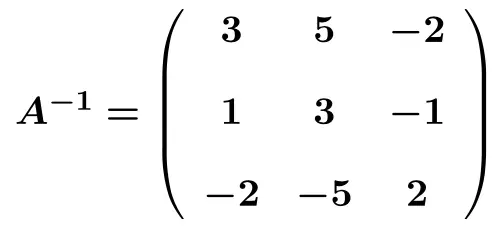
Exercices résolus sur les matrices inverses avec la méthode de Gauss
Exercice 1
Inversez la matrice suivante via la méthode de Gauss :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36886e1ab1007f9a53bdc0dd71a0d15b_l3.png)
La première chose que nous devons faire est de regrouper la matrice A et la matrice Identité dans une seule matrice. La matrice A à gauche et la matrice identité à droite :
![]()
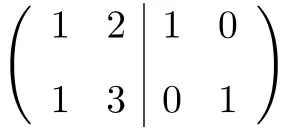
Maintenant, pour calculer la matrice inverse, nous devons convertir la matrice du côté gauche en matrice identité. Et, pour ce faire, nous devons appliquer des transformations aux lignes jusqu’à ce que nous y parvenions.
Le premier terme de tous, 1, est déjà le même que la matrice identité. Par conséquent, il n’est pas nécessaire d’appliquer une transformation à la première ligne pour le moment.
Cependant, la matrice identité a un 0 dans le dernier élément de la première colonne, là où nous avons maintenant un 1. Il faut donc convertir le 1 en 0. Pour ce faire, on soustrait la ligne 1 de la ligne 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-247d8605795c43e79b5d7742854cfe6d_l3.png)
On passe à la deuxième colonne : le 1 ci-dessous est bien. Mais pas le 2 ci-dessus, puisque la matrice identité a un 0 à cette position. Par conséquent, pour convertir le 2 en 0, de la ligne 1, nous soustrayons la ligne 2 multipliée par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-173a7bdb55ba058e5ae16d1fd8e91564_l3.png)
La matrice inverse est la matrice que l’on obtient du côté droit après avoir converti la matrice de gauche en matrice identité. Et maintenant nous avons obtenu la matrice d’identité sur le côté gauche. La matrice inverse est donc :
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98896d28465c9e1402e1c443375d93fe_l3.png)
Exercice 2
Inversez la matrice suivante avec la procédure gaussienne :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ae5ba4a92a5ddc00ddf5b11775edafd_l3.png)
Tout d’abord, nous mettons la matrice A et la matrice Identité dans une seule matrice :
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-81db2ef94d2db597cebb4c0c77685526_l3.png)
Nous devons maintenant transformer les lignes jusqu’à ce que nous convertissions la matrice de gauche en matrice d’identité.
La première colonne de la matrice de gauche est déjà la même que la première colonne de la matrice d’identité. Il n’est donc pas nécessaire de modifier aucun de ses numéros.
Cependant, la matrice identité a un 1 dans le deuxième élément de la deuxième colonne, où il y a maintenant un 3. Il faut donc convertir le 3 en un 1. Pour ce faire, de la ligne 2 on soustrait la ligne 3 multipliée par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd7cb4d4b81a75038807eb28393a83e_l3.png)
La matrice identité a un 0 dans le dernier élément de la deuxième colonne, où se trouve désormais un 1. Il faut donc convertir le 1 en 0. Pour ce faire, on soustrait la ligne 2 de la ligne 3 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-932479e2f574c19ad7906d3d20e52ad0_l3.png)
La matrice identité a un 0 dans le premier élément de la deuxième colonne, où il y a maintenant un 1. Il faut donc convertir le 1 en 0. Pour ce faire, on soustrait la ligne 2 de la ligne 1 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-566e1453aab03f9792cb281e4c88a68c_l3.png)
Il ne nous reste plus qu’à convertir le -4 en 0. Pour ce faire, on ajoute la ligne 3 multipliée par 4 à la ligne 1 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f98a9cabeb101602dd11aa73516b998_l3.png)
Nous avons déjà obtenu la matrice d’identité du côté gauche. La matrice inverse est donc :
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e43ce6a7061f0339bd5d44b83afec07f_l3.png)
Exercice 3
Inversez la matrice suivante par la méthode de Gauss :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f02b0186690e68baaa9a630db2c870db_l3.png)
Avant de commencer à opérer, nous devons mettre la matrice A et la matrice Identité en une seule matrice :
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa6dc5af82076e22b1d0cf7ea16d748b_l3.png)
Il faut maintenant convertir la matrice de gauche en matrice identité en opérant sur les lignes.
Les deux premiers éléments de la première colonne sont déjà les mêmes que ceux de la matrice identité. Il n’est donc pas nécessaire de modifier ces chiffres.
Mais la matrice identité a un 0 dans le troisième élément de la première colonne, où il y a maintenant un 2. Il faut donc convertir le 2 en un 0. Pour ce faire, de la ligne 3 on soustrait la ligne 1 multipliée par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-680a314b8cc900e01886291af12145e4_l3.png)
La matrice identité a un 0 dans le premier élément de la deuxième colonne, où il y a maintenant un 2. Il faut donc convertir le 2 en un 0. Pour ce faire, de la ligne 1 on soustrait la ligne 2 multipliée par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f87cbc594287f7ea4938091878562b4c_l3.png)
La matrice identité a un 0 dans le dernier élément de la deuxième colonne, où il y a maintenant un -4. Il faut donc convertir le -4 en 0. Pour cela, on ajoute la ligne 2 multipliée par 4 à la ligne 3 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8cf2c3878d2d35656953a55bb3baf94_l3.png)
Il ne nous reste plus qu’à convertir le premier élément de la troisième colonne en 0. Pour ce faire, on ajoute la ligne 3 multipliée par -1 à la ligne 1 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac851b05c2dc25af3d7b9ecc622c9f6_l3.png)
Nous avons déjà réalisé que la matrice de gauche est la matrice identité. Donc l’inverse de la matrice
![]() est:
est:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-161fbe4a4d4dcc4fc503b6e3a9e0bfeb_l3.png)
Exercice 4
Inversez la matrice suivante par la méthode de Gauss :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ad7ccd6aafab72255c96f2bc9148a2_l3.png)
La première chose que nous devons faire est de joindre la matrice A et la matrice Identité en une seule matrice :
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a832ceb9f09dfa88238c570b46b74d92_l3.png)
Il faut maintenant convertir la matrice du côté gauche en matrice identité en appliquant des opérations sur les lignes.
Le premier élément de la première colonne est déjà le même que celui de la matrice identité. Il n’est donc pas nécessaire de le changer.
Cependant, la matrice identité a un 0 dans le deuxième élément de la première colonne, où se trouve désormais un 1. Il faut donc convertir le 1 en 0. Pour cela, on soustrait la ligne 1 de la ligne 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83933b5a2315a4dcbc770bf92bf3831b_l3.png)
On passe à la deuxième colonne : on transforme d’abord le 4 en un 1 en divisant la deuxième ligne par 4 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-298984c72a249e2b5c98740cc0c1a11e_l3.png)
La matrice identité a un 0 dans le premier élément de la deuxième colonne, où il y a maintenant un -2. Il faut donc convertir -2 en 0. Pour ce faire, on ajoute la ligne 2 multipliée par 2 à la ligne 1 :

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dfcdcb586eed87861b3ac0ea46bea2f_l3.png)
La matrice identité a un 0 dans le dernier élément de la deuxième colonne, où il y a maintenant un 3. Il faut donc convertir le 3 en un 0. Pour ce faire, de la ligne 3 on soustrait la ligne 2 multipliée par 3 :
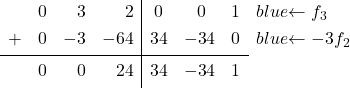
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-94ed5a1b9cf1db0bfb99ce79d0a6d36b_l3.png)
On passe à la troisième colonne : il faut transformer la dernière
![]() en un 1. Pour ce faire, on multiplie la troisième ligne par 2 :
en un 1. Pour ce faire, on multiplie la troisième ligne par 2 :
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8134938726d3b48fe3d7d789260b128_l3.png)
La matrice d’identité a un 0 dans le deuxième élément de la dernière colonne. Il faut donc convertir le
![]() en un 0. Pour ce faire, de la ligne 2 on soustrait la ligne 3 divisée par 2 :
en un 0. Pour ce faire, de la ligne 2 on soustrait la ligne 3 divisée par 2 :
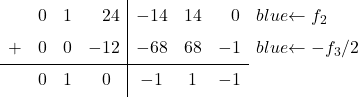
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b91b71183a50e41e9be5c7305f8cf3e_l3.png)
Il ne nous reste plus qu’à convertir le premier élément de la troisième colonne en 0. Pour ce faire, nous soustrayons la ligne 3 de la ligne 1 :

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2023374b9885dd33fe4d3c12e5a4de59_l3.png)
La matrice inverse est donc :
![Rendered by QuickLaTeX.com A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0854e7cb80ba561b6e0c724a9a9b5fff_l3.png)
Enfin, les fractions de la matrice inverse peuvent être simplifiées :
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c7ef6b6cdca2f4a808ed9457bde3b3f_l3.png)
Propriétés de la matrice inverse
La matrice inverse a les caractéristiques suivantes :
- L’inverse d’une matrice est unique .
- L’ inverse de la matrice inverse est la matrice d’origine :
![]()
- L’ inverse de la multiplication de deux matrices est égal au produit des inverses des matrices mais en changeant leur ordre.
![]()
- Transposer une matrice puis faire l’inverse de la matrice revient à faire d’abord l’inversion de la matrice puis à la transposer.
![]()
- Pour résoudre le déterminant de l’inverse d’une matrice on peut calculer le déterminant de la matrice puis faire son inverse, puisque les deux opérations donnent le même résultat.
![]()
Formule pour calculer rapidement l’inverse d’une matrice 2×2
Comme nous l’avons vu, toute matrice peut être inversée par la méthode des déterminants ou par la méthode de Gauss. Mais, à part, il existe aussi une formule pour trouver très rapidement l’inverse d’une matrice 2×2 :
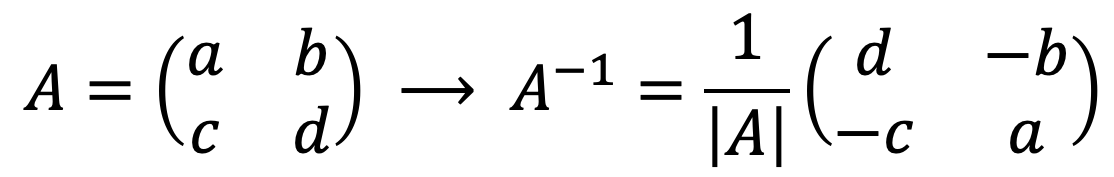
Comme vous pouvez le constater, inverser une matrice de dimension 2×2 est simple : il suffit de résoudre le déterminant de la matrice
![]() , alterner la position des éléments de la diagonale principale, et changer de signe des éléments de la diagonale secondaire.
, alterner la position des éléments de la diagonale principale, et changer de signe des éléments de la diagonale secondaire.
Exemple de comment obtenir une matrice inverse 2 × 2 avec la formule
Calculez l’inverse de la matrice carrée 2 × 2 suivante :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599baee27c05b5610a8714363e1260eb_l3.png)
Le déterminant de la matrice A est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ab99f7b87d01c670a8598df6364ab58f_l3.png)
Maintenant, nous appliquons la formule matricielle inverse :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68fd6e830b576af8abf55be1e11fbafb_l3.png)
Et on multiplie la matrice par la fraction :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41da8ef6bef1d339337717ed4ad86ae5_l3.png)
La matrice inversée A est donc :
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29da2a64f6da927857de112ca8363ba5_l3.png)
Comme vous pouvez le constater, inverser une matrice avec cette formule est beaucoup plus rapide, mais elle ne peut être utilisée que sur des matrices de dimension 2×2.
Exercices résolus de matrices inverses 2×2 avec la formule
Exercice 1
Inversez la matrice suivante de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc06e21fc1c3c54f9b3fc0dcd4912a8f_l3.png)
Le déterminant de la matrice A est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b0ae510ea7a336cbe5ea56a554da719_l3.png)
Maintenant, nous appliquons la formule pour trouver la matrice inverse :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f18178c829fd38360a04a947d52017_l3.png)
L’inverse de la matrice A est donc :
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-237fe82cd91972f667f6751fa4735534_l3.png)
Exercice 2
Calculez l’inverse de la matrice d’ordre 2 suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f2289d1c5c9aeb87016f719305d900a7_l3.png)
Le déterminant de la matrice A est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fef2cc00702131123994cc588bf7ea_l3.png)
Nous appliquons maintenant la formule pour résoudre la matrice inverse de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2de7166a0cf59e0f8c5b7750e1947f04_l3.png)
Et enfin, on fait la multiplication :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6a5973078468914beb4bd4d85a40331_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a540a077ee9a24da96fa988410aef429_l3.png)
Exercice 3
Inversez la matrice 2×2 suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36e230a808c42411a9cfd2d9eb44543d_l3.png)
Le déterminant de la matrice A est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e7a6c5ef316ae51b43c90863c6245780_l3.png)
Nous appliquons maintenant la formule pour calculer la matrice inverse de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2f359bd166c295b869a8cf04d927097_l3.png)
Et enfin, on fait le produit entre la fraction et la matrice :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a02ea2e547dcc21081ae80df407a4e0_l3.png)
Exercice 4
Trouvez l’inverse de la matrice du second ordre suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-422fcd6f391a2682e4b546c9e9c05b55_l3.png)
Le déterminant de la matrice A est :
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9997751e16d3b976454be828cb914d_l3.png)
Maintenant, nous appliquons la formule pour créer la matrice inverse de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c0c614039614bd9125b2920da8698eb_l3.png)
Et enfin, on fait la multiplication :
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb1dfc870b3045eaefc1716a80e2ca2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c49e161c701254cfbe20353c11980eb_l3.png)
Résoudre un système d’équations avec la matrice inverse
Il est difficile d’apprécier les applications réelles de l’inverse d’une matrice. En fait, vous vous demandez probablement… à quoi sert la matrice inverse ? Est-ce vraiment utilisé pour quelque chose ?
Eh bien, l’une des utilisations de la matrice inverse est la résolution de systèmes d’équations linéaires . Et oui, même si cela peut paraître comme deux concepts très différents, il est possible de trouver la solution d’un système d’équations en inversant une matrice.
Voyons avec un exemple comment cela se fait :
- Calculez la solution du système d’équations suivant avec la matrice inverse :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-200c0f994f86752e7d650621a0d4100f_l3.png)
Tout d’abord, il faut observer qu’un système d’équations peut s’exprimer sous forme de matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b9c9f181fc16a501799145c516a9747_l3.png)
On peut vérifier que cette forme matricielle du système est équivalente à l’expression avec des équations : si on multiplie les matrices on verra que l’on obtient les deux équations du système.
Maintenant, pour simplifier les prochaines étapes, nous appellerons
![]() à la matrice qui a les coefficients des inconnues,
à la matrice qui a les coefficients des inconnues,![]() à la matrice colonnes avec les inconnues, et
à la matrice colonnes avec les inconnues, et![]() à la matrice colonne avec les termes indépendants :
à la matrice colonne avec les termes indépendants :
![]()
Donc la matrice
![]() est l’inconnue de l’équation matricielle.
est l’inconnue de l’équation matricielle.
Pour résoudre cette équation matricielle, il faut suivre une procédure que nous n’expliquerons pas avec autant de détails ici. Si vous voulez le comprendre complètement, vous pouvez consulter comment résoudre des équations avec des matrices , où nous expliquons l’ensemble du processus étape par étape.
Cette procédure repose sur une propriété des matrices inverses : toute matrice multipliée par son inverse est égale à la matrice Identité (ou Unité). Par conséquent, la matrice inconnue peut être facilement résolue
![]() en multipliant les deux membres de l’équation par l’inverse de la matrice A :
en multipliant les deux membres de l’équation par l’inverse de la matrice A :
![]()
![]()
![]()
![]()
Et une fois qu’on a isolé la matrice
![]() , on calcule l’inverse de
, on calcule l’inverse de![]() et on résout le produit de matrices :
et on résout le produit de matrices :
![Rendered by QuickLaTeX.com \displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1290e37a9e3f56fc6b288bc7686d66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21471fc8a4c04aac3121519e8ef874e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9457fedf68c4bdfea898922e465eeb8_l3.png)
La solution du système d’équations est donc :
![]()