Matrice singulière ou dégénérée

Sur cette page, vous verrez ce que cela signifie pour une matrice d’être singulière ou dégénérée. De plus, nous vous montrons plusieurs exemples afin que vous n’ayez aucun doute et, enfin, nous vous expliquons toutes les propriétés de ce type de matrice.

Qu’est-ce qu’une matrice singulière ou dégénérée ?

La définition d’une matrice singulière, aussi appelée matrice dégénérée, est la suivante :

Une matrice singulière ou dégénérée est une matrice carrée qui ne peut pas être inversée et donc son déterminant est égal à 0.

Ainsi, pour savoir quand une matrice est singulière, il suffit de calculer son déterminant : si le résultat est 0, la matrice est singulière, en revanche, si le déterminant est différent de 0, la matrice est pas singulier.

Si vous souhaitez en savoir plus sur la matrice inverse, vous pouvez consulter cette page où il est expliqué en détail comment inverser une matrice par la méthode de Gauss , vous y trouverez également plusieurs exemples et exercices résolus pas à pas pour vous entraîner.

D’autre part, les matrices singulières sont également appelées matrices non régulières, car elles signifient exactement l’opposé de la matrice régulière .

Exemples de matrices singulières

Une fois que nous avons vu l’explication de la matrice singulière ou dégénérée, voyons quelques exemples de matrices singulières à plusieurs dimensions :

Exemple de matrice singulière 2×2

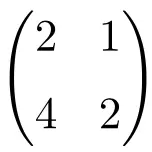
On peut facilement vérifier qu’il s’agit d’une matrice singulière en calculant son déterminant :

Le déterminant de la matrice d’ordre 2 est égal à 0, c’est donc une matrice singulière.

Exemple de matrice singulière 3 × 3

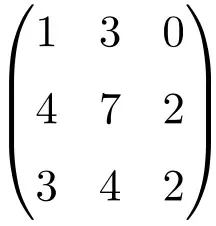
Il faut résoudre le déterminant de la matrice pour vérifier qu’il s’agit d’une matrice non inversible :

Le déterminant de la matrice d’ordre 3 donne 0, c’est donc une matrice singulière.

Exemple de matrice singulière 4 × 4

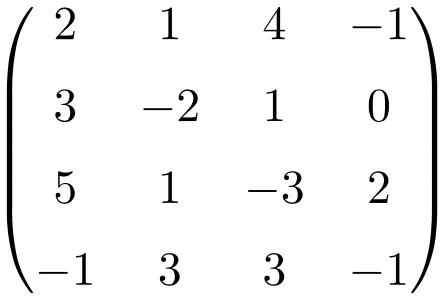
En faisant le déterminant de la matrice on montre qu’il s’agit d’une matrice singulière :

Le déterminant de la matrice d’ordre 4 est nul, donc sa matrice inverse n’existe pas.

Attention : Si vous avez des doutes sur les calculs des déterminants, vous pouvez consulter la page comment calculer un déterminant .

Propriétés des matrices singulières

Les caractéristiques de ce type de matrices sont les suivantes :

• Au moins deux colonnes ou deux lignes d’une matrice singulière sont des combinaisons linéaires et sont donc linéairement dépendantes.

• Toute matrice contenant une ligne ou une colonne remplie de zéros est une matrice singulière.

• Le rang d’une matrice singulière ou dégénérée est inférieur à sa taille.

• Le produit matriciel d’une matrice singulière multiplié par toute autre matrice donne une autre matrice singulière. Cette condition peut être déduite des propriétés des déterminants :

• De même, la puissance d’une matrice singulière est égale à une autre matrice singulière, quelle que soit la puissance à laquelle elle est élevée.

• La transposée d’une matrice singulière donne naissance à une autre matrice singulière, puisque le déterminant d’une matrice transposée (ou transposée) est équivalent au déterminant de la matrice non transposée :

• Multiplier une matrice singulière par un scalaire ne change pas son statut de matrice dégénérée.

• L’ adjoint d’une matrice singulière est aussi singulier.

• Les matrices triangulaires et les matrices diagonales sont des matrices dégénérées si au moins un élément de leur diagonale principale est nul.

• Évidemment, la matrice nulle est une matrice singulière.

• De la même manière, une matrice nilpotente est aussi une matrice singulière.

• Un système d’équations linéaires associé à une matrice singulière n’a pas de solution ou a une infinité de solutions.

• Enfin, une matrice carrée est singulière si et seulement si elle possède au moins une valeur propre (ou valeur propre) égale à 0.