▷ Comment résoudre tous types d'indéterminations (limites)

Dans cet article, nous expliquons ce qu’est une indétermination. Vous découvrirez quels sont tous les types d’indéterminations et comment les résoudre. De plus, vous pourrez voir des exercices résolus étape par étape sur les limites de fonctions de toutes les indéterminations.

Que sont les indéterminations ?

Les indéterminations, également appelées formes indéterminées, sont des expressions mathématiques qui apparaissent dans le calcul des limites de fonctions dont le résultat n’est pas défini. Ainsi, pour résoudre les indéterminations des limites, il faut appliquer une procédure préalable qui dépend du type de fonction.

Autrement dit, lorsque nous obtenons une indétermination, cela ne signifie pas que la limite n’existe pas ou qu’elle ne peut pas être résolue, mais plutôt que nous devrons apporter des modifications à la fonction afin de trouver la solution de la limite.

Types d’indéterminations

Les indéterminations, ou formes indéterminées, sont classées dans les types suivants :

Indétermination infini moins l’infini (∞-∞)
Nombre d’indétermination entre zéro (k/∞)
Zéro indétermination entre zéro (0/0)
Indétermination infinie entre l’infini (∞/∞)
Indétermination 1 élevée à l’infini (1 ^∞ )
Indétermination zéro élevée à zéro (0 ⁰ )
Zéro indétermination pour l’infini (0·∞)
Indétermination zéro élevée à l’infini (0 ^∞ )
Indétermination infinie portée à zéro (∞ ⁰ )

Nous allons ensuite voir comment résoudre tous types d’indéterminations.

Indétermination infinie moins infinie

La forme indéterminée infini moins l’infini n’est pas égale à zéro, puisqu’on soustrait deux très grands nombres mais on ne sait pas lequel est le plus grand. Le résultat de la différence des infinis dépend donc de l’ordre de chaque infini.

$\infty-\infty$

Résoudre ce type d’indétermination n’est pas facile, car selon le type de fonction, il faut appliquer une procédure ou une autre. C’est pourquoi nous vous recommandons de consulter l’intégralité de l’explication dans le lien suivant :

➤ Voir : comment résoudre l’indétermination infini moins l’infini

Nombre d’indétermination entre zéro

L’ indétermination d’une constante divisée par zéro s’obtient lorsque le dénominateur d’une fonction rationnelle est annulé.

$\cfrac{k}{0}$

Le résultat de ce type de forme indéterminée sera toujours plus infini, moins infini ou la limite de la fonction n’existera pas. Voyons comment cette indétermination est calculée en résolvant une limite à titre d’exemple :

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

Nous avons obtenu l’indétermination d’un nombre divisé par zéro, nous devons donc calculer les limites latérales de la fonction :

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ Voir : que sont les limites latérales ?

Les deux limites latérales de la fonction donnent le même résultat, donc par définition la limite de la fonction lorsque x tend vers 0 donne moins l’infini :

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

Notez que si les limites latérales avaient donné des valeurs différentes, la limite de la fonction à ce stade n’existerait pas.

Zéro entre zéro indétermination

La limite indéterminée zéro divisé par zéro est très courante et s’obtient dans des fonctions avec des fractions dans lesquelles le numérateur et le dénominateur s’annulent.

$\cfrac{0}{0}$

Ce type de limite indéterminée est résolu différemment selon la fonction. Par exemple, si la fonction a des racines, différentes étapes doivent être effectuées. Vous pouvez voir les différentes résolutions de ce type d’indétermination dans le lien suivant :

➤ Voir : comment résoudre l’indétermination zéro entre zéro

Indétermination infinie entre l’infini

L’ indétermination infinie entre l’infini se produit généralement dans les limites infinies des fonctions avec fractions. Bien que l’indétermination soit le quotient de deux infinis, le résultat ne doit pas nécessairement être l’infini.

$\cfrac{\infty}{\infty}$

Ce type de forme indéterminée est résolu par comparaison. C’est-à-dire que le degré du numérateur et le degré du dénominateur sont observés et, selon celui qui est le plus grand, le résultat de la limite est l’un ou l’autre. Vous pouvez voir tous les cas dans le lien suivant :

➤ Voir : exercices résolus sur les limites infinies entre l’infini

Indétermination 1 élevée à l’infini

Mathématiquement, on pourrait penser que 1 à l’infini donne 1, puisque toute puissance de 1 est égale à 1. Cependant, ce terme est une indétermination et, par conséquent, on ne peut pas déduire son résultat aussi facilement.

$1^{\infty}$

Ce type d’indétermination se calcule en appliquant la formule suivante :

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

Par exemple, la limite suivante est indéterminée car elle donne la puissance de l’infini :

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

Il faut donc utiliser la formule pour ce type d’indéterminations :

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

Et ainsi nous avons déjà résolu la limite indéterminée élevée à l’infini.

Zéro indétermination portée à zéro

L’indétermination zéro à la puissance zéro apparaît dans les limites de fonctions compliquées.

$0^0$

Pour résoudre ce type de limite indéterminée, il faut utiliser la propriété des limites suivante :

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Par exemple, la limite suivante donne la forme indéterminée 0 à la puissance 0 :

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

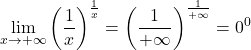
Mais si nous appliquons des logarithmes à la limite, nous pouvons trouver sa valeur :

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

Zéro indétermination pour l’infini

Il est difficile de rencontrer l’ indétermination du produit de zéro et de l’infini , mais cela ne veut pas dire qu’il est facile à déterminer.

$0\cdot \infty$

Il n’existe pas de méthode unique pour résoudre ce type d’indétermination, mais cela dépend du type de fonction. Dans ce cas, il faut transformer la fonction en l’indétermination infinie divisée par l’infini ou l’indétermination zéro divisée par zéro, et à partir de là appliquer les méthodes de résolution que nous avons vues ci-dessus pour chaque indétermination.

Donc si la limite d’une fonction est 0 et la limite de l’autre fonction est ∞ :

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

Nous pouvons transformer ce type de manière indéterminée en apportant les modifications suivantes :

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

Voyons comment procéder en résolvant une limite indéterminée à titre d’exemple :

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

On opère sur la fonction pour obtenir l’indétermination infinie sur l’infini puis on trouve la limite :

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

Indétermination zéro élevée à l’infini

L’ indétermination zéro élevé à l’infini est un peu difficile à comprendre, puisqu’on élève un très petit nombre à un très grand nombre.

$0^{\infty}$

Lorsque ces formes indéterminées sont obtenues, la formule suivante doit être utilisée :

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Résolvons un exemple pour mieux comprendre comment calculer ce type d’indéterminations :

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

Indétermination infinie portée à zéro

Normalement, toute puissance portée à zéro donne 1, cependant, l’ indétermination de l’infini portée à zéro ne doit pas nécessairement être ainsi.

$\infty^0$

Comme dans les indéterminations zéro élevé à zéro et zéro élevé à l’infini, pour résoudre ce type de limite indéterminée il faut appliquer des logarithmes :

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Voyons comment ce type de limites indéterminées est résolu en calculant un exemple étape par étape :

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

Types d’indéterminations (limites indéterminées)

Que sont les indéterminations ?

Types d’indéterminations

Indétermination infinie moins infinie

Nombre d’indétermination entre zéro

Zéro entre zéro indétermination

Indétermination infinie entre l’infini

Indétermination 1 élevée à l’infini

Zéro indétermination portée à zéro

Zéro indétermination pour l’infini

Indétermination zéro élevée à l’infini

Indétermination infinie portée à zéro

Leave a Comment Cancel Reply