Indétermination infini moins infini (∞-∞)

Dans cet article, nous expliquons comment résoudre l’indétermination infini moins infini (∞-∞). Vous trouverez des exemples de cette indétermination avec différents types de fonctions et, en plus, vous pourrez pratiquer avec des exercices résolus pas à pas de l’indétermination infini moins infini.

Résoudre l’indétermination infini moins infini

Lorsque la limite d’une fonction donne l’infini moins l’infini, cela signifie qu’il s’agit d’une indétermination (ou d’une forme indéterminée). C’est-à-dire que la limite d’une fonction qui donne à l’indétermination l’infini moins l’infini ne peut pas être déterminée en effectuant le calcul direct, mais une procédure préalable doit plutôt être effectuée.

Par conséquent, pour résoudre l’indétermination infini moins infini, il faut d’abord appliquer une procédure qui dépend du type de fonction : si c’est une fonction polynomiale, elle peut être calculée par comparaison, si c’est une fonction rationnelle, les fractions doivent être réduites à un dénominateur commun, et s’il s’agit d’une fonction irrationnelle, elle doit être multipliée par le conjugué.

\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty

Ensuite, nous allons voir avec des exemples comment l’indétermination infini moins infini est résolue dans chaque type de fonction.

Indétermination infini moins infini dans les fonctions polynomiales

Dans un polynôme, l’indétermination infini moins l’infini est égal à l’infini d’ordre le plus élevé, c’est-à-dire que le terme d’ordre le plus élevé détermine le signe positif ou négatif de l’infini.

Par exemple, regardez la limite de la fonction polynomiale suivante qui donne la forme indéterminée infini moins infini :

\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty

Dans ce cas, le terme x 2 est du second degré et le terme 3x est du premier degré, donc le monôme x 2 est dominant car il est d’ordre supérieur. Par conséquent, le résultat de la limite est l’infini obtenu à partir de ce terme.

Jetez un œil à ces autres exemples :

\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}

En bref, lorsque nous faisons des limites à l’infini dans les fonctions polynomiales , nous devons simplement substituer l’infini dans le terme de plus haut degré , en ignorant tous les autres termes.

Indétermination infini moins infini avec fractions

Lorsque l’indétermination infini moins l’infini se produit dans une addition ou une soustraction de fractions algébriques , nous devons d’abord faire l’addition ou la soustraction des fractions, puis calculer la limite.

Voyons comment calculer l’indétermination infini moins l’infini dans une fonction avec des fractions en résolvant pas à pas un exemple :

\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)

Essayons d’abord de calculer la limite :

\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}

Mais on obtient l’indétermination ∞-∞.

Donc, nous devons d’abord faire la soustraction des fractions. Pour ce faire, on réduit les fractions à un dénominateur commun, c’est-à-dire qu’on multiplie le numérateur et le dénominateur d’une fraction par le dénominateur de l’autre :

\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}

Et maintenant que les deux fractions ont le même dénominateur, nous pouvons les regrouper en une seule fraction :

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}

On opère au numérateur et au dénominateur :

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}

Et enfin, nous calculons à nouveau la limite :

\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}

Dans ce cas l’indétermination infini entre infini donne +∞ car le degré du numérateur est supérieur au degré du dénominateur.

➤ Voir : qu’est-ce que l’infini entre l’infini ?

indétermination infini moins infini avec racines

Lorsque l’ indétermination infini moins l’infini se produit dans une addition ou une soustraction de radicaux , nous devons d’abord multiplier et diviser la fonction par l’expression radicale conjuguée, puis résoudre pour la limite.

Nous allons voir comment résoudre l’indétermination infini moins infini dans une fonction irrationnelle à l’aide d’un exemple pas à pas :

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)

Essayons d’abord de résoudre la limite de la fonction avec des radicaux :

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}

Cependant, nous obtenons la forme indéterminée ∞-∞. Donc, pour savoir combien d’indétermination est l’infini moins l’infini, nous devons appliquer la procédure expliquée.

Puisque la fonction a des radicaux, nous multiplions et divisons la fonction entière par l’expression irrationnelle conjuguée :

\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}

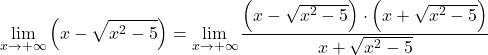
L’expression algébrique du numérateur correspond à l’identité notable du produit d’une somme par une différence, on peut donc simplifier l’expression :

\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}

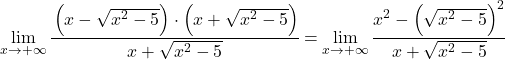
On simplifie maintenant la racine de la limite, puisqu’elle est élevée au carré :

\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}

On opère sur le numérateur de la fraction :

\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}

Et enfin, on refait le calcul de la limite :

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}

Le résultat de la limite est donc 0, car tout nombre divisé par l’infini est égal à zéro.

Problèmes résolus d’indétermination infini moins infini

Exercice 1

Résolvez la limite suivante lorsque x tend vers plus l’infini :

\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)

Dans cette limite, le terme d’ordre le plus élevé est du troisième degré, nous nous concentrons donc sur l’infini obtenu à partir de ce terme.

\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}

Exercice 2

Calculez la limite de la fonction polynomiale suivante lorsque x tend vers moins l’infini :

\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)

L’infini négatif au cube reste négatif, mais lorsqu’il est au carré, il devient positif. Bien que plus tard leurs signes soient modifiés par les coefficients devant eux :

\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}

Ensuite, la forme indéterminée infini moins l’infini est définie par le terme d’ordre le plus élevé (-5x 3 ), à partir duquel on obtient un infini positif :

\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}

Exercice 3

Déterminer la limite à l’infini de la fonction rationnelle suivante :

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)

Premièrement, nous essayons de calculer la limite en remplaçant l’infini dans la fonction :

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}

Mais on se retrouve avec l’indétermination ∞ – ∞. Par conséquent, nous réduisons les fractions à un dénominateur commun :

\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}

Et puisque les deux fractions ont maintenant le même dénominateur, nous pouvons les combiner en une seule fraction :

\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}

On fait les parenthèses du numérateur :

\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}

Et, enfin, nous déterminons la limite :

\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}

Dans ce cas l’indétermination ∞/∞ donne +∞ car le degré du numérateur est supérieur au degré du dénominateur.

Exercice 4

Résolvez la limite de la fonction fractionnaire suivante lorsque x tend vers 0 :

\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)

Nous essayons d’abord de calculer la limite comme d’habitude :

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}

Mais on obtient la forme indéterminée ∞-∞. Par conséquent, nous devons réduire les fractions de la fonction à un dénominateur commun.

Dans ce cas, x 4 est un multiple de x 2 , donc en multipliant simplement le numérateur et le dénominateur de la seconde fraction par x 2 nous obtiendrons que les deux fractions aient le même dénominateur :

\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}

Nous pouvons maintenant soustraire les deux fractions :

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}

Nous essayons de résoudre à nouveau la limite :

\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}

Mais on se retrouve avec l’indétermination d’une constante divisée par zéro. Il faut donc calculer les limites latérales de la fonction.

\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

En conclusion, puisque les deux limites latérales de la fonction au point x=0 donnent -∞, la solution de la limite est -∞ :

\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}

Exercice 5

Résolvez la limite à l’infini de la fonction suivante avec des racines :

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)

En essayant de résoudre la limite, nous obtenons l’indétermination infini moins infini :

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}

Par conséquent, puisqu’il y a des radicaux dans la fonction, nous devons la multiplier et la diviser par l’expression radicale conjuguée :

\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}

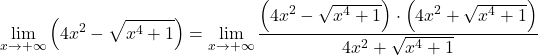
Au numérateur, nous avons le produit notable d’une somme par une différence, qui est égale à la différence des carrés. Pourtant:

\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}

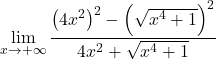
On simplifie le radical au carré :

\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}

On opère au numérateur :

\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}

Et, enfin, nous trouvons la limite :

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}

Dans ce cas l’indétermination infinie divisée par l’infini est plus infinie car le degré du numérateur est supérieur au degré du dénominateur (rappelons que la racine carrée réduit le degré par deux :

\sqrt{x^4} = x^{4/2} = x^2 ).

Exercice 6

Résolvez la limite lorsque x tend vers l’infini de la fonction irrationnelle suivante :

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)

Tout d’abord, nous essayons de calculer la limite comme d’habitude :

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}

Mais elle nous donne comme résultat l’indétermination de la différence des infinis. Par conséquent, puisque la fonction a des racines, nous devons multiplier et diviser l’expression par le radical conjugué :

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}

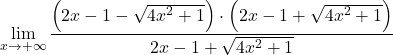
On groupe l’égalité notable du numérateur de la fraction :

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}

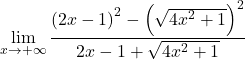
On résout la racine carrée :

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

On résout l’identité notable du carré d’une différence :

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

On opère au numérateur :

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}

\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}

Et, enfin, on calcule la valeur de la limite à l’infini :

\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =

Même s’il y a un x au carré dans le dénominateur, son degré est en fait 1 car il est à l’intérieur d’une racine :

\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .

Donc, le résultat de l’indétermination -∞/+∞ est la division des coefficients des x de plus haut degré, puisque le degré du numérateur est le même que le degré du dénominateur.

\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}

Notez que puisqu’il y a deux termes du premier degré dans le dénominateur

\bigl(2x et\sqrt{4x^2}\bigr) , pour résoudre l’indétermination -∞/+∞ il faut prendre tous les coefficients des termes du premier degré, c’est-à-dire les2 de2x et le\sqrt{4} de \sqrt{4x^2}.

Exercice 7

Calculez la limite lorsque x tend vers 1 de la fonction suivante avec des fractions :

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)

En essayant de faire la limite, nous obtenons la limite indéterminée de l’infini moins l’infini :

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}

Il faut donc réduire les fractions à un dénominateur commun, ou en d’autres termes, il faut multiplier le numérateur et le dénominateur d’une fraction par le dénominateur de l’autre :

\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}

Et puisque les deux fractions ont maintenant le même dénominateur, on peut les mettre ensemble :

\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}

Nous opérons :

\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}

\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}

Et nous essayons à nouveau de résoudre la limite :

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}

Mais on trouve l’indétermination zéro divisée par zéro. Il faut donc factoriser les polynômes numérateur et dénominateur :

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}

Maintenant, nous simplifions la fraction en supprimant le facteur qui se répète au numérateur et au dénominateur :

\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}

Et, enfin, nous résolvons la limite :

\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top